三階常系數擬線性泛函微分方程的周期解

田德生

(湖北工業大學理學院,湖北武漢 430068)

三階常系數擬線性泛函微分方程的周期解

田德生

(湖北工業大學理學院,湖北武漢 430068)

研究了一個三階泛函微分方程周期解的存在唯一性和全局吸引性:

這是一個常系數擬線性泛函微分方程.通過將這個方程轉變為三維的擬線性微分方程(組),得到了這個方程存在唯一周期解的充分條件;通過選取適當的李雅普諾夫函數,推導了這個方程解的全局吸引性;進一步,得到了此方程周期解的全局吸引性.最后,舉出了兩個應用實例.

泛函微分方程;周期解;唯一性;全局吸引性

1 引言

考慮三階泛函微分方程:

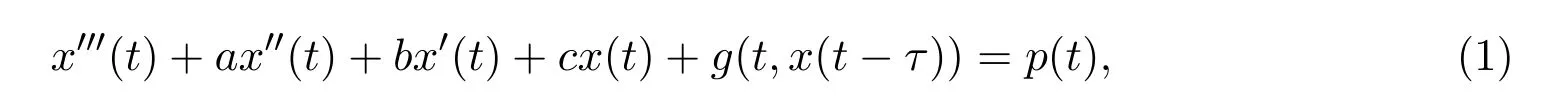
其中a,b,c,τ∈R(τ＞0)為常數;p(t)∈C(R,R)具有周期為T-函數(T為正常數); g∈C(R2,R)關于第一個變量為T-周期函數.本文研究此方程周期解的存在唯一性及全局吸引性.

近年來,三階微分方程周期解的問題得到了廣泛研究[19],所應用的研究方法也是多種多樣.文獻[1-3]對如下微分方程周期解的問題做了許多研究工作:

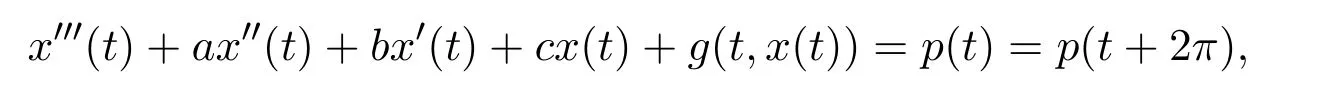
得到了方程在多種情況下周期解的存在性;文獻[4-6]應用各種不動點定理,研究了三階微分方程周期解的存在性問題;文獻[7]應用Leray-Schauder非線性選擇性原理的方法,研究了多種形式三階微分方程的周期解問題;文獻[8-9]應用重合度理論的延拓定理,分別研究了下面兩個形式的三階微分方程周期解的存在性問題:

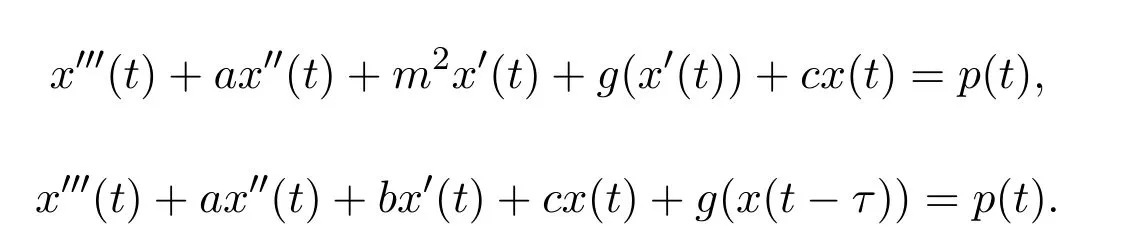
隨著人們利用計算機對微分方程解數值計算的應用和普及,越來越迫切地要求人們研究微分方程解的存在唯一性和吸引性.而且,就現有的文獻看,對三階微分方程周期解的存在唯一性和全局吸引性問題的研究成果尚不多見.因此,本文對方程(1)周期解問題的研究是十分有意義的.

目前,許多數學工作者研究了生物模型周期解的全局吸引性問題[10-12],他們的研究方法主要是選擇適當的李雅普諾夫函數,計算右上狄尼導數.本文將采用計算左上狄尼導數的方法,研究方程周期解的全局吸引性,這與他們的研究方法是不同的.一般地,計算右上導數的方法,需要估計李雅普諾夫函數的右上導數在無限區間[0,+∞)上的符號;而計算左上導數的方法,只需估計左上導數在某個有限區間[0,Ti]上的符號(詳見定理3.1的證明).因此,本文采用的計算左上導數的方法更為簡潔.

2 周期解的存在唯一性

在這一節,討論方程(1)周期解的存在唯一性.首先,介紹本文所用到的引理,它是文獻[13]中的定理3.考慮擬線性方程:

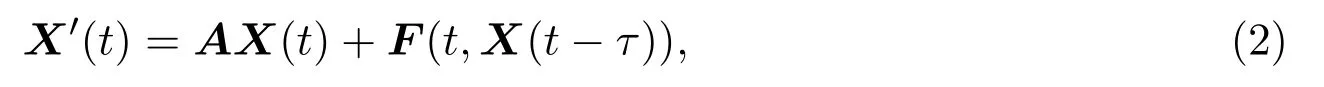
其中X∈C(R,Rn),t∈R為變量,A∈Rn×n為常數矩陣,F∈C(R×Rn,Rn)關于第一個變量為T-周期函數,τ∈R為常數.

引理2.1設T‖A‖＜2π,detA/=0,又設存在一個常數L≥0,它滿足

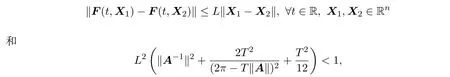
則方程(2)有唯一的T-周期解.這里,矩陣范數‖A‖是由向量范數‖X‖引導的,A∈Rn×n, X∈Rn.

在下面的討論中,約定如下的向量范數和矩陣范數:

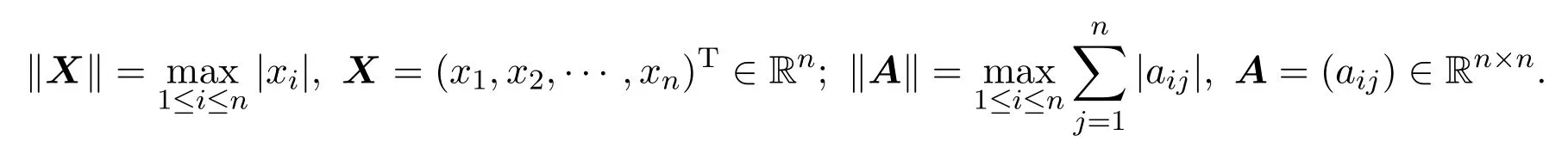
定理2.1設

(H1)存在常數L≥0,滿足

那么方程(1)有唯一的T-周期解.

證明類似于定理2.1的證明,此處略去.

3 全局吸引性

在這一節,研究方程(1)的解和周期解的全局吸引性.在這里指出,說方程(1)的一個解x?(t)是全局吸引的,如果方程(1)的其它任意解x(t)與x?(t)滿足如下的關系:

4 應用實例

最后提出:滿足定理2.1條件的周期解是否也具有全局吸引性?這將是下一步的研究工作.

致謝作者對審稿專家提出的寶貴修改意見表示真誠的感謝!

[1]Ezeilo J O C.On the existence of periodic solution of a certain third-order differential equation[J].Pro. Cambridge Philos.Soc.,1960,56:381-389.

[2]Sedziwy S.On periodic solution of a certain third-order nonlinear differential equation[J].Ann.Polon Math., 1965,17:147-154.

[3]Afuwape A U,Omari P,Zanolin F.Nonlinear perturbation of differential operators with nontrivial kernel and application to third-order periodic boundary value problems[J].J.Math.Anal.Appl.,1989,143:35-56.

[4]Chu J,Zhou Z.Positive solutions for singular non-linear third-order periodic boundary value problems[J]. Nonlinear Analysis,2006,64:1528-1542.

[5]Feng Y.On the existence and multiplicity of positive periodic solutions of a nonlinear third-order equation[J]. Appl.Math.Lett.,2009,22:1220-1224.

[6]Prasad K R,Murali P.Multiple positive solutions for nonlinear third order general three-point boundary value problems[J].Differential Equations and Dynamical Systems,2008,16:63-75.

[7]John R G,Chattanooga.Positive solutions for third order multi-point singular boundary value problems[J]. Czechoslovak Math.J.,2010,60:173-182.

[8]Zhang Z,Wang Z,Yu J.On the existence of periodic solutions of third order functional differential equations[J].Funkcialaj Ekvacioj,2000,43:461-469.

[9]Amster P,P De N′apoli,Mariani M C.Periodic solutions of a resonant third-order equation[J].Nonlinear Analysis,2005,60:399-410.

[10]Wang Q,Jizhou.Existence and attractivity of a periodic solution for a ratio-dependent Leslie system with feedback controls[J].Nonlinear Analysis:RWA,2011,12:24-33.

[11]Zhang Z,Wang H.Existence and global attractivity of positive periodic solutions for a generalized predatorprey system with time delay[J].Math.and Computer Modelling,2006,44:188-203.

[12]Li Zhong,Chen F,He M.Permanence and global attractivity of a periodic predator-prey system with mutual interference and impulses[J].Nonlinear Sci.Numer.Simulat.,2012,17:444-453.

[13]馬世旺,庾建設,王志成.擬線性泛函微分方程周期解的存在唯一性[J].數學年刊:A輯,2001,22(1):105-110.

Periodic solution of a third-order quasilinear functional differential equation with constant coefficients

Tian Desheng

(College of Sciences,Hubei University of Technology,Wuhan 430068,China)

This paper considers the existence,uniqueness and global attractivity of a periodic solution for a third-order functional differential equation:

which is a third-order quasilinear functional differential equation with constant coeffcients.By converting this equation into a three-dimensional quasilinear one,the sufficient conditions for the existence of exactly one periodic solution of this equation are established.By constructing suitable Lyapunov functionals,the global attractivity of a solution for the above equation is established;Moreover,the global attractivity of a periodic solution is established.In the last section,two examples will be provided to illustrate the applications of the results.

functional differential equation,periodic solution,uniqueness,global attractivity

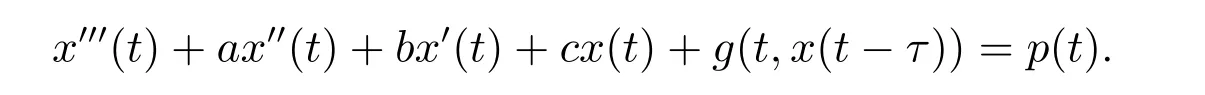
O175

A

1008-5513(2013)03-0233-08

10.3969/j.issn.1008-5513.2013.03.003

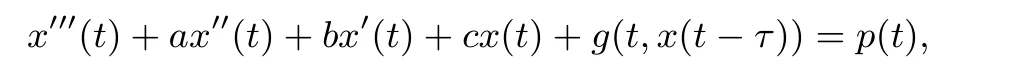
2013-03-18.

田德生(1966-),博士,教授,研究方向:常微分方程理論及其應用,生物數學.

2010 MSC:34K13