渦扇發動機進氣畸變容限控制研究

葉巍，祝劍虹，肖大啟，車杰先，任雄

渦扇發動機進氣畸變容限控制研究

葉巍1，祝劍虹2，肖大啟1，車杰先1，任雄1

(1.中國燃氣渦輪研究院，四川成都610500；2.清華大學航天航空學院，北京100084)

對某型渦扇發動機風扇，建立進氣畸變下的準一維氣動穩定性分析模型。利用該模型的計算結果，訓練一個基于BP神經網絡的畸變估算模型，并嵌入到0維發動機實時仿真程序，以實現進氣畸變容限控制。結果表明：在無畸變或小畸變情況下，通過收縮噴口來提高風扇工作點挖掘發動機潛力的作用有限；放開噴口臨界面積能有效容忍高畸變指數進氣；主燃油與主控制器強烈耦合，使得其難以穩定控制風扇裕度。

航空發動機；進氣畸變容限控制；畸變指數；BP神經網絡；穩定性

1 引言

現代戰斗機的主要特征，包括高機動性/敏捷性、垂直/短距起落、隱身和超聲巡航等。在飛推綜合和矢量推進技術推動下的高機動有著極大的攻角和側滑角，垂直起降飛機的升力風扇旋渦極易被吸入發動機，為了隱身進行進氣道遮蓋或進氣道上置導致進口氣流畸變，這些都對推進系統穩定性提出了更為苛刻的要求。按傳統方法進行大畸變容忍度的預留難以發揮發動機潛力，也難以實現超聲巡航非加力推力最大化要求。為此，各國都積極開展了大量的推進系統擴穩研究。

美國早在20世紀80年代進行先進發動機控制技術論證時，就提出了包括智能控制、性能尋優控制、穩定性尋求控制、主動失速/喘振控制四個未來發動機先進控制發展方向[1，2]。其中后兩個同屬于高穩定性發動機控制(HISTEC)的范疇[3]，主動失速/喘振控制是NASA推薦的穩定性遠期方案，穩定性尋求控制是近期方案。美國已在2000年完成了畸變容限控制的飛行驗證[2，4]，目前已經用于型號；俄羅斯在RD-33上完成了類似系統的臺架試驗。要實現畸變容限控制，需具備傳感器系統、畸變估算系統和穩定性管理控制器三要素。

文獻[5]和[6]采用畸變容限控制進行了飛推綜合研究，且都采用線性的畸變指數―裕度損失(壓比損失)關系，認為畸變敏感系數為常數。這種假設對于設計轉速附近是正確的，但在實際機動飛行中，為盡快減速轉彎往往先收油門。等指向完成后又迅速推桿加速，因此高進口畸變往往與發動機非設計轉速相伴，所以有必要改進裕度損失與畸變指數的函數關系，增加轉速作為裕度損失的參變量[7]。

本文集中在畸變帶來的裕度損失估算和穩定性管理控制器上，認為進氣畸變指數已通過傳感器系統測量并計算得到；另外徑向畸變影響很小，予以忽略，只考慮周向總壓畸變；此外，這一型號雙軸渦扇發動機的大量試驗和經驗都表明，進口總壓畸變造成的失穩總首發于低壓的風扇，所以這里只研究風扇的穩定性。

2 風扇結構與級特性獲取

以某4級風扇為試驗對象，該風扇子午面示意圖如圖1所示，僅進口0級導向器(0導)角度可調。

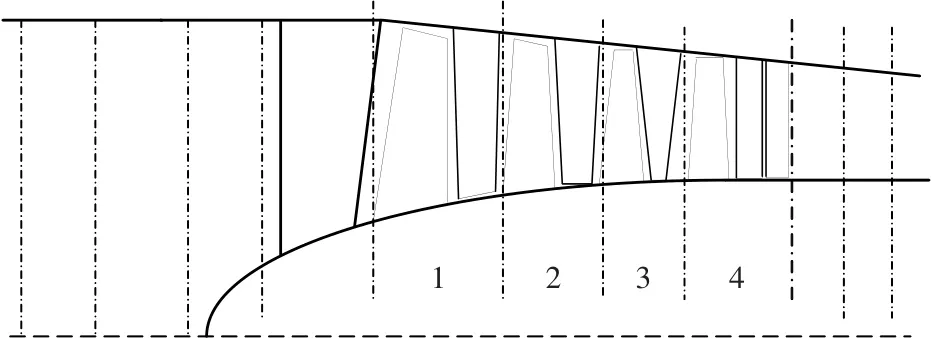
圖1 風扇子午面流道示意圖Fig.1 Meridian plane of fan

對該風扇建立準一維模型時做如下簡化：0導與進口支板簡化為一列葉片，少量厚支板簡化為與其它相同的薄支板；出口串列葉柵按文獻[8]中方法簡化為一列靜葉；不考慮風扇動葉的罩量調節。

為獲得各級特性，在設計點數據基礎上進行準一維平均半徑上的特性分解，相關方法參見文獻[9]。為校核參數和分解出的特性，用NUMECA進行了設計轉速下的單通道CFD計算。首先計算第1級，此后逐級增加，以獲取盡可能寬流量范圍的特性，最大網格數約200萬。將分解后的特性重新疊加后再與手冊數據比較，以校核分解的特性。需注意的是，該風扇前3級跨聲速，在低轉速時后面級的工況下降更為劇烈，導致第3級由跨聲速進入亞聲速，葉柵損失難以準確估算，特性誤差較大。此外，分解時采用插值方法考慮了0導實際調節計劃。

3 畸變下的穩定邊界計算

為確定畸變指數與裕度損失的關系，采用準一維激盤+改進的平行壓氣機模型，對風扇進行畸變下的穩定邊界計算。將整個風扇控制體分為10個子段，如圖1所示，每段采用圖2所示的激盤-滯后-容積模型建模。

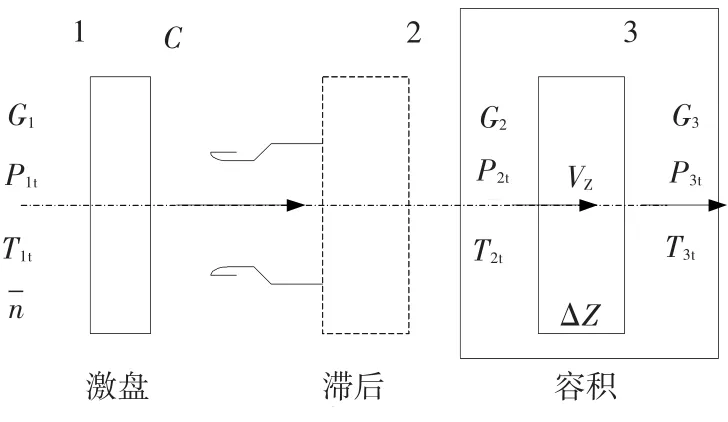
圖2 激盤-滯后-容積模型Fig.2 Actuator-lag-volume model

激盤所描述的級加功過程在級特性上插值實現；滯后環節描述子段內氣流參數對進口氣流脈動的響應，用一階滯后模型模擬；容積模塊采用一維流動集聚模型，控制體內氣流滿足質量、動量和能量守恒方程，對于無葉片段只用容積模塊，詳細的推導過程與數學模型參見文獻[10]和[11]。按進口畸變范圍，利用平行壓氣機理論，將風扇周向分為M個子壓氣機，出口利用靜壓相等進行耦合；風扇軸向分為N個子段，每子段由3個方程表達。則整個風扇的穩定性由M×N×3個方程決定。進口條件為總溫、總壓、流量，各子段初始條件由級疊加方法給定，計算中逐步減小流量以逼近失穩邊界。穩定性判別方法采用文獻[12]中的李亞普洛夫第二方法。這樣上述系統由氣動穩定性方程組求解轉化為常微分方程初邊值問題，再轉化成李亞普洛夫穩定性問題，最后變為矩陣特征值求解，用雙步長QR方法獲取特征值完成整個穩定性計算。判穩準則為：對于從初始平衡狀態出發的壓縮系統，只有在所有特征值為負的情況下才穩定。

穩定邊界計算時每1%轉速計算一個點，計算結果用設計轉速下的臨界畸變指數試驗值校核，最終結果如圖3所示，圖中W代表畸變指數。該畸變特性模擬結果與該型發動機已有畸變試驗結果吻合很好，設計轉速下的敏感系數為0.78，而該試驗值為0.65左右。將圖3所示的坐標系轉化為折合轉速—裕度損失特性，還采用畸變指數作為參變量，結果在83%～90%轉速發現一畸變敏感區，這也為試驗所證實。

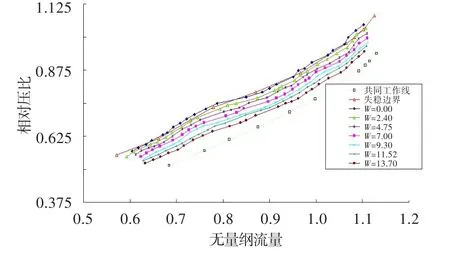
圖3 風扇總壓畸變特性Fig.3 Total pressure distortion characteristics of fan

4 主動穩定性控制方法

將上述準一維激盤模型放入工程化的進氣畸變容限控制器顯然不可取，計算工作量太大，而將上述畸變計算結果進行插值計算也較為繁瑣，且泛化能力較弱。文獻[5]和[6]采用間接參數——畸變敏感系數來表示畸變指數與裕度損失的關系，中間環節較多，且文獻中未能表達出敏感系數與折合轉速的關系。本文采用上述畸變計算結果訓練一個BP神經網絡模型，再在畸變容限控制器中對此模型輸入畸變指數和折合轉速，從而獲得裕度損失。

為將該BP神經網絡模型嵌入控制器，應盡可能簡化網絡拓撲結構與參數。這里只選用了兩層神經元，中間隱層節點數經大量試算取為10個，輸出節點1個(裕度損失)，輸入節點2個(折合轉速、畸變指數)。網絡拓撲結構如圖4所示。

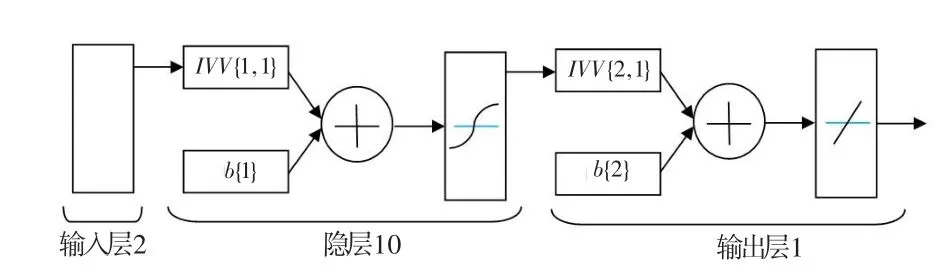
圖4 BP畸變神經網絡結構Fig.4 Structure of BP neural network

隱層激活函數采用下式的sigmoid函數：

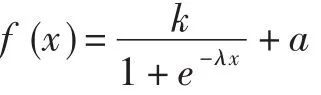
式中：陡度因子λ和縮放因子k均為2.0，位移因子a為-1，輸出層采用線性函數。整個網絡使用均方根性能函數，網絡訓練采用批處理的擬牛頓方法。需重點指出的是，本文的畸變估算模型中須采用批處理訓練方法，以避免樣本末尾某個畸變指數樣本點對權系數影響過大。

訓練樣本覆蓋從0.75～1.05折合轉速范圍共182個點(剔除明顯的失穩計算異常點)，訓練2 100步收斂，性能函數E＜0.23。BP模型計算結果與原樣本點的比較如圖5所示，其中空心圖例均為BP模擬結果。可見，相同畸變指數在風扇不同折合轉速下造成的裕度損失為非線性，因此有必要在畸變容限控制中將此非線性因素予以考慮。

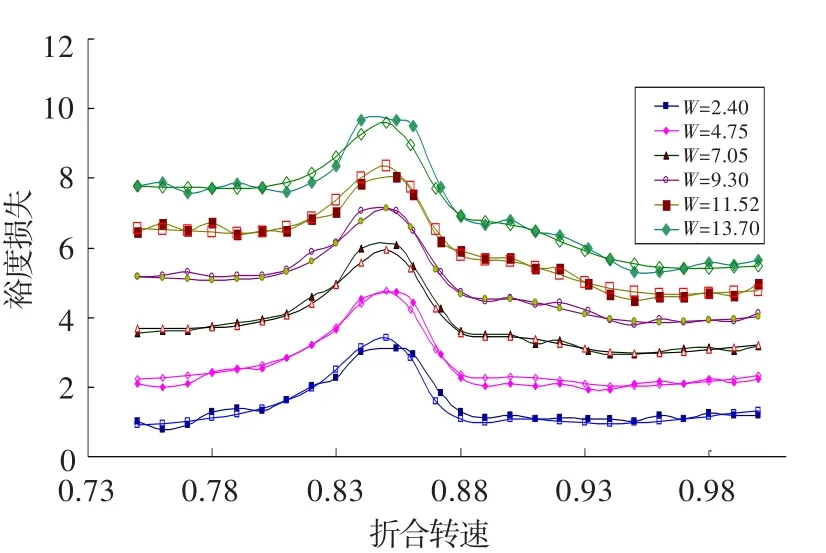
圖5 BP計算結果與原樣本點的比較Fig.5 Comparison between original samples and BP results

5 仿真結果與分析

首先確定控制目標，其次選擇控制量，最后在0維實時渦扇發動機模型中予以仿真驗證。

5.1控制目標

畸變容限控制的目的：一是想在均勻進氣的情況下將多余的裕度拿出來提升性能；二是要使發動機在超過臨界畸變指數的情況下穩定工作，實現適用范圍的擴展。

參考HISTEC，本文的控制目標為：將風扇失穩邊界(有畸變或無畸變)到共同工作線間的距離SWall(總裕度)，控制在大于內外因子畸變分界線到共同工作線的距離SWinner(裕度)的范圍內，如圖6所示。即在均勻進氣條件時提高風扇工作點來減小SWall，使之接近SWinner以發揮發動機潛力；在超過臨界畸變指數進氣時，降低風扇工作點使SWall不小于SWinner。其中內外因子畸變分界線是一條根據試驗和外場使用統計結果而人為設定的線，該線到左上側穩定邊界的距離為留給進氣畸變的可用裕度，到右下側工作線的距離為預留給其它降穩因子使用的裕度(主要是內因子)。圖中失穩邊界和工作線在畸變容限控制中都為動態變化，但SWall和SWinner都只是折合轉速的函數。

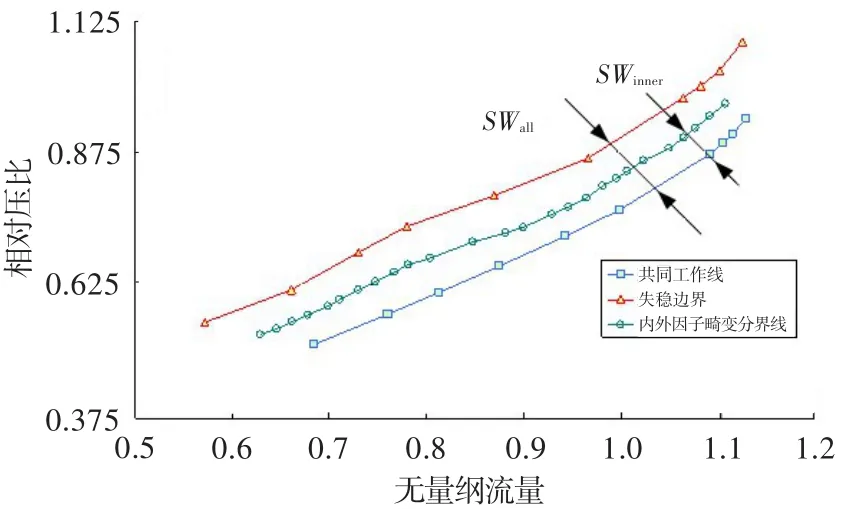
圖6 畸變容限控制目標示意圖Fig.6 The aim of distortion tolerance control

5.2控制回路選擇

考慮到實際工程應用中可供選擇的發動機調節量(噴口臨界面積A8、主燃油流量mf、風扇導葉角α1(α2)、級間放氣等)非常有限，選擇用于風扇裕度控制的標準，包括控制回路的響應速度(越快越好)、對推力的影響(越小越好)、對效率的影響(越小越好)、對主控制器的影響(越小越好)等因素。單獨調節α1易導致高低壓不匹配，且實際進氣低總壓只發生在某一周向相位，當前的0導調節器都是整周同步調節，若異步調節對控制系統改動很大，且需要實時測定低總壓區相位，這對于進口存在旋流的情況難以實現；級間放氣可用于退喘，但不適合于長時間使用以改變風扇工作點，效率影響較大。這里選擇mf和A8，但在發動機主控制器同時工作時，主控制器根據原控制計劃依然會調節包括α1在內的其它控制變量，具體控制回路如圖7所示。在原主控制回路上增加一個畸變容限控制回路，采集當前發動機進氣的畸變指數和折合轉速，用上述BP網絡計算獲取當前折合轉速下的裕度損失，根據裕度損失大小按5.1節所述控制目標發出調節mf或A8的指令。內外因子畸變分界線用插值獲取。由于缺乏非設計轉速時臨界畸變指數下裕度損失全部的試驗數據，本文利用設計轉速時臨界畸變指數造成的裕度損失百分比，將圖6中工作線到穩定邊界的距離分為兩份，以確定各轉速下要為內因子保留的裕度。

畸變容限控制器采用速度式PID控制，其中微分基本為0，因此容易造成回路過于敏感而不穩定。PID控制器輸入為SWall與SWinner間的差值，輸出為Δmf或ΔA8，將輸出疊加到主控制器輸出上以實現畸變容限控制。畸變容限控制的約束，即原發動機主控制計劃中除風扇下穩定邊界以外的全部約束。

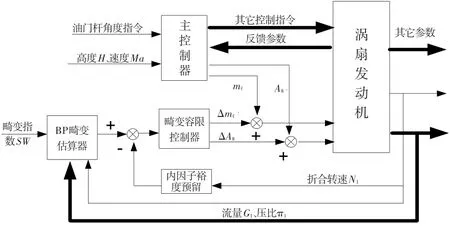
圖7 畸變容限控制回路Fig.7 The loop of distortion tolerance control

5.30維實時仿真結果

在飛行包線內選取了多個高度H和馬赫數Ma點進行仿真，這里只示出H=0 km、Ma=0的地面狀態結果，進氣畸變指數選擇3%和12%兩種狀態(該型發動機試驗獲得的設計點臨界畸變指數為10%)。在第25 s時，畸變進入發動機，設定第30 s時畸變控制器介入進行控制，第50 s畸變消失，控制器也隨之離線。

首先單獨用A8控制小進口畸變，結果如圖8所示。圖中所有參數進行了無量綱化，且相對于縱坐標進行了平移，以更清楚地顯示控制過程中發動機整體狀態參數的變化，畸變前后縱坐標之差依然是該變量的變化百分比值；下同。此時的風扇穩定裕度還有富余，因此進一步收小噴口以提高工作點發揮發動機潛力。噴口縮小約1.37%(相對最大噴口面積)，推力增加約0.56%(相對于非加力最大推力)，可見縮小噴口后裕度進一步減小，相應的mf增加以提高工作點。

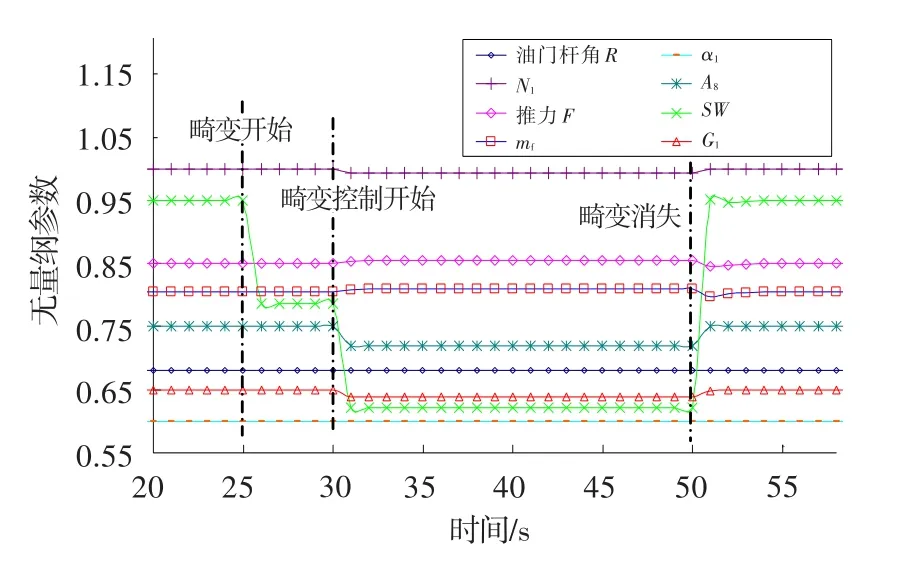
圖8 A8畸變容限控制結果Fig.8 Results fromA8distortion tolerance control

為進一步確定縮小噴口可挖掘的發動機潛力，在無畸變情況下進行了大量數值仿真，結果表明：推力增量隨噴口面積減小呈凸函數關系，起初隨著面積減小推力不斷增加，比燃油消耗量降低，推力達到峰值后急劇下降，可獲得的最大推力增量約49 daN，此時噴口面積減小2%(相對最大狀態)，最大可利用裕度為1.5%。進一步減小噴口面積導致渦輪落壓比下降后風扇獲得的功率降低，進而轉速N1降低，風扇進口流量降低，使得推力反而降低，比油耗上升，如圖9所示。因此在整機環境下，單純控制A8并不能像在部件試驗中那樣有效移動風扇工作點，也就不能進一步利用剩余裕度。

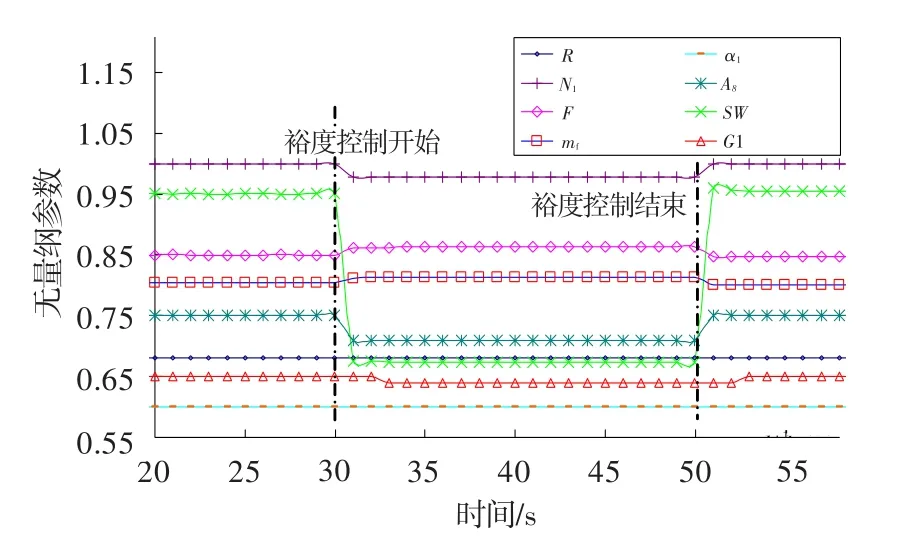
圖9 A8進一步降低裕度結果Fig.9 Further decreasing the stall margin withA8

其次在高進口畸變(W=12%)情況下，單獨用A8進行控制，結果如圖10所示。此時進口畸變已超過臨界畸變指數(Wcr=10%)。從第30 s開始，畸變控制器通過放開噴口以容忍進一步的畸變，噴口放開后壓力降低，通過外涵反饋到風扇出口，使得風扇出口背壓降低，從而達到降低風扇工作點來增大穩定裕度的目的。由于主控制器的作用，主燃油流量被降低，相應的比燃油消耗率也降低(未示出)。由于0維模型不能反映畸變后的燃燒室工作情況，所以這個比燃油消耗量并不具有參考意義。多個進氣畸變指數值的仿真結果顯示，按此畸變容限控制方法，每增加1%畸變值，推力損失約0.52%(約39 daN)。

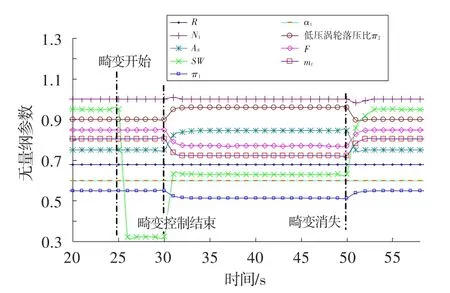
圖10 高進口畸變下容限控制結果Fig.10 Distortion control results under high inlet distortion

此外還進行了單獨用燃油流量控制裕度的仿真，但由于主控制器強烈的耦合作用，造成推力和燃油流量大幅波動，未達到預期目標，即在原主機控制方案不變的情況下，難以用主燃油流量控制裕度。HISTEC計劃采用主燃油取得了較好的畸變容限控制效果，其根本原因在于美系發動機往往采用風扇壓比-主燃油控制回路，而國內發動機和俄系發動機大都采用轉速-主燃油控制回路，后者難以用主燃油準確控制風扇的工作點，因而也就難以利用主燃油流準確控制風扇的裕度。

6 結論

(1)均勻進氣條件下，減小噴口臨界面積可提高風扇工作點，但能發揮的發動機潛力有限，因為受到渦輪落壓比回路的限制，最大可獲得49 daN左右的推力增量。

(2)在超過臨界畸變指數的情況下，用噴口臨界面積能在較小推力損失情況下有效容忍進氣畸變，但每增加1%的畸變，就有0.52%左右的推力損失。

(3)在不改變原發動機主控制器的情況下，難以用主燃油流量穩定控制風扇裕度。

[1]Adibhatla S，Brown H.Intelligent Engine Control[R]. AIAA 92-3484，1992.

[2]朱旭津.航空發動機先進控制概念和高穩定性發動機控制系統研制[J].燃氣渦輪試驗與研究，2002，15(3)：5—10.

[3]DeLaat J C，Southwick R D，Gallops G W.High Stability Engine Control(HISTEC)[R].AIAA 96-2586，1996.

[4]Southwick R D，Gallops G W，Kielb R P，et al.High Stabil?ity Engine Control(HISTEC)Flight Test Results[R].AIAA 98-37357，1998.

[5]王立峰，張津.超機動飛行推進系統穩定性控制研究[J].推進技術，2000，21(4)：1—4.

[6]郭亮.先進戰斗機的綜合飛行/推進控制系統設計與仿真研究[D].北京：北京航空航天大學，2006.

[7]胡駿.進氣畸變對軸流壓氣機性能影響實驗研究[J].航空動力學報，2001，16(2)：142—146.

[8]吳國釧.串列葉柵理論[M].北京：國防工業出版社，1996.

[9]Steinke R J.STGSTK-A Computer Code for Predicting Multistage Axial Flow Compressor Performance by a Mean?line Stage Stacking Method[R].NASA-TP-2020，1982.

[10]唐狄毅.葉輪機非定常流[M].北京：國防工業出版社，1992：235—240.

[11]喬渭陽，蔡元虎.燃氣渦輪發動機壓縮系統穩定性數值模擬的研究[J].燃氣渦輪試驗與研究，2001，14(2)：19—24.

[12]劉大響，葉培梁，胡俊，等.航空燃氣渦輪發動機穩定性設計與評定技術[M].北京：航空工業出版社，2004：214—215.

Research on the Inlet Stability Control of Turbofan Engine

YE Wei1，ZHU Jian-hong2，XIAO Da-qi1，CHE Jie-xian1，REN Xiong1
(1.China Gas Turbine Establishment，Chengdu 610500，China；2.School of Aerospace，Tsinghua University，Beijing 100084，China)

A quasi-one-dimensional model for the fan aerodynamic stability was built.Based on BP artifi?cial neural network,the results from the mode were applied on distortion estimation system.And then a 0 di?mensional real time program was embedded into the estimation system to realize the inlet distortion stability control.The results show that the potential engine margin is limited by reducing nozzle area at the uniform inlet condition.On the other hand,the engine could bear the supercritical inlet distortion when nozzle area was increased.It was very difficult to effectively control the fan stability because of the impact between the main fuel flow and the controlling unit.

aero-engine；inlet distortion control；distortion index；BP neural network；stability

V231.3

A

1672-2620(2013)05-0030-05

2013-03-27；

2013-09-09

葉巍(1968-)，男，福建長汀人，研究員，博士，主要從事發動機穩定性設計與評定研究。