基于邊光滑有限元方法的三角形單元在復合材料反對稱鋪設(shè)角層合板的自由振動分析中的應(yīng)用

李 明，李 寧，李 諍，李 威

(1.海軍駐渤船重工軍代表室，遼寧 葫蘆島125004;2.華中科技大學 船舶與海洋工程學院，武漢430074)

目前，用于復合材料層合板分析的有限元單元主要基于以下三個理論:①經(jīng)典層合板理論;②一階剪切變形理論;③高階剪切變形理論。有限元方法作為重要的數(shù)值方法被廣泛應(yīng)用，其中三角形單元以其方便的前處理和對復雜幾何形狀的適應(yīng)性，深受研究者的喜愛。然而，有限元三角形單元的發(fā)展深受精度和穩(wěn)定性低的制約。應(yīng)變光滑技術(shù)是在節(jié)點積分無網(wǎng)格方法中為得到穩(wěn)定解而提出來的［1］，很快被應(yīng)用到自然單元。針對有限元方法(FEM)“過剛”的問題［2-4］，有研究將標準有限元方法和應(yīng)變光滑技術(shù)結(jié)合起來提出的基于單元光滑的有限元方法(SFEM)和基于節(jié)點光滑的有限元方法edge-based smoothed finite element method(NSFEM)。與FEM“過剛”的特性相反，NS-FEM表現(xiàn)出“過柔”的問題，而過柔的模型也將會導致結(jié)果的不穩(wěn)定。基于邊光滑的有限元方法用于計算平面問題，表現(xiàn)出較好的性能［5］。本研究基于Mindlin一階剪切變形理論，應(yīng)用光滑有限元方法對復合材料層合板的自由振動進行分析。

1 光滑域的構(gòu)造

在光滑有限元方法中，離散域也是基于普通三角形單元。假設(shè)問題域Ω離散為N個三角形單元，問題域，這些單元網(wǎng)格共有Nn個節(jié)點和Ne條邊。將每條邊的兩個端點和這條邊相鄰的兩個三角形單元的中心相連接，這樣就在三角形單元的基礎(chǔ)上形成了Ns個基于邊的光滑域，問題域在這種情況下光滑域的數(shù)目與普通三角形單元邊的數(shù)目相等，即Ne=Ns，見圖1。

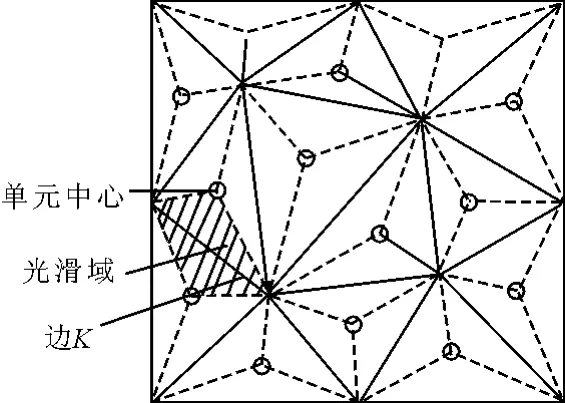
圖1 三角形單元和基于邊的光滑域

2 有限元模型

考慮一塊固定厚度為h的層合板，由一定數(shù)目的鋪設(shè)角為θ和-θ的各向異性等厚薄板交替鋪設(shè)組成，每層板的材料均為正交各向異性體。坐標系的原點在層合板的中面，z軸垂直于板中面，見圖2。

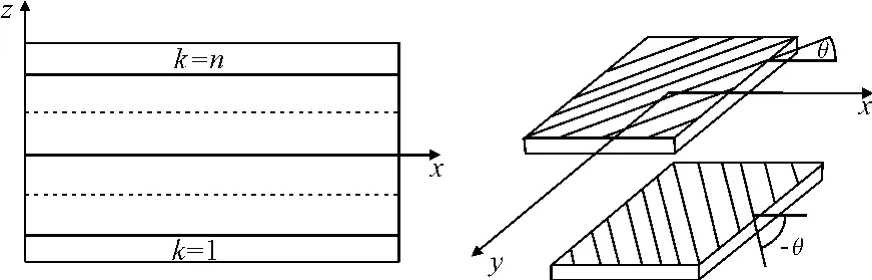
圖2 反對稱層合板示意

根據(jù)Mindlin假設(shè)，單元內(nèi)任意一點的位移可表示為

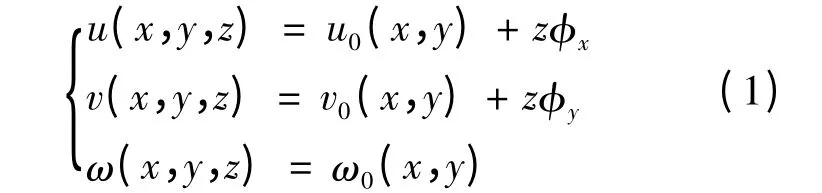
式中:u0、v0、ω0——中面上任一點的位移;

φx、φy——板變形后橫截面繞坐標軸的轉(zhuǎn)角。

線彈性位移應(yīng)變關(guān)系為

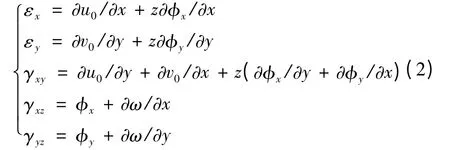
對于正交各向異性體，每一層在(x，y)平面內(nèi)的應(yīng)力-應(yīng)變關(guān)系為

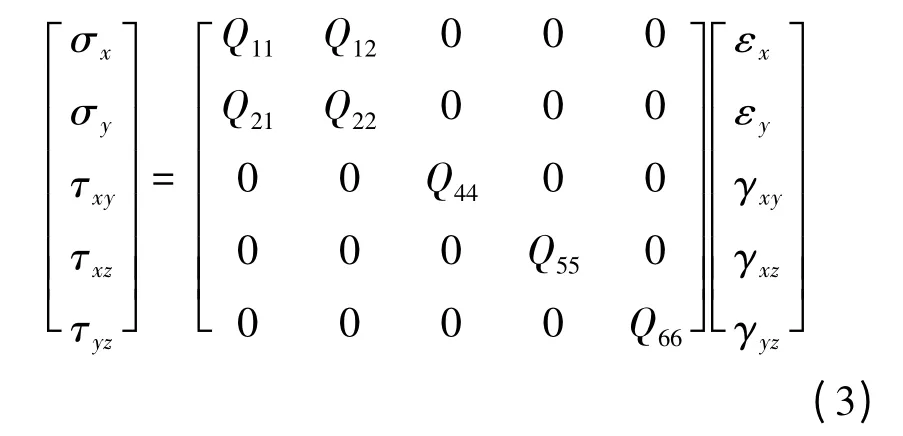
式(3)決定了層壓板各層的彈性矩陣D，它和復合材料纖維鋪設(shè)角θ有關(guān)，并且各層是不一樣的，具體見文獻［6］。

在每個鋪層內(nèi)沿z方向?qū)Ω鲬?yīng)力分量進行積分，式(2)、(3)用合力和位移的形式可表達為

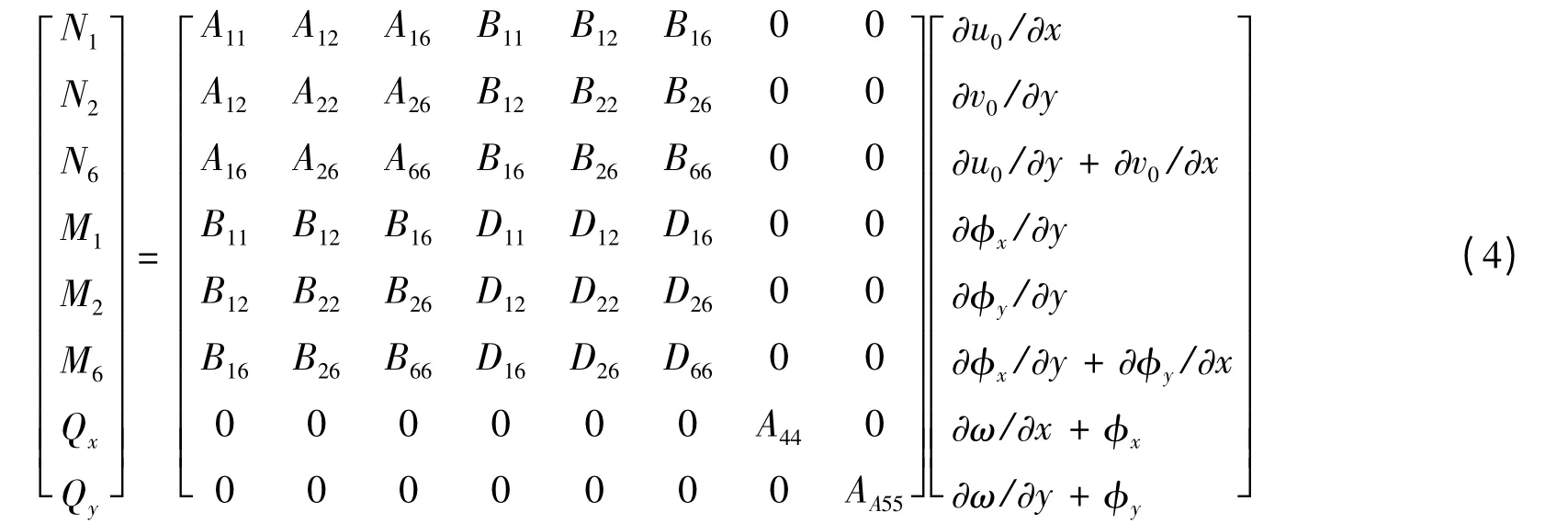
式中:

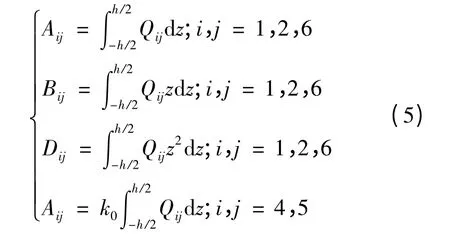
剛度系數(shù)Qij取決于該層的材料特性和鋪設(shè)角。參數(shù)k0為剪切修正系數(shù)。對于反對稱層合板，系數(shù)A16，A26，B11，B12，B22，D16和D26等于零。

根據(jù)Hamilton原理，不考慮阻尼，可得層合板自由振動的有限元控制方程:

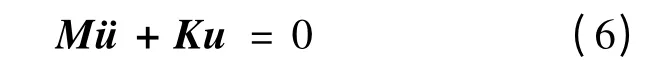
式中:M——結(jié)構(gòu)的系統(tǒng)質(zhì)量矩陣;

K——結(jié)構(gòu)的系統(tǒng)剛度矩陣;

u——系統(tǒng)的位移矢量。

單元的剛度矩陣:

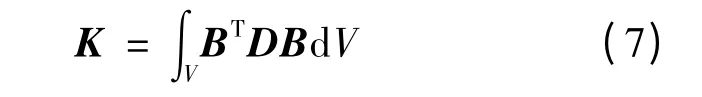
單元的質(zhì)量矩陣:

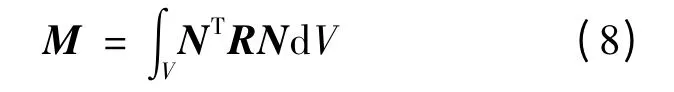
式中:B——應(yīng)變位移矩陣;

D——彈性矩陣;

N——形函數(shù)矩陣;

R——質(zhì)量密度陣。

對第k層材料有

3 剛度矩陣光滑處理

在光滑有限元方法中，光滑剛度矩陣為

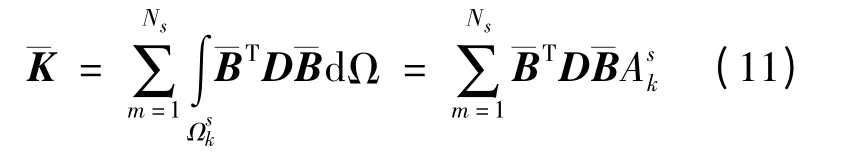
對于線性三角形單元網(wǎng)格，光滑應(yīng)變位移矩陣ˉB可以由式(12)求得:

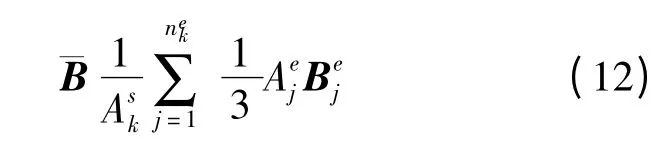
Aej———邊k周圍第j個單元的面積;

Bej———邊k周圍第j個單元的應(yīng)變位移矩陣;

Ask———邊k所在光滑域的面積，對于三角形單元:

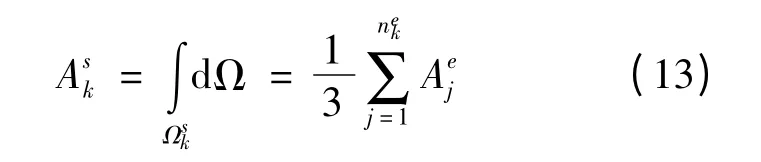
4 數(shù)值結(jié)果與討論

為了驗證光滑有限元方法的數(shù)值精度，下面分析反對稱角鋪設(shè)復合材料層合板的自由振動問題。四邊簡支矩形復合材料層合板，無量綱材料參數(shù)如下。

材料一:E1/E2=40，G12/E2=0.6，G13/E2=G23/E2=0.5，υ12=0.25;

材料二:E1/E2=25，G12/E2=0.5，G13/E2=G23/E2=0.2，υ12=0.25。

層合板無量綱一的量固有頻率

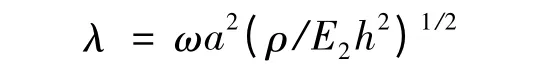
式中:ω——圓頻率;

a——層合板長;

h——板厚。

在同樣的材料，面內(nèi)位移，鋪設(shè)角和網(wǎng)格劃分等條件下用有限元方法和光滑有限元方法的計算結(jié)果見表1。層壓板材料的物理參數(shù)為:a/h=10，a/b=1，四層反對稱鋪設(shè)，例如45°/-45°/45°/-45°。用21×21節(jié)點3DOF的FEM結(jié)果作為參考值，將FEM和ES-FEM的計算結(jié)果與其進行對照，可以看出，在相同的材料、節(jié)點劃分、位移矢量和鋪設(shè)角條件下，與FEM相比，ES-FEM的數(shù)值結(jié)果更精確。很顯然，在0°～45°范圍內(nèi)，層壓板自由振動的固有頻率會隨著鋪設(shè)角的增大而增大，而隨著鋪設(shè)角的增長，固有頻率增長的速度會放緩(鋪設(shè)角為90°-θ的結(jié)果等于鋪設(shè)角為θ的結(jié)果)。三自由度(3DOF)解是通過抑制面內(nèi)位移(u，v)得到的。由表1的結(jié)果來看，在節(jié)點數(shù)比較少時，3DOF解更好一些，隨著節(jié)點越來越密集，ES-FEM的5DOF解呈現(xiàn)出更好的收斂性。但無論是3DOF還是5DOF，ES-FEM都可以得到比FEM更好的結(jié)果。

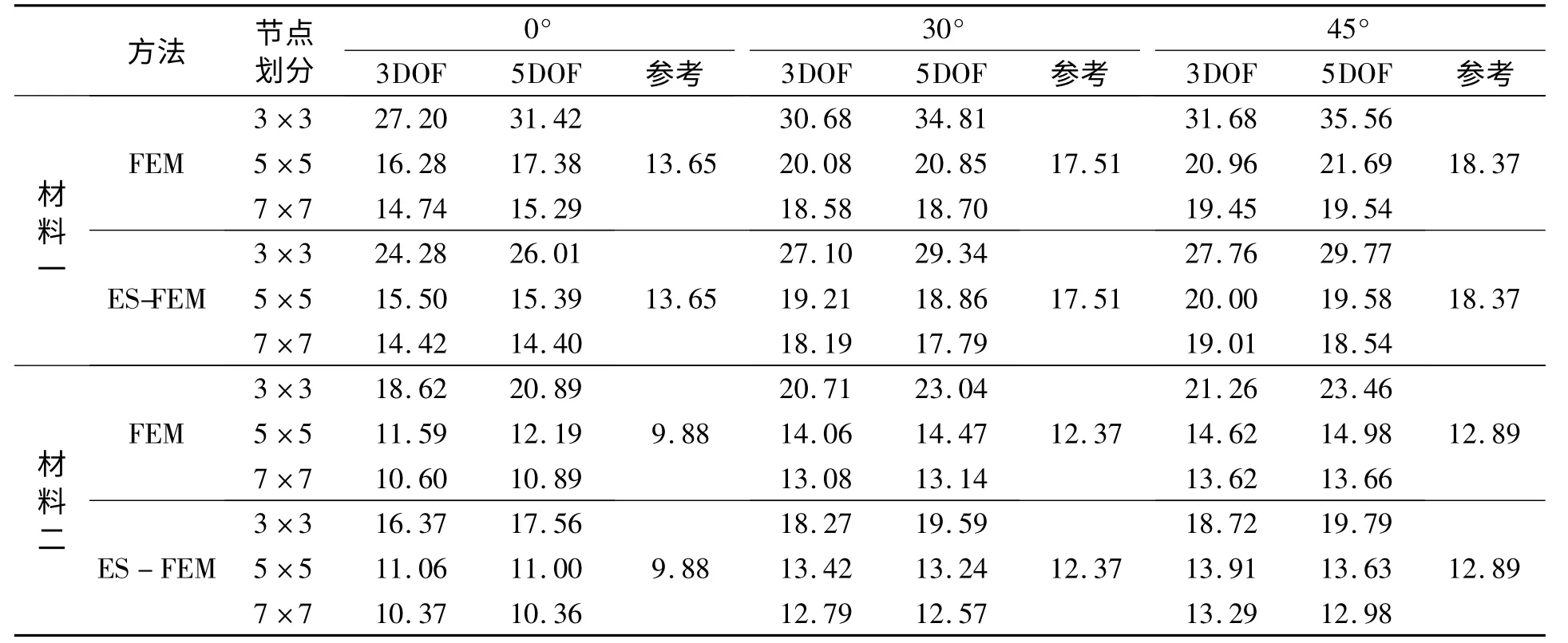
表1 層壓板面內(nèi)位移、纖維鋪設(shè)角、有限元網(wǎng)格對四邊簡支方板無量綱頻率的影響

層壓板鋪設(shè)角和鋪設(shè)層數(shù)對其無量綱基頻的影響見表2。層壓板材料的物理參數(shù)為:a/h=10，a/b=1，各鋪層間的鋪設(shè)情況為θ/-θ/θ/…/-θ。表中顯示，層壓板自由振動的基頻會隨著鋪設(shè)層數(shù)的增加而增長，而隨著鋪設(shè)層數(shù)的增加，基頻的增長會表現(xiàn)出越來越慢的趨勢。兩種方法的結(jié)果見表2。

5 結(jié)束語

本文采用邊光滑有限元方法對復合材料層合板的自由振動進行分析，簡單討論了各參數(shù)對自由振動固有頻率的影響，并將結(jié)果與標準有限元方法進行對比，結(jié)果表明:邊光滑有限元方法改善了標準有限元方法模型過剛的問題，在同樣的計算條件下結(jié)果更為精確，收斂性更好，是一種比較理想的數(shù)值計算方法。在接下來的工作中，將在以下幾個方面開展進一步的研究和討論。

1)針對更復雜的單元，例如多邊形單元和體單元，驗證光滑有限元方法的可靠性。

2)復雜邊界和任意纖維鋪設(shè)層條件下層合板的振動分析。

3)光滑有限元方法在夾層板振動和聲輻射研究中的應(yīng)用。

表2 層壓板纖維鋪設(shè)角、鋪設(shè)層數(shù)對四邊簡支方板無量綱頻率的影響

［1］CHEN JS，WU CT，YOON S，et al.A stabilized conforming nodal integration for Galerkin mesh-free methods［J］.International Journal For Numerical methods in Engineering，2001(50):435-466.

［2］LIU G R，NGUYEN T T，DAI K Y，et al.Theoretical aspects of the smoothed finite element method(SFEM)［J］.International Journal for Numerical Methods in Engineering，2007，71(8):902-930.

［3］LIU G R，DAI K Y，NGUYEN T T，et al.A smoothed finite element method for mechanics problems［J］.Computational Mechanics，2007，39(6):859-877.

［4］LIU G R.A generalized gradient smoothing technique and smoothed bilinear form for Galerkin formulation of a wide class of computational methods［J］.International Journal Of Computational Methods，2008，5(2):199-236.

［5］LIU G R，DAI K Y，NGUYEN T T.An edge-based smoothed finite element method(ES-FEM)for static，free and forced vibration analysis of solids［J］.Journal of Sound and Vibration，2009(320):1100-1130.

［6］張少實，莊 茁.復合材料與粘彈性力學［M］.北京:機械工業(yè)出版社，2005.