基于激光準直的軌道長波檢測關鍵算法的研究

王志勇,魏 暉,朱洪濤,李 靈,錢計妙

基于激光準直的軌道長波檢測關鍵算法的研究

王志勇1,2,魏 暉1,3,朱洪濤1,李 靈1,錢計妙2

(1.南昌大學機電工程學院,南昌 330031;2.江西日月明鐵道設備開發有限公司,南昌 330029; 3.江西科技學院汽車工程學院,南昌 330098)

軌道不平順是引起列車產生振動的主要原因。有資料報道,列車的激烈振動主要是軌道的長波不平順引起的。軌道長波高平順對高速列車安全、快速和舒適起關鍵性作用。目前,軌道長波不平順尚無可靠、高效的檢測手段。把激光準直技術應用到軌道長波不平順檢測是當前研究的一個方向。為減小激光準直精度對軌道長波檢測精度的影響,提出分次測量、建立測量數據二維坐標轉換模型,并對模型進行誤差分析。應用Matlab進行算法仿真,測量精度比直接測量提高了約0.19mm,表明該算法的可行性,可以應用于軌道長波不平順檢測。

高速鐵路;激光準直;長波不平順;軌道檢測;二維坐標轉換

國外在發展客運專線時發現,當列車高速(200 km/h以上)運行時會出現“1 Hz現象”[1],即車體以1 Hz左右的頻率振動加劇。如特定長度的軌道不平順對車輛產生的強迫振動頻率與車輛自振頻率接近,將導致車輛振動明顯增強,乘坐舒適性顯著降低[2]。軌道長波不平順分為軌向和高低不平順[3]。當車輛運行速度為300～350 km/h時,與車輛自振頻率接近的軌道不平順波長為83～97m。

目前,軌道長波不平順狀態檢測主要依靠基于全站儀的軌道測量儀[4],如GRP軌道檢測小車和SGJ-T軌道測量儀。但因全站儀對環境適用性差、測量效率低,故軌道測量儀用于軌道日常檢修受到很大的限制。而基于弦測法或慣性基準法[56]的GJY系列軌道檢查儀雖然具有較高的測量效率和良好的環境適應能力,然而從測量原理上講,這類儀器由于不能測量軌道外部幾何尺寸,均有一定的誤差累積,故難以對長大的長波不平順進行高精度檢測。目前,GJY-T3型0級軌道檢查儀能以2mm的重復性檢測70m波長的長波不平順。北京拉特激光的GPJ-A01軌道平順度激光檢測儀及鐵科院鐵建所JGJY激光長弦檢測儀[78],有效檢測距離≮100m,標稱檢測精度達到2mm以內,實現了長波軌向和高低偏差精密檢測,適合道岔、隧道等特殊地段和夜間作業需求。然而,該檢測儀受到結構尺寸的限制,難以滿足對曲線的長波測量的要求。

軌道長波不平順極大地影響列車安全,并加速列車車輪和軌道結構的破壞[9]。為了更好地滿足高速列車安全性和舒適性的要求,如何對各類線型準確全面地檢測出軌道長波不平順,是保證軌道高平順性的重大課題。

1 基于激光準直的長波測量系統構成

1.1 測量系統構成

系統測量原理是以激光準直技術為基礎[8],激光發射小車上的激光器發射一束準直光束,工業相機拍攝接收屏上的光斑圖像,經上位機處理獲得光斑中心坐標。光斑中心坐標的變化反映了軌道軌向和高低的狀態變化,系統如圖1所示。

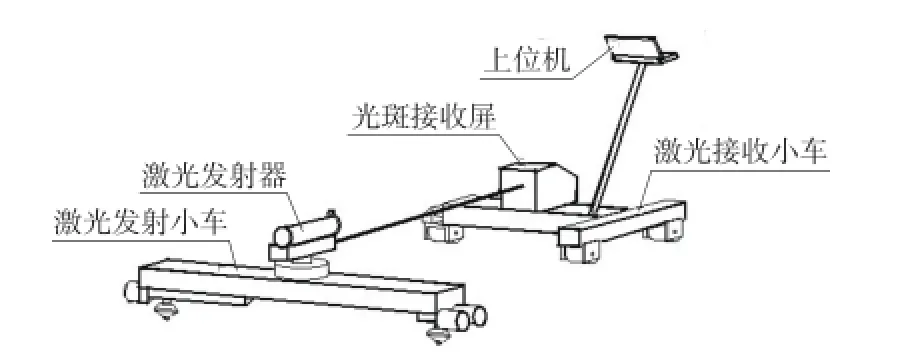
圖1 測量系統構成

1.2 激光準直測量方法簡介

測量時,固定激光發射小車,推激光接收小車前進,接收小車上的單片機系統進行數據(軌距,水平等)采集和通訊,同時工業相機采集光斑圖像,把數據和圖像傳到上位機在線處理。為了精確定位光斑中心坐標,光斑圖像處理算法綜合運用了中值濾波,自適應閥值算法,形態學濾波法和光斑重心法[10]。

激光測量方向性好,但由于激光漂移、光線彎曲和空氣擾動等原因,其準直性存在一定的誤差[1112]。在測量100、200m弦長的軌道不平順時,激光的準直精度達不到測量長度要求。激光角漂在10-4～10-5rad時,角漂對長波不平順的測量將產生不可忽視的影響。例如,系統選用10-5rad級角漂的激光準直,意味著距離激光發射點100 m處的光斑有1 mm的游移范圍。另據文獻[13],高速鐵路平面半徑Rmin=3 500 m,當對其進行150m/300m校核時,其弦矢高可達3m,即便是100m中點弦測量,其中點矢距亦可達0.35m。此即意味著,采用激光準直技術直接測量曲線軌道長波不平順,其光斑接收屏結構尺寸將達米級。綜上,激光準直測量距離就受到一定限制。

2 長波不平順檢測算法

2.1 長波不平順的激光準直分次測量

針對上述軌道檢測的技術問題,本文提出分次測量,建立測量數據坐標轉換模型,實現軌道長波的檢測。將激光發射小車在第一次測量時所在位置作為基準坐標系,通過重復測量段數據求解坐標轉換參數,把激光發射小車第2次,第3次,第n次測量坐標系數據變換到基準坐標系下,得到相對基準坐標系隨里程變化的軌向值和高低值。為了保證重復段數據配準,可以采用標記法或自適應匹配法。

由于高程坐標與平面坐標正交,故僅以測量軌向為例進行說明。如圖2所示,對曲線P1P(n進行平面測量。當測距l里程間隔較遠時,首先置激光發射小車于測量起始點P1,瞄準后推行激光接收小車至C2,采集P1至C2的軌道平面數據。此時,以激光弦l1為x軸,建立基準坐標系{O;x,y};之后,將激光發射小車移動至P2點,接收小車再往回推行到C1處,瞄準后推行激光接收小車至C3采集C1至C3的軌道平面數據,其中C1C2是搭接測量段。此時以激光弦l2為x(1)軸,建立獨立坐標系{O(1);x(1),y(1)};相應,移動激光發射小車于P3、P4、…,分別測量C3C5、C4C6、…數據,其中C3C4,C5C6是搭接段。

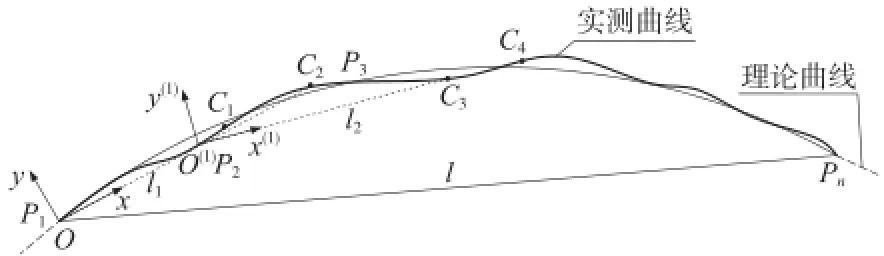
圖2 軌向測量原理

2.2 長波不平順檢測算法模型

設{O;x,y}和{O(1);x(1),y(1)}為平面內的兩個坐標系,橫坐標是里程,縱坐標是軌向或高低值,如圖3所示。

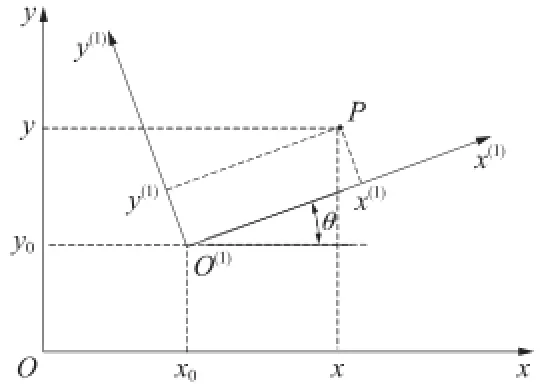
圖3 坐標系轉換示意

設P是平面內任意一點,在坐標系{O;x,y}和{O(1);x(1),y(1)}的測得數據分別為(x,y)與(x(1), y(1)),O(1)點在坐標系{O;x,y}中的坐標為(x0,y0)。由平面直角坐標變換公式得

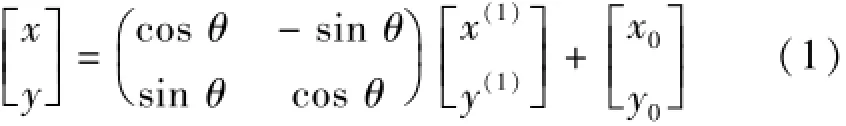
由式(1),可解得兩坐標系的旋轉角θ

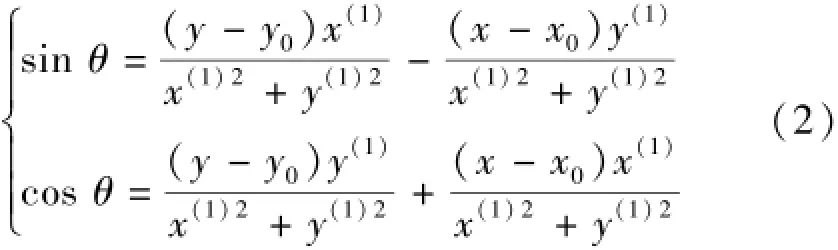
設重復測量段有N組數據,i∈N,對cosθ,sinθ取殘差有(殘差方程式)

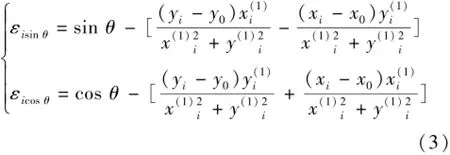
當測量誤差無偏、正態獨立條件下,求其算術平均可得估計量的最可信賴值。設在全量程內取N個標定點,由式(3),有

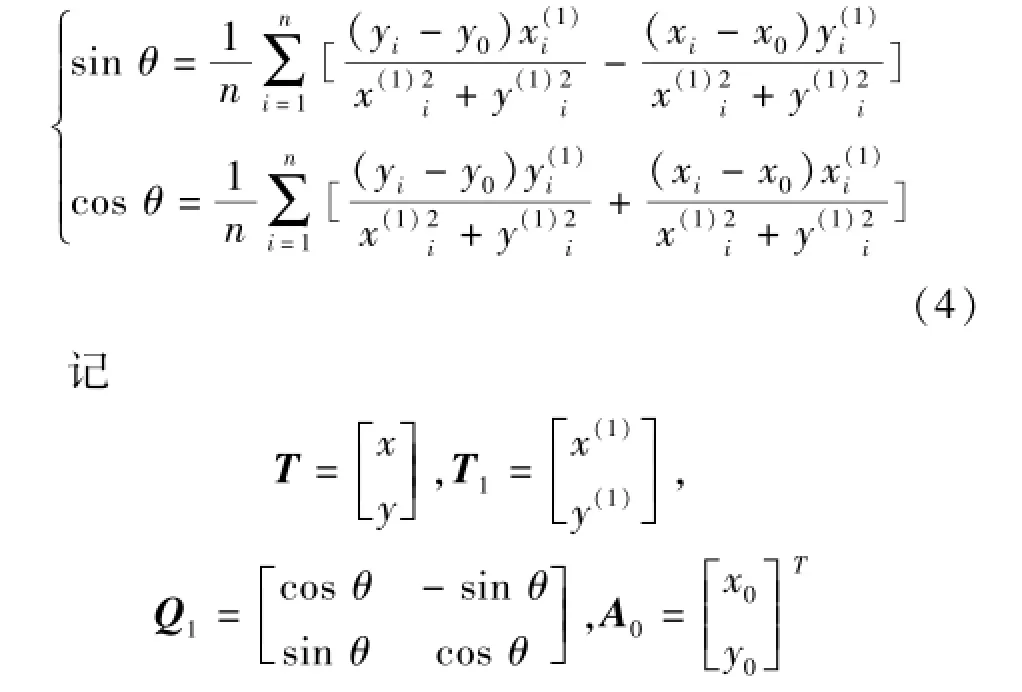
則式(1)可寫成矩陣形式

設進行平面坐標系{O(M);x(M),y(M)}到{O(M-1); x(M-1),y(M-1)}坐標變換,則旋轉矩陣

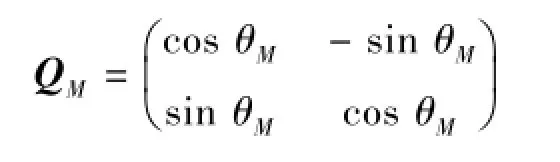
M=1,2,…,k,…,θM是第M個坐標系與第M-1個坐標系之間的轉向角。QM為{O(M);x(M),y(M)}到{O(M-1);x(M-1),y(M-1)}的旋轉矩陣;TM=[x(M), y(M)]T,TM為測量數據在平面坐標系{O(M);x(M), y(M)}中的坐標值;AM-1=[x(M-1)0,y(M-1)0]T,AM-1為平面坐標系{O(M);x(M),y(M)}坐標原點在{O(M-1);x(M-1), y(M-1)}中的平移向量。

把每段激光弦長的數據坐標值轉化為前一段弦長所在坐標系,有

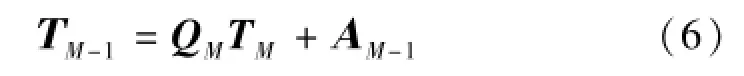
圖2所示,可將各獨立坐標系{O(M);x(M),y(M)}下的短波測量數據按式(6)變換為基準坐標系{O;x, y}下的長波測量數據。坐標轉換關系可表達為

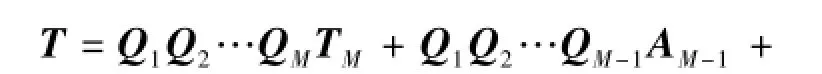
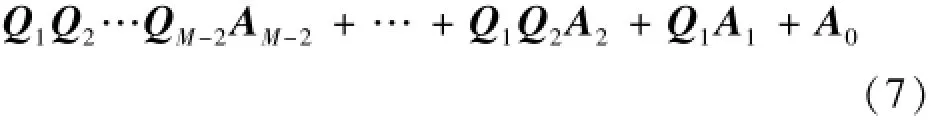
3 算法誤差分析

通過式(7)進行坐標轉換,得到在基準坐標系{O; x,y}下的軌道平面曲線,即可依據文獻[13]進行軌道平順性評價,但顯然式(7)引入的誤差將隨著M的增加而顯著增加,故應限制檢測波長。在列車運行速度350 km/h,列車敏感的不平順波長≯150 m。當設站距離60m、搭接段長度20 m的條件下,最多需要3次坐標轉換即可滿足要求,故一般情況下M≤3。由于QM是用最小二乘法原理求出的,總是存在誤差,設其誤差為ε(QM)。以M=3為例分析算法誤差。由式(7)得

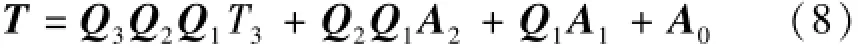
根據多元函數的誤差計算公式,得誤差ε(T)為

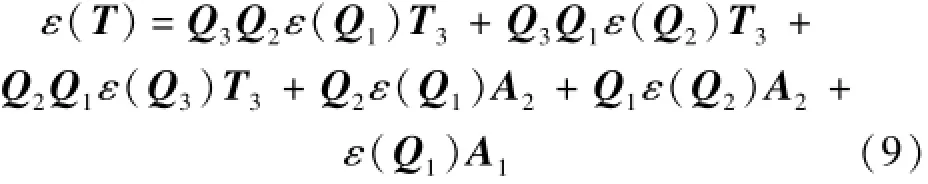
以扣件節點0.625m間距計算,搭接點數N=33。在此條件下,sinθ、cosθ的中誤差約為直接計算的1/6。隨著搭接段長度的增加,搭接精度將逐漸提高,但計算量也將顯著增加。故一般條件下,搭接段長度取20m。

4 算法仿真

為了驗證算法,以測量弦長l=100 m,R=7 000m的圓曲線的軌向平順性為例,分兩次測量,第一次測量60m,第二次測量60m,實現100m弦長的測量。利用Matlab生成軌道自身不平順和激光角漂誤差數據,如圖4所示。里程40～60m為重復段測量數據。

圖4 仿真測量數據

利用本文算法,計算旋轉矩陣結果如表1所示。把第二次測量數據轉換到第一次測量坐標系,得100m弦測量值如圖5所示。

表1 計算結果

算法誤差分析,由表1得坐標系轉換均值誤差

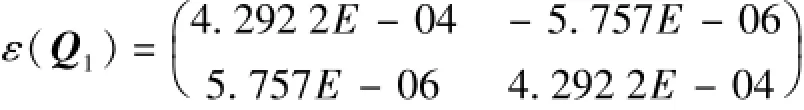
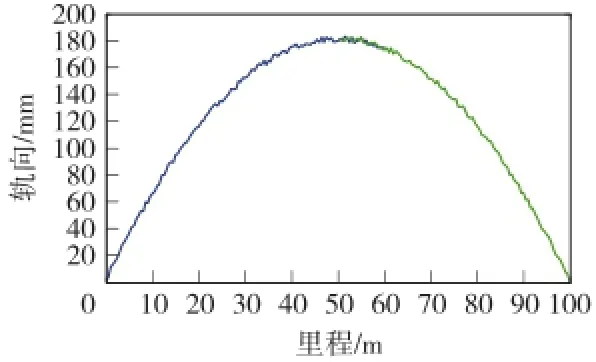
圖5 100 m弦軌向測量值

代入式(7),坐標轉換產生的最大里程誤差εx為21.462 2 mm,最大軌向誤差εy為0.210 5 mm。因此,本算法計算的軌向不平順最大誤差為

ε=60 000×10-5+ε2=0.810 5mm＜1mm

5 結語

本文分析了當前高速鐵路軌道長波檢測儀器的現狀,研究了基于激光準直技術的軌道長波檢測儀。針對長距離激光準直精度不夠問題和光斑接收屏限制,建立了多次測量坐標轉換模型,并對算法進行了誤差分析和仿真計算,根據仿真的結果,軌向測量精度比直接測量提高了約0.19 mm,可以應用于軌道長波不平順檢測。

本文提出的多次測量數據拼接模型不僅可以運用于鐵路軌道,還可運用于電梯導軌、起重機軌道等直線度檢測的數據處理。

[1] 羅林.高速鐵路軌道必須具有高平順性[J].中國鐵路,2000(9): 8- 11.

[2] 王開云,翟婉明,劉建新,等.線路不平順波長對提速列車橫向舒適性影響[J].交通運輸工程學報,2007,7(1):1- 5.

[3] 翟婉明.車輛—軌道耦合動力學[M].2版.北京:中國鐵道出版社,2001.

[4] 王成.無砟軌道平順性控制技術探討[J].鐵道標準設計,2009 (S1):57- 59.

[5] ESVELD C.Principles of track quality recording and assessment[J]. Rail International,1992,18(1):10- 18.

[6] 杜鶴亭.長波長軌道不平順檢測中的數字濾波方法[J].中國鐵道科學,2000,21(4):58- 65.

[7] 劉洪云,王彥春,王培昌,等.GPJ-A01軌道平順度激光檢測儀[Z].北京:通州區科委,2010.

[8] 高春雷,王發燈.利用激光準直技術檢測線路的長波不平順[J].鐵道建筑,2009(1):81- 85.

[9] 練松良,黃俊飛.客貨共運線路軌道不平順不利波長的分析研究[J].鐵道學報,2004,26(2):111- 115.

[10]Gonzalez R C,Woods R E.數字圖象處理[M].2版.阮秋琦,阮宇智,譯.北京:電子工業出版社,2007.

[11]方仲彥,殷純永,梁晉文.高精度激光準直技術的研究(一)[J].航空計測技術,1997,17(1):3- 6.

[12]方仲彥,殷純永,梁晉文.高精度激光準直技術的研究(二)[J].航空計測技術,1997,17(2):5- 8.

[13]中華人民共和國鐵道部.TB 10621—2009高速鐵路設計規范[S].北京:中國鐵道出版社,2009.

Study on Key Algorithm of Track Long W ave Detection Based on Laser A lignm ent

WANG Zhi-yong,WEIHui,ZHU Hong-tao,LILing,QIAN Ji-miao
(1.School of Mechatronics Engineering,Nanchang University,Nanchan 330031,China; 2.Jiangxi Everbright Railway Equipment Development Co.,Ltd.,Nanchang330029,China; 3.School of Automotive engineering,Jiangxi University of Technology,Nanchang 330098,China)

Track irregularity is the principal factor which gives rise to vibration of train.It has been reported that the violent vibration of train is caused by long wave irregularity of track.That is,the long wave regularity plays a critical role in safety,speediness and ride com fort of high-speed train.Atpresent,however,there is no reliable and efficientmanner for the detection of long wave irregularities of track.So,it is a current research direction to introduce laser alignment technology into long wave irregularity detection of track.In order to weaken the unfavorable effect on long wave irregularity detection accuracy caused by laser alignment accuracy,a fractionated measurement method was proposed,two-dimensional coordinate transformationmode ofmeasure data was established in this paper, and error analysis of the mode was carried out.Afterwards,the results of algorithm simulation using Matlab show that,the accuracy of this algorithm is about 0.19 mm higher than that of traditional algorithm,that is to say,this algorithm is feasible and can be used in long wave irregularity detection of the track.

high-speed railway;laser alignment;long wave irregularity;track detection;twodimensional coordinate transformation

U216.3

A

1004- 2954(2013)07- 0012- 04

2012- 12- 06;

2012- 12- 14

江西省科技支撐項目(編號:20111102040100)

王志勇(1973—),男,講師,工學碩士,博士研究生,E-mail: wzy_ncu@163.com。