聚合物驅流線模擬中的更新流線問題

湯昌福，王曉冬，劉翰林，王軍磊

(1.中國地質大學(北京)，北京 100083;2.中石油勘探開發研究院，北京 100083)

引 言

聚合物作為提高采收率技術的主要手段之一，已經在礦場實踐中得到廣泛應用［1－3］。聚合物驅過程本身是1個復雜的過程，同時考慮到礦場條件的復雜性，大多數情形下聚合物驅都需要借助于數值方法進行研究［4－7］，聚合物驅數值模擬方法的發展對聚合物驅項目的成功實施至關重要。

近年來，油藏流線模擬技術獲得了快速發展，并已經在提高采收率技術預測中得到推廣和應用［8－9］。油藏流線模擬具有直觀、計算速度快、數值耗散小等優點。Patton等人［4］在1971年就運用流線方法研究了聚合物驅過程，不過在研究過程中忽略了驅替過程中流場的變化，模擬過程中并未對流線進行更新。隨著流線模擬方法的發展，流線更新方法逐漸在油藏流線模擬中得到應用［8－9］。Thiele等人［5］于近期將該方法應用到聚合物流線模擬中，同時還運用自適應隱式方法求解了飽和度方程和聚合物濃度方程。

近年來，中國油藏流線模擬技術也獲得了快速發展。姚軍等人［10］提出了流線數值試井方法;侯建等人［6］結合邊界元方法，運用流線方法研究了任意不規則邊界情形下聚合物驅替過程。然而，其研究都是基于固定流線的假設下實施的，模擬過程中流線未進行更新;當驅替過程中流體流度差異較大或生產制度發生變化時，固定流線方法會造成較大誤差［11］。

本文運用流線方法研究平面聚合物驅過程，計算中考慮了流線更新對模擬結果的影響，通過更新流線來描述驅替過程中的流場的變化;同時，為提高流線方法的精確性，采用了高階精度差分方法求解飽和度方程和聚合物濃度方程。

1 數學模型

聚合物驅主要通過提高水相黏度、減小驅替過程流度比、提高波及系數等方法，從而提高采收率;驅替過程中還伴有巖石吸附效應、水相滲透率下降、剪切稀化、存在不可及體積等現象。本文采用1種聚合物驅流線模擬方法，考察流線更新對聚合物驅過程的影響，為簡單起見，只考慮了聚合物驅過程中黏度變化以及巖石吸附2個因素，其他因素如滲透率下降、剪切稀化等可以在模型中增加相關參數進行研究，具體可以參考文獻［5－6］。本文聚合物模型主要基于以下假設。

(1)驅替過程為不可壓縮等溫達西滲流過程，不考慮重力和毛管力對驅替過程的影響。

(2)油水兩相流動，聚合物僅溶于水中，聚合物的存在對水相連續方程沒有影響。

(3)不考慮剪切作用對黏度的影響，水相黏度僅僅是聚合物濃度的函數，可以表示為:

式中:μw為水相黏度，mPa·s;μwpure為純水黏度，mPa·s;C為聚合物濃度，kg/m3;H(C)為關于聚合物濃度的多項式，可以通過表格輸入。

(4)驅替過程中發生等溫吸附過程，吸附濃度可以用Langmuir吸附等溫線表示［6］:

式中:Ca為吸附濃度，kg/kg;a，b為Langmuir吸附常數，m3/kg。

聚合物驅過程需滿足水相連續方程和聚合物濃度連續方程［4－5］。水相連續方程為:

聚合物濃度連續方程為:

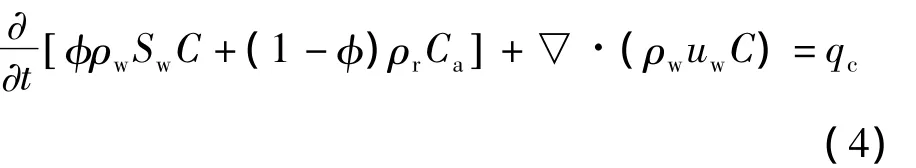
式中:下標n=w，o，分別為水相和油相;S為飽和度;φ為孔隙度;ρ為相密度，kg/m3;ρr為巖石密度，kg/m3;q為源匯項;u為相滲流速度，m/s，滿足達西公式:

式中:K為地層滲透率，10－3μm2;Kr為相對滲透率;pn為相壓力，MPa;不考慮毛管力時，油相和水相壓力相等，設p=pw=po。

2 控制方程

定義總速度為ut=uw+uo，由不可壓縮流體假設，得到:

油相和水相方程相加消去飽和度，得到聚合物驅過程壓力方程為:

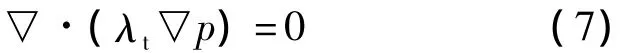
式中:λt為總流度，等于油相流度和水相流度之和。

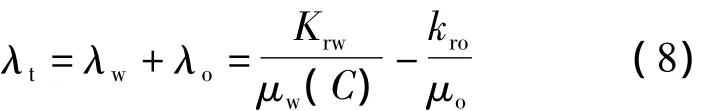
定義流線為s，其切線方向與速度方向一致的曲線［8］，得到:

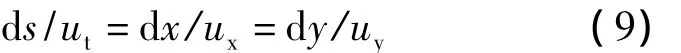
進一步定義沿流線傳播時間τ，得到:

利用式(6)得到，水相連續方程和聚合物濃度方程沿流線方向的方程:

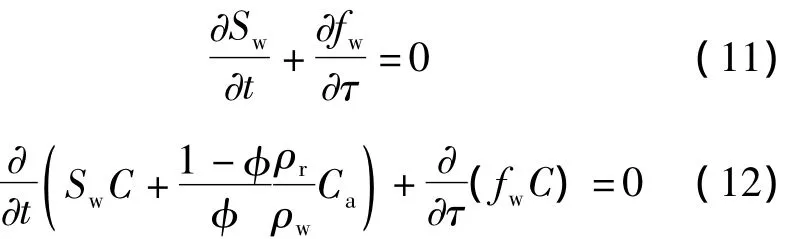
式中:fw為水相分流量，fw=λw/(λw+λo)。

根據以上分析表明，流線方法將二維(或三維)飽和度和聚合物濃度方程轉換為沿流線一維物質輸送方程，降低了求解難度。因此，驅替過程的計算可以先沿流線一維進行，然后匯總各流線結果即可。

3 求解方法

聚合物驅流線模擬過程主要包括:①運用IMPES方法求解壓力方程(7);②根據 Pollock方法［10］追蹤流線;③為提高計算精度，減小數值耗散，采用顯式全變差遞減(TVD)差分格式求解飽和度方程(11)和濃度方程(12);④進行流線更新。

4 計算實例

圖1 油水相對滲透率曲線

為了分析流線更新及其影響，模擬了平面五點井網聚合物驅過程，并和Eclipse軟件進行對比。其中，地質模型參數為:①二維平面均質地層，考慮到對稱性，取五點井網的1/4作為研究對象(一注一采情形);②地層滲透率為 300 ×10－3μm2，孔隙度為0.2;③等流量生產，注入和采出流量均為20 m3/d，純水黏度為1 mPa·s，油相黏度為8 mPa·s;④水相密度為1 000 kg/m3，油相密度為800 kg/m3，巖石密度為2 300 kg/m3。油水兩相相對滲透率曲線如圖1所示;水相黏度和聚合物吸附濃度隨聚合物濃度變化曲線如圖2。

圖2 聚合物水相黏度變化曲線和吸附曲線

聚合物驅具體實施過程為:注入1.43 PV水后轉為聚合物驅，注入濃度為1 kg/m3的聚合物溶液。圖3為聚合物驅含水率曲線fw、生產井聚合物采出濃度Cp以及采出程度η隨注入孔隙體積的變化關系曲線。約注入2.29 PV時生產井含水率開始下降，且生產井見聚合物;之后逐漸形成含水率曲線“下降漏斗”，含水率約在2.67 PV時降到最小;最終生產井含水率為98%時采出程度約為0.42 PV，而同期水驅采出程度為0.38 PV，采出程度提高了10.5%。其中，圖3中還給出了Eclipse軟件的計算結果，可以發現兩者的結果相近，驗證了流線方法的有效性。

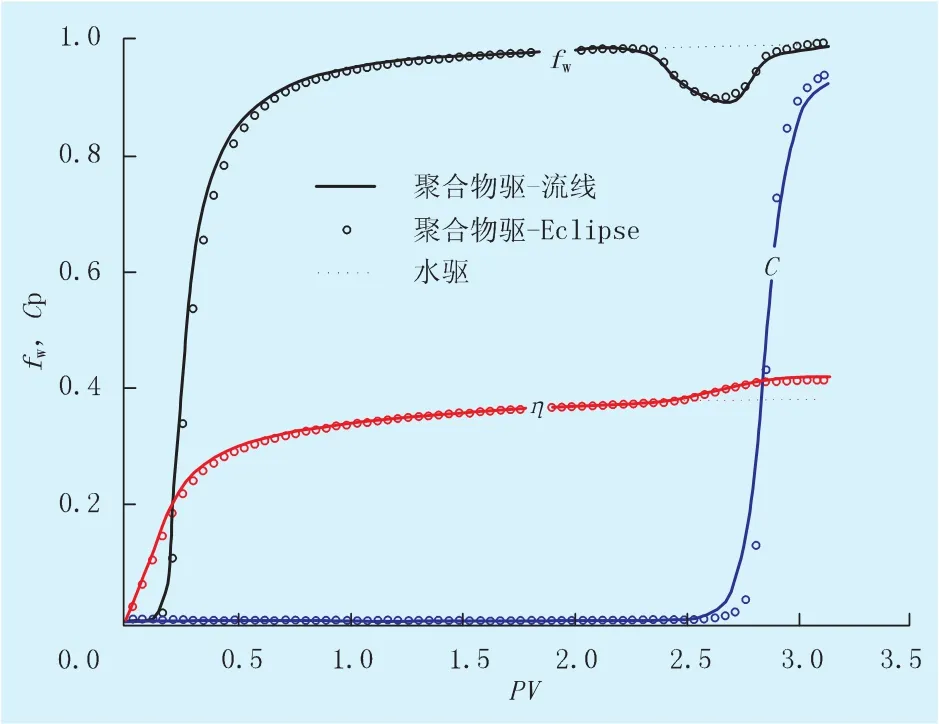
圖3 聚合物驅動態曲線

此外，進一步考察了流線更新對聚合物驅流線模擬結果的影響，圖4為固定流線和更新流線時聚合物驅模擬結果。可以發現，在水驅階段，兩者吻合較好，固定流線的假設是合理的;然而，轉入聚驅階段后，固定流線方法出現了較大誤差，其含水率“下降漏斗”和生產井采出濃度曲線與更新流線方法得到的結果相差較大。正如Martin和Wegner在文獻［9］中所指出的:對于不利驅替過程，流度的變化對流場的影響很小，固定流線的假設是合理的;對于有利驅替過程，其流場隨著驅替過程的進行變化很大，不更新流線會引起較大的誤差。在聚合物驅過程中，前期水驅為不利驅替過程，而轉為聚驅后，由于水相黏度的增加，驅替變為有利驅替過程。因此，固定流線方法在水驅階段的誤差較小，而聚驅階段的誤差較大。

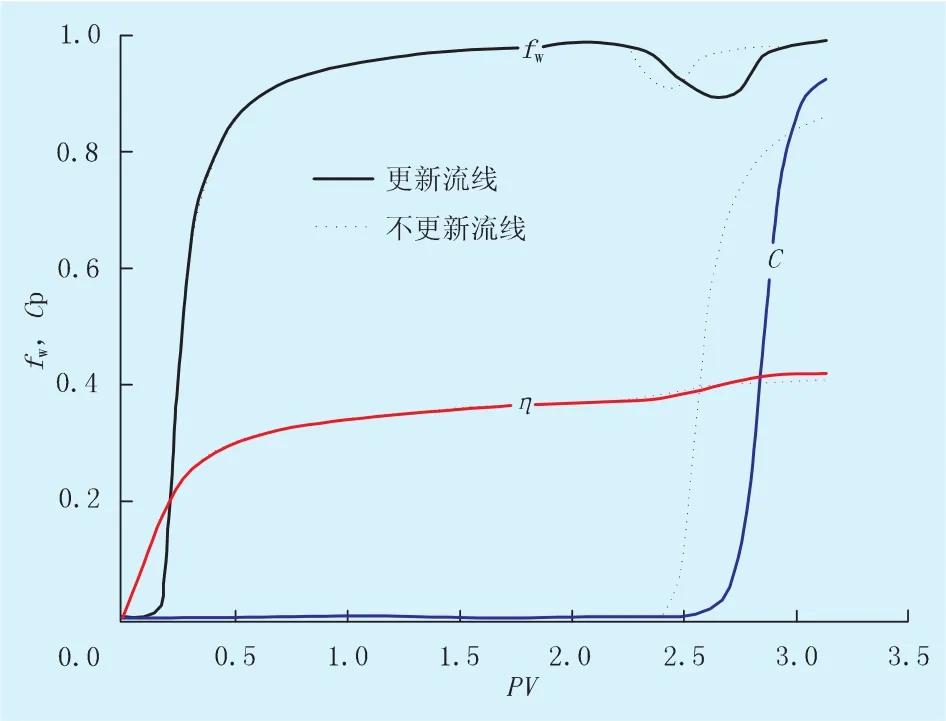
圖4 流線更新對聚合物驅流線模擬的影響

5 結論

(1)考慮聚合物驅過程中黏度變化及吸附效應，建立了聚合物驅流線模型。

(2)運用IMPES求解壓力方程，并運用Pollock方法追蹤流線;飽和度方程和聚合物濃度方程采用了高階精度顯式全變差遞減(TVD)差分方法求解，保證了差分方法的精確性。

(3)編寫了聚合物驅流線模擬程序，進行了流線更新;預測了五點井網聚合物驅過程，并與商業軟件進行了對比，驗證了流線更新方法的有效性。

［1］Need ham R B，Peter D H.Polymer flooding review［J］.SPE J，SPE17140，1987:1503 －1507.

［2］王啟民，冀寶發，隋軍，等.大慶油田三次采油技術的實踐與認識［J］.大慶石油地質與開發，2001，20(2):1－8.

［3］劉歆，周鳳軍，張迎春，等.海上油田稀井網大井距聚合物驅應用與分析［J］.特種油氣藏，2011，18(3):104－108.

［4］Patton J T，Coats K H，Colegrove G T.Prediction of polymer flood performance［J］.SPEJ，SPE2546，1971:72 －84.

［5］Thiele M B，Batychy R P，Pollitzer S，et al.Polymer－Flood Modeling using streamlines［C］.SPE115545，2010:313 －322.

［6］侯健，王玉斗，陳月明.聚合物驅數學模型的流線方法求解［J］.水動力學研究與進展，2002，17(3):343－352.

［7］侯健，李振泉，王玉斗，等.考慮擴散和吸附作用的聚合物驅替過程滲流數值模擬［J］.計算物理，2003，20(3):239－244.

［8］姚軍，吳明錄，胡航.堿聚合物復合驅油藏流線數值試井解釋模型及其應用［J］.石油學報，2008，29(6):894－902.

［9］Martin J C，Wegner R E.Numerical solution of multiphase two－dimensional incompressible flow using stream－tube relationships［C］.SPE7140，1979:313 －323.

［10］Pollock D W.Semi－analytical computation of path lines for finite － difference models［J］.Ground Water，1988，26(6):743–750.