開關電源環路補償計算及輔助軟件Mathcad的應用

王云 韓立峰（北京全路通信信號研究設計院有限公司，北京 100073）

隨著電子設備小型化、智能化，大量數字電路的引入，對開關電源系統的穩定性及可靠性提出了更高的要求，而環路補償對電源系統的穩定性、可靠性起著決定作用，在產品的開發過程中，通過簡單的試驗調試來確定環路補償參數，這種在實驗室里調試出來的參數不一定能夠滿足各種實際的使用情況。因此必須清楚電源系統環路的穩定性、相位裕量、增益裕量。有的放矢，通過明確的計算和仿真，設計出的產品才是科學的、合理的、可靠的。

本文介紹常用的補償電路以及借助輔助軟件計算了BUCK電路的環路補償參數。

1 環路補償介紹

1.1 環路穩定的條件

在自動控制理論中，根據乃奎斯特環路穩定性判據，如果負反饋系統在穿越頻率點的相移為180°，那么整個閉環系統是不穩定的。

Vout=[Vin-Vout×H（s）]×G（s）

Vout/Vin=G（s）/（1+G（s）×H（s））

準則1：在穿越頻率處，總開環系統要有大于30°的相位裕量。

準則2：為防止-2增益斜率電路的相位快速變化，系統的開環增益曲線在穿越頻率附近的增益斜率應為 -1（-20?dB/10 倍頻程）。

準則3：增益裕量是開環系統的模的度量，該變化可能導致曲線剛好通過-1點。一般需要6?dB的增益裕量。（應當注意，并不是絕對要求開環增益曲線在穿越頻率附近的增益斜率必須為-1，但是由于-1增益斜率對應的相位曲線相位延遲較小，且變化相對緩慢，因此它能夠保證當某些環節的相位變化被忽略時，相位曲線仍將具有足夠的相位裕量，使系統保持穩定。）

1.2 典型補償電路介紹

1）?單極點補償

K（s）=-Vout（s）/Vin（s）=R2/（R1（1+R2C2S））

2）單零點補償

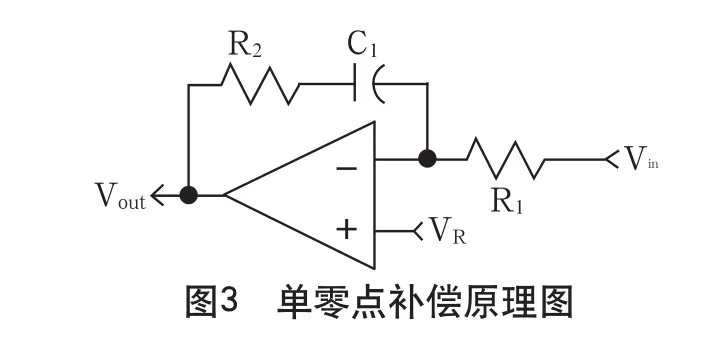
K（s）=-Vout（s）/Vin（s）=R2（1+R1C1S）/R1

3）單零單極補償

K（s）=-Vout（s）/Vin（s）=（1+R2C2S）/（R1C2S）

4）雙零單極補償

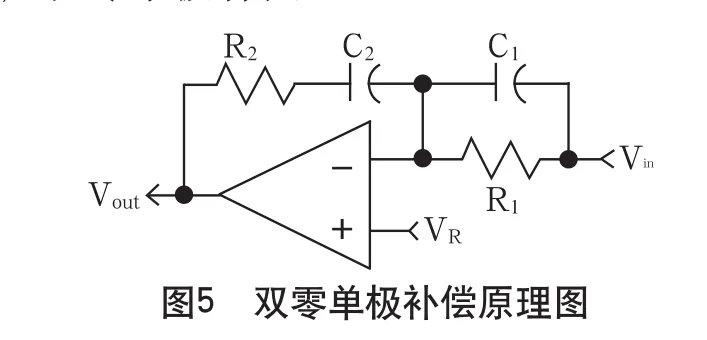
K（s）=-Vout（s）/Vin（s）=（1+R2C2S）（1+R1C1S）/（R1C2S）

2 補償參數計算

BUCK電路環路補償電路的選擇及環路補償的計算，如圖6所示。

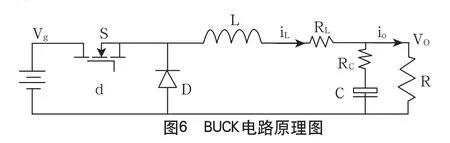
BUCK電路在CCM情況下控制（占空比D）到輸出（電壓Vo）的小信號傳遞函數：

Gvd（f）=Vg×（1+j×2πf/ωZC）/[1+j×2πf/（Q×ω）+（j×2πf）2/ω2]

00

設定，輸入Vg=20?V，占空比0.5，輸出10?V，負載電阻1??，其他設定如下：

ω=2πf；j=；s=jω；Vg=20；D=0.5；L=20μH；C=940μF ；RL=0.0001?? ；RC=0.037?5?? ；R=1??；ω0=1/；ωz1=RL/L；ωZC=1/（Rc×C）；ωZP=1/（R*C）；Q=1/{ω0×[L/R+（RL+RC）*C]}

Tvd（f）=20lg（|Gvd（f）|）

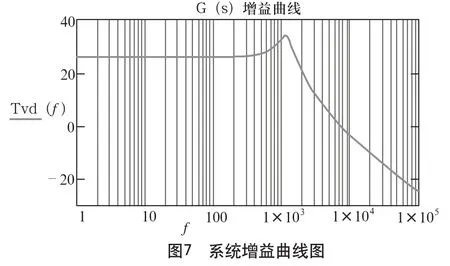
這是一個典型的低通濾波器，低頻時增益保持不變，在LC產生的雙極點處（頻率為1.16?kHz），增益曲線以-2的斜率衰減，在電解電容的ESR產生的零點處（頻率為4.5?kHz），增益曲線的斜率由-2變成-1。相位的變化情況如圖8所示。

θ（f）=arg（Gvd（f））/π×180

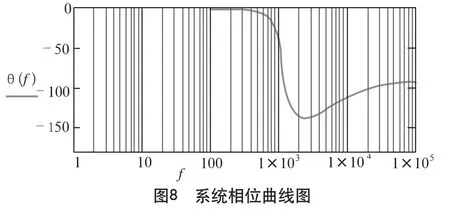
看起來還不錯，電容ESR引起的零點部分抵消了LC雙極點導致的相移，使得在穿越頻率點上還保持足夠的相位裕量：

root（Tvd（f）,f）=7.212×103Hz

θ（7?212?Hz）+180°=61.77°

從上面的計算中，可以獲得主電路傳遞函數G（s）的穿越頻率為7.2?kHz，相位裕度為61.77°。但是，靜態增益實在太低了，只有26?dB，為了消除靜態誤差，就必須提高靜態增益采用單零單極補償電路。

我們希望開環傳遞函數G（s）×H（s）的穿越頻率為10?kHz，而前面計算的G（s）的穿越頻率為7.2?kHz，那么H（S）將把整體的穿越頻率往后推延2.8?kHz。計算得出補償電路參數 R1=3?k?

R2=22.6?k?；C2=4.7?nF

H（f）=（1+j×2π×f ×R2×C2）/（5×j×2π×f×R2×C2）

Tv（f）=Gv（f）×H（f）

計算完成之后，來看補償的效果。

穿越頻率fc=10.08?kHz；相位裕度為60.6°。結果是相當完美的，完全達到了設計要求。

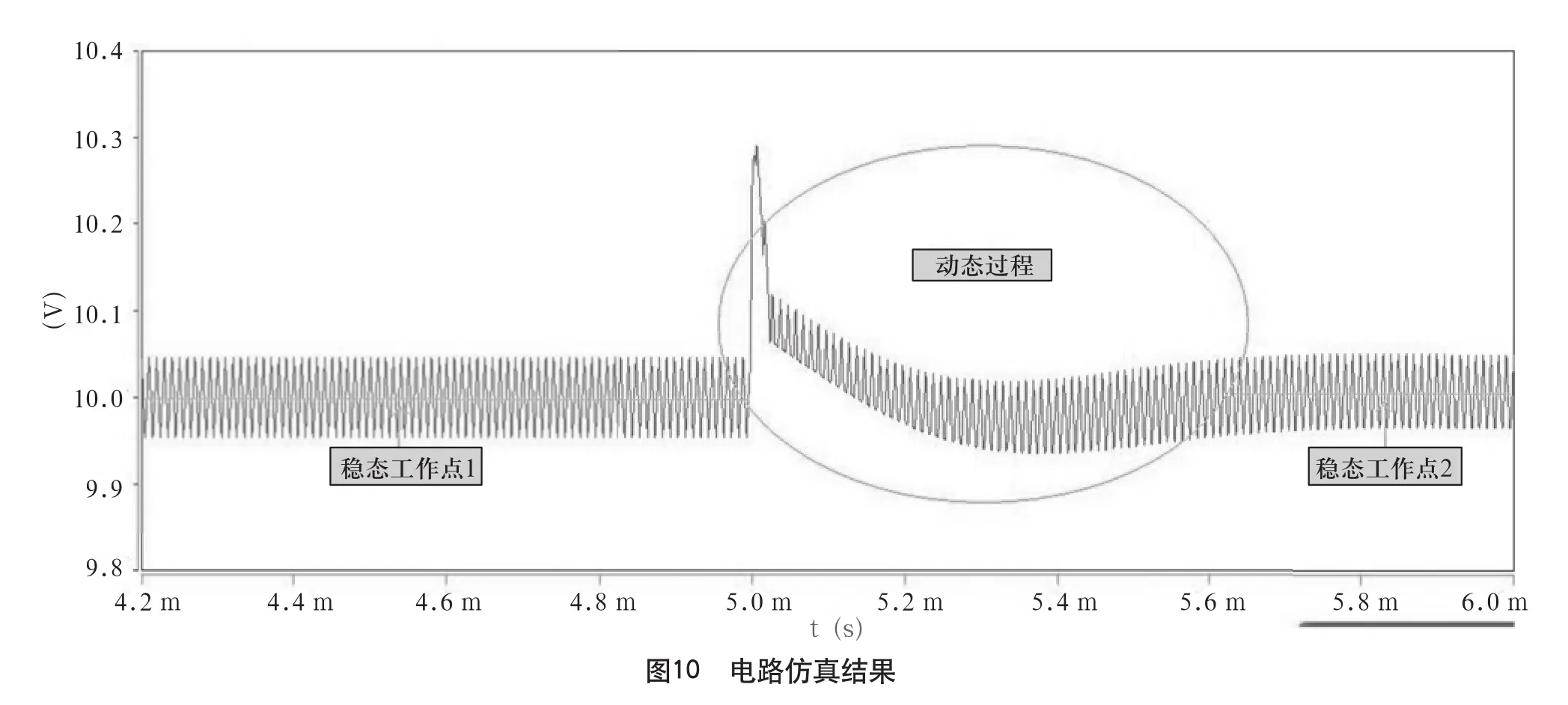
3 仿真驗證

從圖10看出輸出電壓從一個穩態工作點1到達穩態工作點2，需要大約0.6?ms的時間，輸出過沖幅度為0.3?V，其后快速回落，經輕微震蕩后達到穩態工作點2。從仿真可以看出，動態響應速度很快，過沖小，振蕩少，完全能夠滿足要求。

[1]鄭桂水.Mathcad2000實用教程{M}.北京：國防工業出版社，2000.

[2] 普利斯曼，比利斯，莫瑞.開關電源設計[M].王志強，肖文勛，虞龍，譯.北京：電子工業出版社，2010.

[3]潘豐，張開如.自動控制原理[M].北京：北京大學出版社，2006.