基于相似度原理的船舶電力推進系統仿真可信度研究

劉建波

?

基于相似度原理的船舶電力推進系統仿真可信度研究

劉建波

（海軍駐上海江南造船集團有限責任公司軍事代表室，上海 201913）

為了更好地檢驗船舶電力推進系統仿真的可信度，結合相似度原理和模糊綜合評判方法，對船舶電力推進系統的定性與定量指標進行綜合分析。將影響系統仿真的可信性因素綜合起來建立評價指標體系，并依據層次分析法原理確定各指標的權重向量。針對專家所給的權重判斷矩陣，進行次序一致性檢驗和基本一致性檢驗。確定子系統隸屬函數。驗證仿真系統可信性分析方法的可行性，并取得了較好的結果。

船舶電力推進系統 模糊綜合評判 相似度 可信性分析

1 評價指標體系的建立

隨著仿真技術的不斷發展和船舶電力推進系統的廣泛應用，必需對船舶電力推進系統仿真進行可信性分析。研究船舶電力推進系統仿真可信性時，首先需要確定系統仿真的評價指標體系。

船舶電力推進的系統仿真在建立時，首先需要確定系統的概念模型，然后通過計算機語言建立系統的計算機模型，確定計算機模型時需要系統的相關參數。最后通過系統的仿真結果進行分析。依據指標評價體系的建立原則，選擇如下指標分析船舶電力推進系統仿真的可信性。本文只給出三層評價指標體系。

1) 系統仿真模型；

2) 系統仿真結果；

3) 數據有效性。

根據以上分析，建立船舶電力推進系統仿真可信性分析的評價指標體系。具體如圖1所示。

2 可信性分析評價方法

船舶電力推進系統仿真可信性分析的評價指標體系中，有的指標類型為定量的，有的則為定性的，不能采用單一的評價方法進行分析。模糊綜合評判是通過專家打分對系統進行分析，相似度原理是依據各指標的仿真數據與實際數據或期望數據分析其相似度。鑒于船舶電力推進系統仿真可信性分析評價指標體系為分層次的，在評判過程中需要考慮各指標在綜合評價過程中的權重大小。因此，根據模糊綜合評判和相似度原理的特點，結合層次分析法原理，對船舶電力推進系統的仿真可信性進行綜合分析。

圖1 船舶電力推進系統仿真可信性分析評價體系

整個船舶電力推進系統的仿真可信性分析過程如下：

1) 依據系統相關標準及評價指標體系建立原則，建立評價指標體系。

2) 利用層次分析法原理，確定各指標在綜合評判過程中的權重大小。

3) 結合模糊綜合評判原理和相似度原理法，對船舶電力推進系統仿真進行可信性分析。

2.1 層次分析法原理

分析船舶電力推進系統的仿真可信性時，需要確定各指標在評判過程中所占的權重大小[1]。

1) 利用層次分析法原理求取指標權重時，首先需要專家給出各指標相對于上層指標的相對重要性，也即判斷矩陣。專家給出指標的判斷矩陣依據互反性1-9標度表。具體如表1所示。

表1 互反性1-9標度表

2) 給出判斷矩陣，然后對指標進行權重排序和一致性檢驗。權重排序采用特征值法求取。

具體求解步驟為：

①根據標度原理，構造兩兩比較矩陣

②將判斷矩陣A的各列作歸一化處理，即

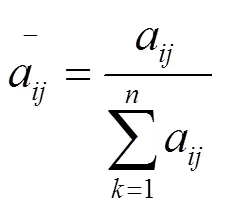
③求出判斷矩陣A每一行各元素之和，即：

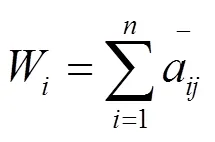
④對W進行歸一化處理，即：

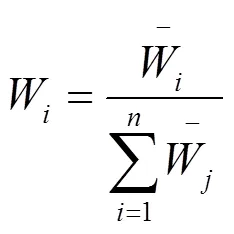
⑤進行一致性檢驗

一致性檢驗是針對判斷矩陣是人們主觀判斷而得，不可避免有估計誤差而進行的。對判斷矩陣進行一致性檢驗分為次序一致性檢驗和基本一致性檢驗。次序一致性是檢驗判斷矩陣內元素，a>1，a>1能否導出a>1，若能則滿足次序一致k性，否則不滿足。基本一致性是檢驗一致性比例CR是否小于0.1，若小于則滿足基本一致性要求，否則不滿足。

判斷矩陣的次序一致性和基本滿意一致性之間沒有必然的聯系：具有次序一致性的判斷矩陣不一定具有基本滿意一致性；而具有基本滿意一致性的判斷矩陣又不一定具有次序一致性。其中次序一致性是判斷矩陣可用的基本條件，違反次序一致性的判斷反映了決策者對問題缺乏起碼的深思熟慮，而由不具備次序一致性的判斷矩陣導出的權值不可能是對某種屬性合理的測度。因此，對決策者給出的判斷矩陣，首先應該檢查其是否具有次序一致性，然后再檢查其是否具有基本滿意一致性[2]。

次序一致性的檢驗采用文獻[3]中的檢驗步驟。基本一致性的步驟如下：

①根據權重排序方法計算判斷矩陣的最大特征值λ。

②計算一致性指標CI

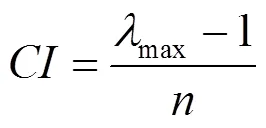
表2 1~7階矩陣的RI值

2.2 模糊綜合評判

船舶電力推進系統仿真可信性評價指標體系中，有的指標類型為定性的，如評價體系中子指標：系統仿真模型、數據有效性，不能采用定量的方法進行分析。因此，需要根據專家知識，利用模糊綜合評判法對系統進行定性分析[4-7]。模糊綜合評判的基本步驟為：

1）針對影響船舶電力推進系統仿真可信性的指標因素，建立因素集：

2）根據所確定的因素集，建立相應的評價標準，即評判集：

4）模糊綜合評判：

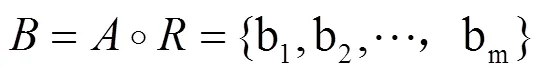
2.3 相似度原理

相似度[8]是為衡量系統間相似程度的大小所進行的量化，適用于定量指標的判斷分析。

各個子系統的相似元計算公式為：

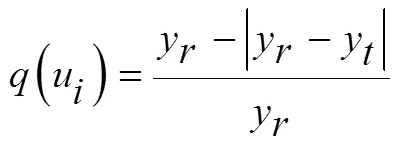
2.3.1數據預處理

對于船舶電力推進系統仿真進行可信性分析時，評價體系中的子指標系統仿真結果，其仿真數據與實際系統數據均可得到，故可采用相似度原理分析。

對于系統仿真所得的結果，指標類型不同，其所得數據類型也不同。有的指標數據越小其相似度越高，有的則是數據越大相似度越高。因此，對系統仿真結果進行可信性分析時，首先需要通過線性變換方法對原始數據進行歸一化處理。

①當指標值越大時系統仿真結果越好，即指標類型為效益型。數據預處理公式：

Y=(X-min)/(max-min) (10)

②當指標值越小時系統仿真結果越好，即指標類型為成本型，數據預處理公式：

Y=(max-X)/(max-min) (11)

式中：X為系統仿真結果所得的值，Max(或Min)為對同一指標而言船舶電力推進系統可能出現或期望的最大值(或最小值)。

2.3.2相似度隸屬函數的求取

對船舶電力推進系統仿真進行可信性分析時，評價方法中既包含有定性方法也包含有定量方法。本文通過采用自適應神經網絡模糊推理系統ANFIS來建立模糊模型，將系統所得的相似度轉化為與模糊綜合評判一致的模糊向量[9]。

自適應神經網絡模糊推理系統是通過訓練樣本來訓練網絡，并獲取系統初始隸屬函數，最終利用反向傳播算法來修正初始隸屬函數，求取最終系統的隸屬函數。而通常系統隸屬函數的確定是通過專家直接給出或者依據經驗數據而得，所得到的隸屬函數并非能完全反應真實系統，隸屬函數中各節點的數據如果選取不恰當，會對系統的模糊判斷帶來誤導[10]。

較之于憑主觀經驗設定的系統隸屬函數，自適應神經網絡模糊推理系統能夠更好的反映系統特點，并能依據系統特點反向傳播對隸屬函數進行修正，直到誤差達到一定范圍終止。

對于子指標B系統仿真結果而言，可以依據系統在工況C3、C4、C5、C6的仿真數據與實際數據求取各工況與實際相比的相似度，并依據不同工況相對于系統仿真結果的權重大小求取子指標B的相似度。通過數次仿真獲取不同子系統的相似度，并選取數組訓練樣本和測試樣本。設定C3、C4、C5、C6指標的相似度為輸入集，B指標的相似度為輸出集，并利用反向傳播算法來修正并確定隸屬函數。

3 實際算例

3.1 系統各指標權重的確定

對于船舶電力推進系統仿真可信性分析評價體系中各指標權重的計算，采用層次分析法原理，通過專家打分獲取判斷矩陣，然后利用特征根法計算權重向量并進行次序一致性和基本一致性檢驗。若不滿足要求，要求專家對判斷矩陣進行重新修正，直到滿足一致性要求為止。鑒于篇幅原因，本文只給出權重結果。其中WA為B1、B2、B3相對于A的權重向量。WB1、WB2、WB3為指標B1、B2、B3下層指標相對于上層指標的權重。

WA= {0.4286, 0.1429, 0.4286}.

WB1= {0.5, 0.5}.

WB2= {0.25, 0.25, 0.25, 0.25}.

WB3= {0.0579, 0.2002, 0.3710, 0.3710}.

3.2 模糊綜合評判

針對指標B1和B3的類型均為定性指標，采用專家打分的方式進行評判分析。通常，人們對指標的評價常用滿意程度來表示，因此，劃分評判集時可以通過滿意程度來劃分。但評判集劃分并非越多越好，越多則需要更多的模糊控制規則。為此，對于指標B1和B3而言，將其評判劃分為4級，分別為{好、較好、較差、差}，即V={好、較好、較差、差}。專家在打分時相應的判斷依據如表3：

表3 專家判斷依據

設U={U1、U2、U3}，U1、U2、U3分別表示系統仿真模型、系統仿真結果、數據有效性三個指標。則相應的子指標可以表示為:U1={U11、U12}，U2={U21、U22、U23、U24}，U3={U31、U32、U33、U34}。通過專家對指標U1、U3的評判及統計分析，得到如下模糊判斷矩陣。

3.3 系統相似度

根據系統仿真在啟航、倒車、停車及突變負載工況下的數據以及實際系統在對應工況下的相應數據，求取各指標的相似度。

對于指標B2而言，系統仿真數據與實際系統數據可以通過實驗或測量而得。對于船舶電力推進系統而言，隨機選取一組仿真系統在不同工況下的數據，并與相同工況下的實際數據進行比較。其中數據見表4。

利用式（9）、(10)、(11)求取C3、C4、C5、C6的相似度：

利用層次分析法所得C3、C4、C5、C6相對于B2的權重向量，根據式(7)、(8)求取指標B2的相似度，得：

=0.25*0.8+0.25*0.87+0.25*0.83+0.25*0.76

=0.815

表4 仿真數據與實際系統相應數據

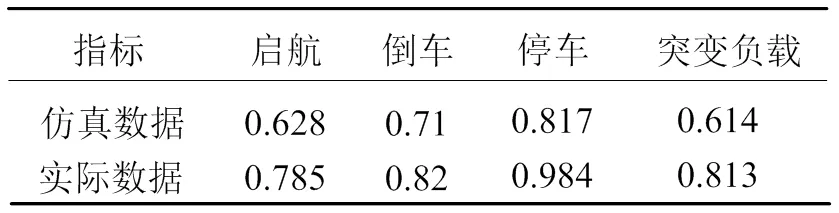
為了將仿真所得結果模糊化，確定仿真結果的隸屬函數，通過對系統進行多次仿真并隨機選取20組數據作為訓練樣本，5組數據作為測試樣本，網絡訓練200次，隸屬函數類型設為高斯型，隸屬度個數與模糊綜合評判劃分個數相同，為4個。并利用反向傳播算法來修正初始隸屬函數。最終所得的初始隸屬函數和訓練后的隸屬函數如圖2。訓練過程中樣本集和測試集的均方根誤差變化情況如圖3。由圖3中兩條誤差曲線的變化情況可知，模糊系統的設計與數據是匹配的，滿足要求。

通過查詢訓練后所得的模糊隸屬函數曲線，如圖2所示，將上述求得的相似度轉化為模糊向量，得：

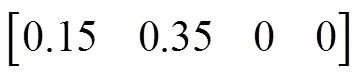
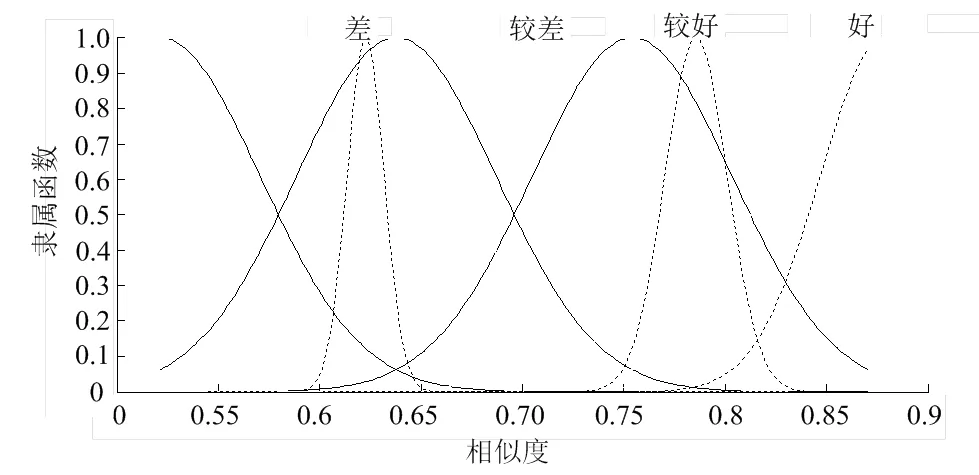
圖2 初始和訓練后的隸屬函數

圖3 訓練過程中均方根誤差的變化曲線

3.4 系統仿真可信度計算

針對B1、B2、B3模型，利用模糊評判原理進行二級模糊綜合評判。得到B1、B3的一級模糊評判矩陣為:

B1= WB1*R1

= [0.45 0.3 0.15 0.1]

同理得B3一級模糊評判矩陣為：

B3= [0.3088 0.3113 0.2629 0.1171]

以 B1、B2、B3為元素，構造單因素模糊向量，進行二次模糊評判，得：

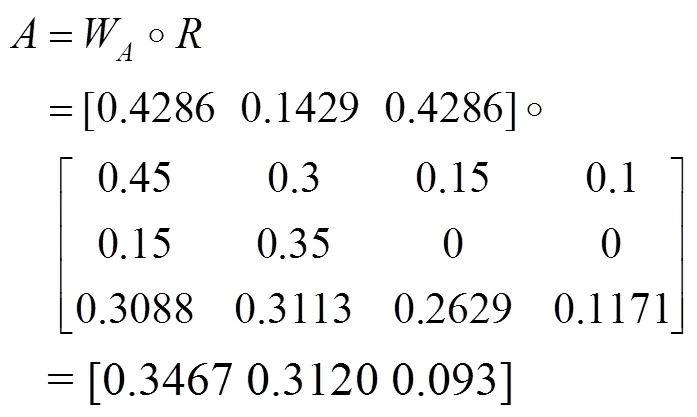
由上述計算結果可知其最大隸屬度為0.3467。根據最大隸屬度原則，最大隸屬度對應于模糊評語的“好”。因此可以得到該船舶電力推進系統仿真的可信性為“好”。

4 結論

本文通過結合相似度原理和模糊綜合評判兩種定性與定量的方法，對船舶電力推進系統仿真進行可信性分析。首先建立船舶電力推進系統仿真可信性分析評價指標體系，并利用層次分析法原理確定各指標的權重大小；然后針對各指標特點采用相應的方法進行分析計算，利用自適應神經網絡模糊控制系統對定量方法所得結果進行模糊化；通過模糊綜合評判確定系統最終的可信度。

該方法能夠更好地解決船舶電力推進系統中不同指標類型的特點，可以較為客觀、綜合、全面的分析船舶電力推進系統的仿真可信度。同時該方法對定量方法所得結果進行模糊化時，有效地避免了通過專家經驗或歷史數據確定隸屬函數所帶來的不確定性，真實的反應了系統特點。該方法理論清晰，便于操作，且工作量不大，可以較好的應用于實際系統。

[1] 徐樹柏. 層次分析法[M]. 天津大學出版社,1988.

[2] 朱建軍. 層次分析法的若干問題研究及應用[D]. 東北大學博士論文, 2005.

[3] 朱建軍, 王夢光, 劉士新. AHP判斷矩陣一致性改進的若干問題研究[J]. 系統工程理論與實踐. 2007. 1:18-22.

[4] 楊軍. 基于模糊理論的衛星導航系統綜合效能評估研究[J]. 宇航學報. 2004, 25(2): 147-151.

[5] 岳韶華, 周國安, 王穎龍. 地面防空作戰效能的模糊綜合評價[J]. 系統工程與電子技術. 2001. 3(9): 67-69.

[6] 肖峻, 王成山, 周敏. 基于區間層次分析法的城市電網規劃綜合評判決策[J]. 中國電機工程學報. 2004, 24(4): 50-57.

[7] 朱宗林, 郭世民. 自動控制裝置系統綜合評估研究[J]. 自動化學報, 1999, 25(2): 199-203.

[8] 徐迪. 基于相似理論的系統仿真可信性分析[J]. 系統工程理論與實踐, 2001(4): 49-52.

[9] 吳曉莉, 林哲輝等. MATLAB輔助模糊系統設計[M]. 西安電子科技大學出版社, 2002.

[10] 王石青, 邱林, 王志良等. 確定隸屬函數的統計分析法[J]. 華北水利水電學院學報, 2002. 23(1): 68-71.

Research on the Credibility of the Ship Electric Propulsion Simulation System Based on the Comprehensive Evaluation

Liu Jianbo

(Naval Representatives Office in Jiangnan Delta Refco Group Ltd, Shanghai 201913, China)

U664.14

A

1003-4862（2013）04-0008-05

2012-11-15

劉建波（1970－），男。專業方向：艦船電力推進。