能量代謝守恒法無創血糖檢測算法研究*

朱健銘，陳真誠

(1.中南大學地球科學與信息物理學院，長沙410083;2.桂林電子科技大學生命與環境科學學院，廣西桂林541004)

糖尿病是一種常見的代謝性疾病，以慢性高血糖為主要特征，并能引發糖類、脂肪、蛋白質、電解質和水等的代謝紊亂，嚴重危害人類健康。目前此病尚無根治方法，早期診斷，早期預防是首選措施。對于糖尿病人而言，需要經常檢測自己的血糖值以指導用藥，對于健康人而言，也需要定期檢查空腹血糖值及餐后2 h血糖值以盡早發現是否出現空腹血糖損害或葡萄糖耐量損害。

目前血糖檢測主要采用血液生化檢測和微創檢測方法［1－9］，前者需要在醫院進行，采集患者血液，后者也需要刺破手指采集血液，給患者帶來極大痛苦和心理負擔，同時創口易感染。本文提出的能量代謝守恒法［10－13］無創血糖檢測方法無需采集血液，是一種無創傷，無痛苦，無感染的方法。臨床實驗表明，與生化分析儀(AMS－AUTOLAB18)對比，此方法用以檢測糖尿病患者血糖濃度的準確度達到86%。

1 檢測原理

在日本學者Cho ok kyung等人提出的代謝熱整合法［14］的基礎上，桂林電子科技大學陳真誠等人完善并優化了該理論，提出能量代謝守恒法，設計并制作了無創血糖檢測傳感器，只需通過患者手指無創地采集一些生理參數，即能計算出血糖值。能量代謝守恒法的基本思想是在人體手指指端，血液中的葡萄糖氧化產生能量、二氧化碳和水，此能量大部分通過手指局部的熱傳導，熱輻射，熱對流和熱蒸發等途徑散失。通過合適的裝置和傳感器檢測這部分的能量散失以及血液中的氧氣水平就能計算出血液中葡萄糖的量，即血糖值。由此建立的血糖檢測數學模型如下

式(1)中GLU為血糖值，M為與熱交換相關的代謝率，SPO2為血氧飽和度，BF為血流量，PF為脈率，c為常數。F1為某種函數關系，即無創血糖檢測算法。

2 傳感器設計

根據能量代謝守恒法的基本理論和上述數學模型，設計出無創血糖檢測探頭如圖1所示。

圖1 無創血糖檢測探頭設計圖

圖1中1是環境濕度傳感器，2是環境溫度傳感器，3是金屬片遠端溫度傳感器，4是金屬片，5是金屬片近端溫度傳感器，6是手指附近濕度傳感器，7是手指表面溫度傳感器，8是光電二極管，9是雙波長發光二極管，10是電源接口，11是數據輸出口，12是熱電堆紅外輻射傳感器。在傳感器的選型上，溫度傳感器采用LM35CAH集成溫度傳感器，濕度傳感器采用HIH4000－3集成濕度傳感器，熱電堆紅外輻射傳感器的型號為A2TPMI334－L5.5 OAA060，金屬片選用鎂片。檢測時，食指尖部放入8和9之間的空腔內，第2指節和第3指節貼在6和7上部的平面上。

3 檢測算法與結果分析

檢測原理中給出的式(1)未將各參數細化成方便檢測的參數，因此在檢測前需根據無創血糖檢測探頭的設計，將參數細化，再選擇合適的檢測算法。

3.1 檢測參數細化

式(1)中的M，即與熱交換相關的代謝率，應包括手指指端與環境的傳導散熱、對流散熱、輻射散熱、以及蒸發散熱。在手指附近空氣流動較緩慢的情況下，對流散熱量和傳導散熱量可以認為是手指表面溫度和環境溫度之差的函數，蒸發散熱量是手指附近濕度和環境濕度之差的函數，輻射散熱量是手指輻射溫度和背景輻射溫度之差的函數。因此可以得到M的計算公式為

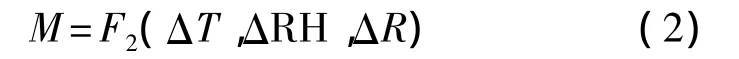
式(2)中，ΔT為手指表面溫度和環境溫度之差，ΔRH為手指附近濕度和環境濕度之差，ΔR為手指輻射溫度和背景輻射溫度之差。F2為某種函數關系，即熱交換代謝率算法。

式(1)中的SPO2可以采用手指指端雙波長光電容積脈搏波計算得出，PF可以采用手指指端紅外光電容積脈搏波分析得出，此部分理論較為成熟，不再贅述。BF可以采用熱清除法的相關理論，通過金屬片的近端溫度和遠端溫度的變化情況計算得出。將式(2)代入式(1)，可以得到血糖值的計算公式如下

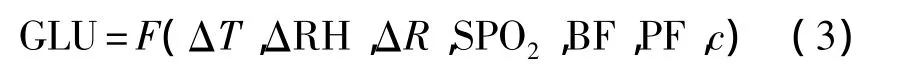
式(3)中，F為某種函數關系，即無創血糖檢測算法，其余參數和式(1)、式(2)中的意義相同。

3.2 檢測算法

由于與熱交換相關的代謝率計算起來相當復雜，但根據式(3)給出的函數關系，可以采用多元統計分析的方法求解血糖值GLU。

3.2.1 多元線性回歸

多元統計分析中應用最廣的是多元線性回歸理論，當一個現象與多個因素相聯系時，往往可以由多個自變量的某種線性組合來估計因變量。

根據多元線性回歸的理論，可以建立如下血糖檢測的數學模型

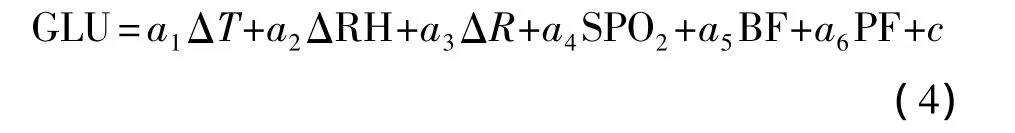
其中a1～a6為常數，即回歸系數，其余參數和式(3)中的意義相同。此模型細化了測量參數，將代謝率細化為一些方便傳感器檢測的量，同時也忽略了一些對血糖檢測貢獻小的參數［10－12］。

為了求解回歸系數，在實驗室環境下，環境溫度25℃，相對濕度71%，采集了29組數據，其中9組數據來自健康被試，20組數據來自糖尿病患者。首先將這些數據導入SPSS 19.0，在簡單的預處理之后，對這些數據進行多元線性回歸分析，可以得到以下回歸數據，如圖2和表1所示。

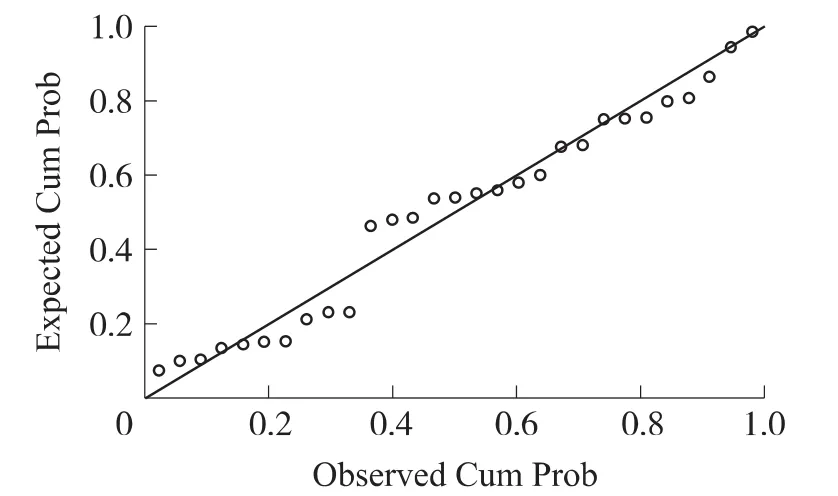
圖2 回歸標準殘差正態分布P－P圖

圖2的橫坐標是觀測變量的累積比例，縱坐標是指定分布的累積比例，可以看出圖中的29個點近似為一條直線，這說明檢驗數據近似符合指定分布。

表1 多元線性回歸參數

表1是回歸分析的統計量，可以看到相關系數R為0.845，標準差為3.304 18。這說明采用多元線性回歸來求解血糖值是可行的，但是此模型的相關系數R還不夠理想，標準差稍大。

3.2.2 主分量分析

主分量分析又稱主成分分析，是一種常用的多元統計分析方法，它是通過某種線性組合使某個或某些變量的解釋方差增大，具有較大解釋方差的變量就是主分量。觀察式(4)可以發現，SPO2，BF，PF這三個變量均與血液中的氧含量相關，可以將這三個變量融合成一個變量作為求解血糖值模型的參數，根據血液動力學和生理學的知識可以得知，這三個變量均與氧含量成正相關。假設氧含量

其中O2為氧含量，p為歸一化參數，可由實驗測得，其余參數和式(3)中的意義相同。考慮式(3)和式(5)，可以得到一個簡化的血糖檢測模型

其中，Q為某種函數關系，即無創血糖檢測算法，其余參數和式(3)、式(5)中的意義相同。

在式(6)所示的血糖檢測模型中，究竟哪些變量對血糖值的貢獻率大呢?可以采用主分量分析法求解。將上述29組數據導入SPSS 19.0，簡單預處理之后，采用因子分析中的主成分分析功能處理數據，可以得出如下分析結果，如表2和表3所示。

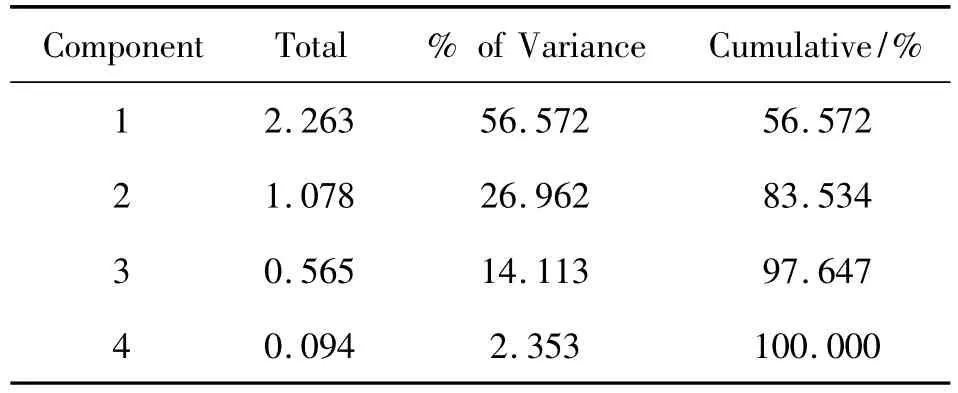
表2 分量特征值和方差貢獻率

如表2所示，分量1和2的特征值均大于1，它們的方差貢獻率分別為56.572%和26.962%，累積方差貢獻率為83.534%，這說明可以選取分量1和2作為該模型的主分量，而分量3和4對血糖值的貢獻較小。

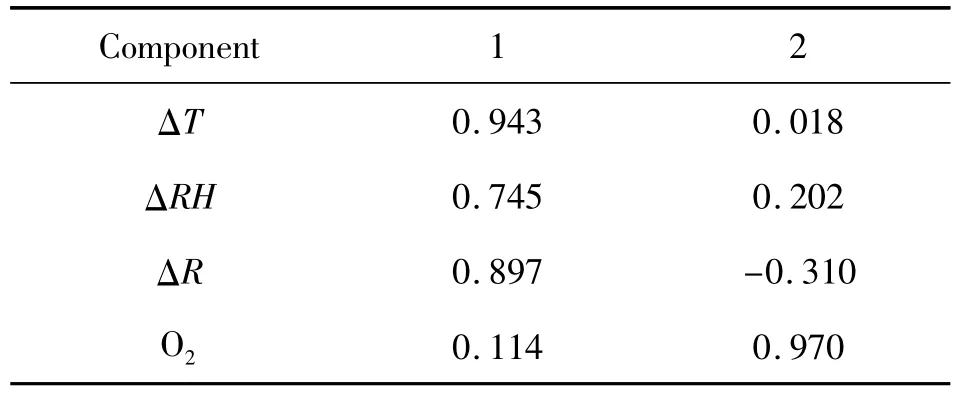
表3 分量矩陣

表3給出了分量1和2的組成成分，可以看到分量1主要由ΔT，ΔRH，ΔR三者構成，分量2主要由O2構成。此分析結果和能量代謝守恒法無創血糖檢測的基本原理是吻合的，葡萄糖在體內有氧氧化過程如下

分量1主要體現方程式(7)右邊ATP的量，而分量2主要體現左邊氧氣的量。

可以對分量1和分量2使用SPSS 19.0做多元線性回歸分析，可以得出如下分析結果，如圖3和表4所示。

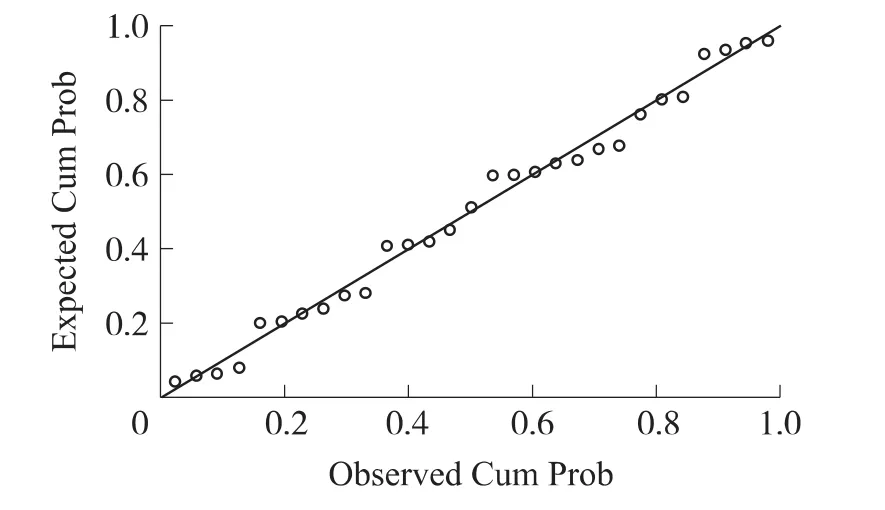
圖3 回歸標準殘差正態分布P－P圖

圖3的橫坐標是觀測變量的累積比例，縱坐標是指定分布的累積比例，可以看出圖中的29個點近似為一條直線，這說明檢驗數據近似符合指定分布。同時，對比圖2可以看出，圖3中散點的線性度比圖2要高。

表4 多元線性回歸參數

表4是回歸分析的統計量，可以看到相關系數R為0.764，標準差為3.835 73。對比表1可以發現，采用分量1和2做回歸分析的結果較差，原因是分量1和2的累積方差貢獻率只有83.534%，但是回歸變量的個數大大減少了。因此，主分量分析方法提供了一種降維的手段，便于應用其他的多元統計分析方法，如聚類分析，判別分析等。在檢測誤差可以接受的情況下，可以用分量1和2計算血糖值。

3.3 檢測結果與分析

為了驗證檢測模型的準確性，在實驗室環境下，環境溫度25℃，相對濕度73%，采集了30組數據，全部來自糖尿病患者，檢測時間固定在中午進食后2 h。檢測前，被試未進行劇烈運動，心情較為平靜，手指指面保持清潔，檢測結果如圖4所示。

圖4 無創血糖檢測實驗結果

如圖4所示，橫坐標是血糖檢測值，采用多元線性回歸模型計算，計算方法如式(4)所示。縱坐標為血糖真實值，采用生化分析儀(AMS－AUTOLAB18)檢測得出。可以看出兩種檢測方法的相關性較好，經計算，其相關系數R=0.86。實驗結果的相關系數比回歸模型的相關系數略大，可能是因為實驗對象均為糖尿病患者，其餐后2 h血糖值大部分都在10 mmol/L以上。檢測結果的誤差可能與以下因素有關:①無創血糖檢測模型的準確性，此模型忽略了用于生化反應的部分能量損失;②多元線性回歸模型的準確性，由于用于標定的數據較少，使得此模型的參數估計有誤差;③系統誤差，這是無創血糖檢測探頭數據采集引入的誤差;④檢測過程和環境，被試在檢測時必須保持靜息狀態，劇烈運動、心情焦慮、手指抖動等都會給檢測結果帶來誤差。

4 結論

本文根據能量代謝守恒法無創血糖檢測的基本理論，設計了無創血糖檢測探頭，采用多元統計分析的方法對實驗數據進行處理，導出了基于多元線性回歸的血糖值計算方法，實驗結果表明，此方法的擬合效果較好，相關系數R=0.845。用30組糖尿病患者的實驗數據驗證了多元線性回歸方法的有效性，檢測結果的相關系數R=0.86。采用主分量分析方法處理了檢測數據，找出了對血糖檢測影響最大的2個分量，在后續的研究工作中，可以結合主分量分析、因子分析、聚類分析和判別分析等多元統計分析方法處理數據，進一步提高檢測準確率。

［1］ Harutyun M，Emma D，Seungwan K，et al.Non-Invasive in vitro Sensing of D-Glucose in Pig Blood［J］.Medical Engineering and Physics，2012，34(3):299－304.

［2］ Seungwan K，Harutyun M，Jongchel K，et al.Noninvasive in vitro Measurement of Pig-Blood D-Glucose by Using a Microwave Cavity Sensor［J］.Diabetes Research and Clinical Practice，2012，96(3):379－384.

［3］ Christopher M，David H，Patricia C.Towards Blood Free Measurement of Glucose and Potassium in Humans Using Reverse Iontophoresis［J］.Sensors and Actuators B:Chemical，2012，166－167(5):593－600.

［4］ Cai Y Y，Cao D，He X H，et al.Continuous Glucose Monitoring System Based on Smart Phone［J］.Procedia Engineering，2012，29:3894－3898.

［5］ Sandeep K V.Non-Invasive Glucose Monitoring Technology in Diabetes Management:A Review［J］.Analytica Chimica Acta，2012，750(10):16－27.

［6］ Hisako H，Mihara M，Lida T，et al.Blood Glucose Measurement for Flap Monitoring to Salvage Flaps from Venous Thrombosis［J］.Journal of Plastic，Reconstructive and Aesthetic Surgery，2012，65(5):616－619.

［7］ Dongmin G，David Z，Lei Z，et al.Non-Invasive Blood Glucose Monitoring for Diabetics by Means of Breath Signal Analysis［J］.Sensors and Actuators B:Chemical，2012，173:106－113.

［8］ Enric M M.Non-Invasive Estimate of Blood Glucose and Blood Pressure from a Photoplethysmograph by Means ofMachine Learning Techniques［J］.Artificial Intelligence in Medicine，2011，53(2):127－138.

［9］ Miguel P，Hermann L T，Werner M． Infrared Spectroscopic Analysis of Human Interstitial Fluid in vitro and in vivo Using FT-IＲ Spectroscopy and Pulsed Quantum Cascade Lasers ( QCL ) :Establishing a New Approach to Non-Invasive Glucose Measurement［J］． Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy，2012，85( 1) : 61－65．

［10］朱健銘，陳真誠，金星亮，等.基于DSP技術的便攜式無創血糖檢測儀［J］.電子測量與儀器學報，2009，23(6):108－112.

［11］周茗思，陳真誠，朱健銘.便攜式無創血糖檢測儀的研制［J］.傳感技術學報，2011，24(7):946－949.

［12］陳真誠，金星亮，徐效文，等.一種無創血糖檢測儀的初步研究［J］.傳感技術學報，2008，21(7):1119－1123.

［13］ Chen Z C，Jin X L，Zhu J M，et al.Non-Invasive Glucose Measuring Apparatus Based on Conservation of Energy Method［J］.J Cent South Univ Technol，2009，16:982－986.

［14］ Cho O K，Kin Y，Hiroshi M，et al.Non-Invasive Measurement of Glucose by Metabolic Heat Conformation Method［J］.Clinical Chemistry，2004，50(10):1894－1898.