基于ANSYS有限元法的接觸系統電動力分析

黃蔚偈，蘭太壽，劉向軍

(福州大學電氣工程與自動化學院，福建 福州 350108)

上的磁感應強度相關，而作用在觸頭上的磁感應強度主要由觸頭的收縮

基于ANSYS有限元法的接觸系統電動力分析

黃蔚偈，蘭太壽，劉向軍

(福州大學電氣工程與自動化學院，福建 福州 350108)

繼電器接觸系統電動力主要由觸頭的HOLM力和導體的洛倫茲力組成。在沖擊電流試驗中，觸頭是否因電動力作用而斥開是考核電能表用磁保持繼電器安全性和穩定性的重要標準。首先通過有限元法結構分析，計算動靜觸頭的接觸半徑，再通過耦合場分析計算接觸系統各部件的電流密度分布和磁場分布，進而求解出電動力。對不同觸頭壓力和不同短路電流下的電動斥力進行了計算與分析，并研究了接觸系統各部件對電動力的影響，為接觸系統的改進提供基礎。

磁保持繼電器;電動力;接觸半徑;有限元分析

1 引言

當電流流過電器觸頭時，由于觸頭實際接觸面積很小，在接觸區域附近會發生電流線收縮，產生電動斥力，即Holm力。而通有電流的導電臂在周圍空間磁場的作用下，也會產生洛倫茲力，這兩種力的合力構成了接觸系統的電動斥力。在額定電流作用下該電動斥力比較小，對電器穩定性影響不大。但當觸頭系統承受沖擊電流時，導電臂和接觸表面的電流線密度急劇增加，空間磁場也成倍增長，此時感應出的電動力有可能使閉合的接觸系統斥開，產生嚴重的后果。標準要求電能表用磁保持繼電器的抗沖擊電流能力為額定電流的30倍，比一般磁保持繼電器的5～10倍要高得多。當進行沖擊電流試驗時，觸頭可能發生斥開現象，因此，電動斥力的研究對電能表用磁保持繼電器的安全性和穩定性有重要的意義。

電動斥力與接觸系統可動部件的電流密度和磁感應強度有關，因此，求解出各部分的電流密度和由電流產生的磁感應強度是準確求解電動力的關鍵。不同的電器接觸系統型式多樣且復雜，電流密度和磁感應強度用解析法較難求出，因此用傳統的電動力計算公式有一定的誤差，不能準確考慮到接觸系統電流密度的分布對電動力的影響。

隨著有限元計算軟件的發展，通過電流傳導分析和耦合場分析可以精確計算出接觸系統的電流密度分布和相應磁感應強度的分布，通過一定的后處理，便可方便計算出電動斥力 。本文基于有限元軟件ANSYS，先通過結構分析計算出不同觸頭壓力下的接觸面積，以此為基礎分析不同觸頭壓力和不同短路電流對電動斥力的影響。

2 接觸系統結構分析

動靜觸頭的實際接觸面積很小，且離散分布，一般取一等效的中心圓形導電斑點來計算。實際的接觸面積與觸頭壓力、觸頭的幾何形狀和材料有關，運用傳統計算接觸半徑的公式估算彈塑性變形的量，存在著誤差。而在運用有限元進行結構分析時，由于可以根據觸頭的實際結構建立模型，材料屬性包含了應力應變曲線，而且根據要求可以施加不同的載荷，因此可以較好地分析觸頭的實際彈塑性變形，能較為準確地求出接觸半徑［5］，結構分析的流程如圖1所示。圖2為動靜觸頭結構分析的有限元模型，由于要對接觸體進行分析，所以在可能的接觸區域建立接觸對。觸頭具有軸對稱性，因此只需建立1/2的二維模型。

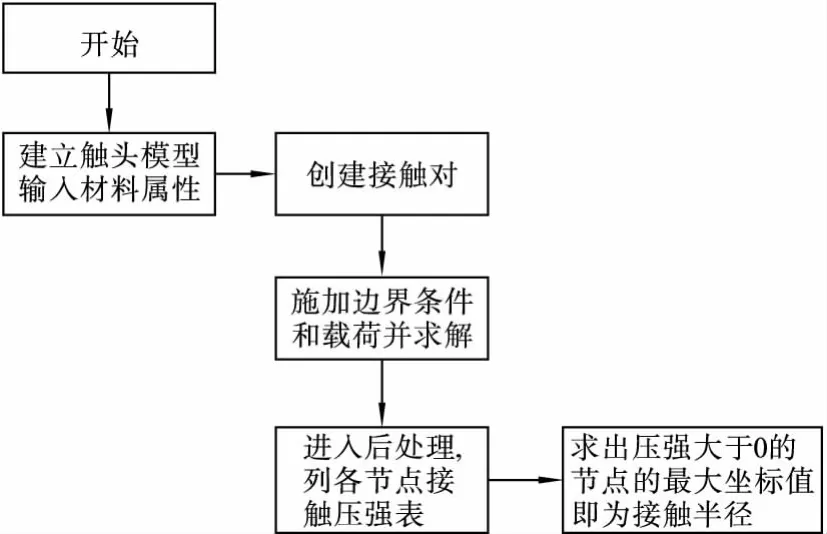
圖1 求解接觸半徑的ANSYS結構分析流程圖

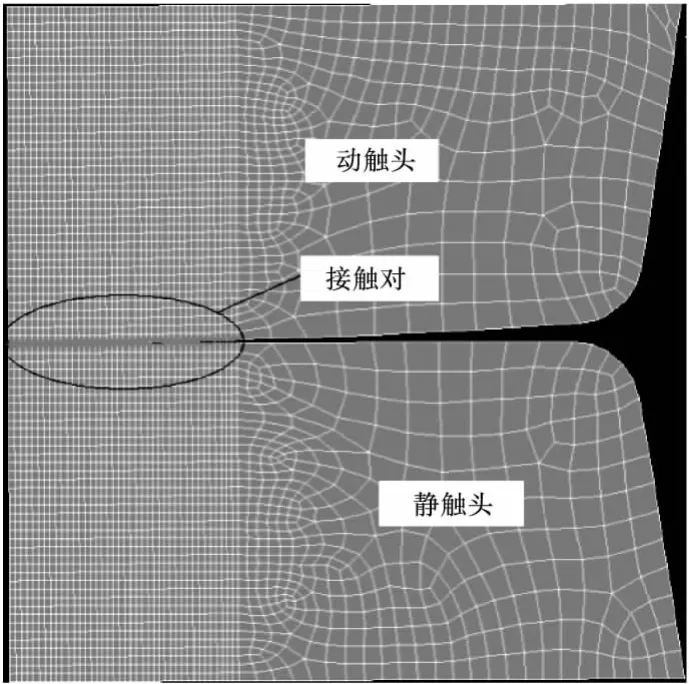
圖2 觸頭結構分析的有限元模型

由有限元結構仿真分析和公式法計算得到的接觸力與接觸半徑關系如表1所示。公式法計算采用工程上常用的計算公式:

其中是引入的參數，用來衡量觸頭表面光滑度和變形程度，其值介于0．3與1之間，接觸表面越光滑，變形越塑性，ξ越接近于1，反之則越接近于0．3。

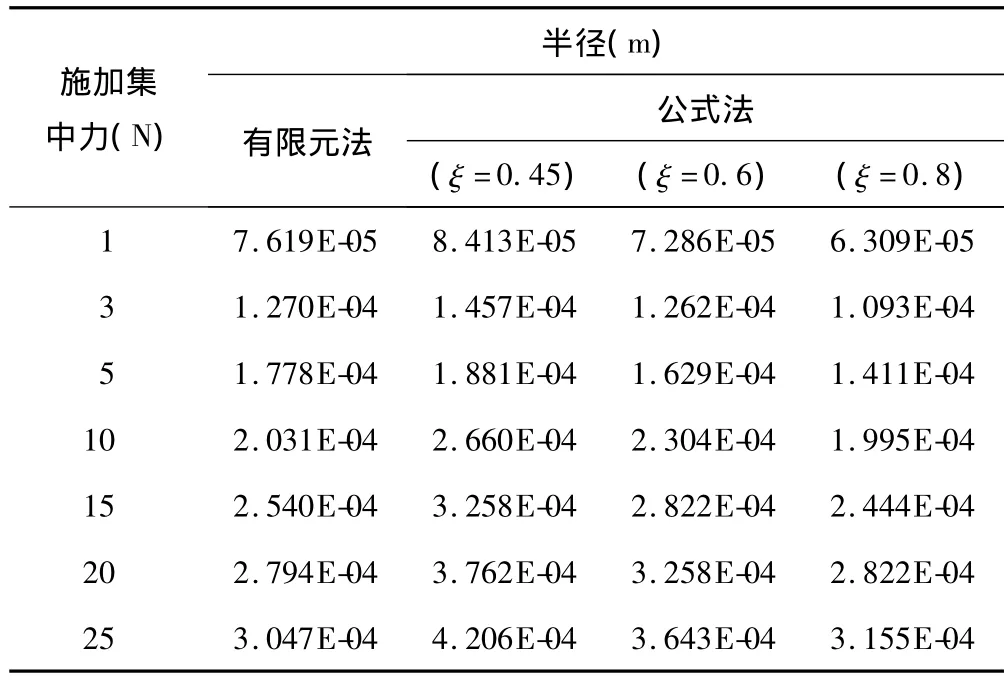
表1 有限元法與公式法計算得到的接觸半徑的比較

利用三維制圖軟件建立接觸系統模型如圖3所示。將該模型導入ANSYS中并建立包含接觸系統的外圍空氣體模型。本文所研究繼電器動觸頭為球面，靜觸頭為圓柱面，建模時使球面與圓柱面相切，以切點為圓心建一圓周并向球面拉伸成圓柱型導電橋以模擬接觸面［2，6］，圓柱的半徑據上表得出，此模型可以模擬在實際接觸區域的電流線收縮效應。

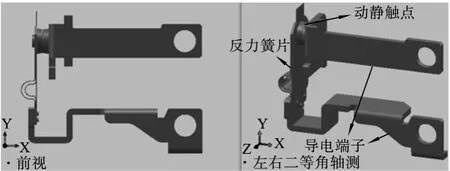
圖3 接觸系統的三維模型

3 電磁耦合場分析及電動力計算原理

本文利用ANSYS的電流傳導—靜磁耦合分析進行電動力的計算。首先對接觸系統進行電流傳導分析。計算出導電體各個部分的電流密度，再將計算結果載入靜磁分析中作為載荷。圖4為電流傳導分析得到的接觸系統電流密度分布矢量圖，從圖中可以看到在接觸區域有強烈的電流收縮效應。通過靜磁分析可以計算出每個單元的電動力矢量。所分析的接觸系統可動部件主要為動觸頭和與之相聯的簧片，只有作用在這兩部件上的力才能導致觸頭斥開。由于Holm力本身也是洛倫茲力，因此電動斥力均可按照洛倫茲力公式FL=∫∫∫J×BdV進行計算。如圖4所示坐標系，電動斥力只有X軸分量才能使觸頭斥開，并且由于簧片一端固定，因此以力矩的形式來計算，將積分化為單元求和，即:M=∑v1FLx·LY+∑v2FLX·LY，其中v1，v2分別表示簧片和動觸頭，LLX表示網格單元的洛倫茲力的X軸分量，FY表示網格單元質心到簧片固定端的距離的Y軸分量。由于網格單元劃分足夠細，兩者乘積即近似網格單元的斥力力矩。對兩部分所有網格單元進行求和可分別得到兩部分的總斥力矩。

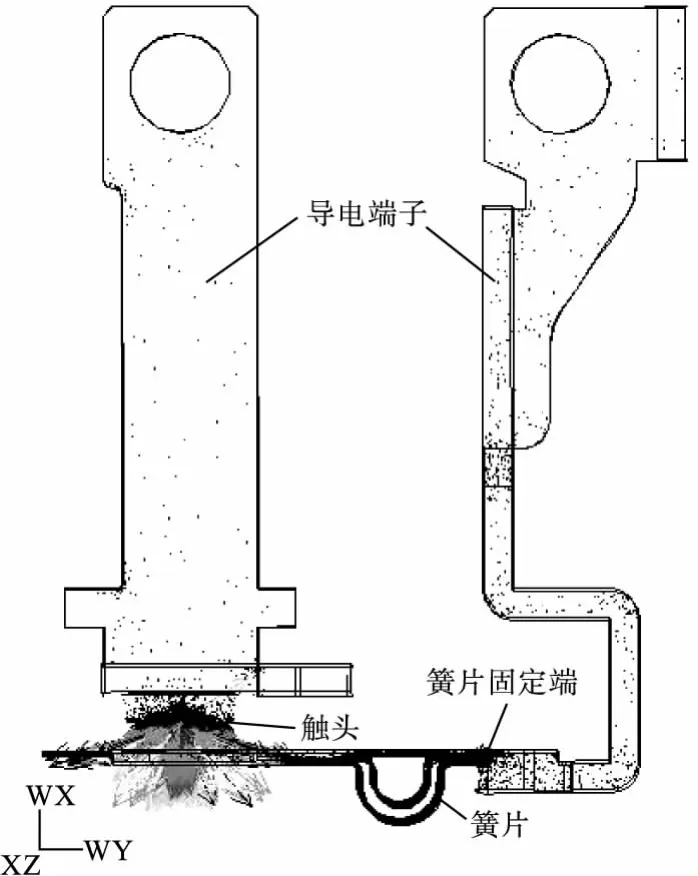
圖4 電流密度分布矢量圖

4 電動力計算及結果分析

4．1 電動力的計算

本文將對不同電流和不同觸頭壓力對電動斥力的影響進行分析，分別用有限元法和公式法對電動斥力進行計算，其中公式法采用以下公式［6，7］:

式中，B為接觸導體截面半徑，單位為mm，由公式(1)得到;F為觸頭壓力，單位為N;H為材料布氏硬度，單位為N/mm2。

設置的分析實驗如下:①根據上述有限元法結構分析計算2．5N觸頭壓力下得到的結果建立電動力分析模型，輸入不同的電流值進行電動力計算和分析。②以繼電器的30倍額定電流即2400A作為有限元模型的輸入載荷，改變接觸半徑進行計算和分析。由于接觸系統為拍合式，兩種情況的計算結果轉化成對簧片固定端的力矩進行比較。

圖5是接觸半徑不變，改變輸入電流所得的仿真和計算結果，圖中的標幺值是以1000A時的有限元仿真結果作為基值進行歸算。

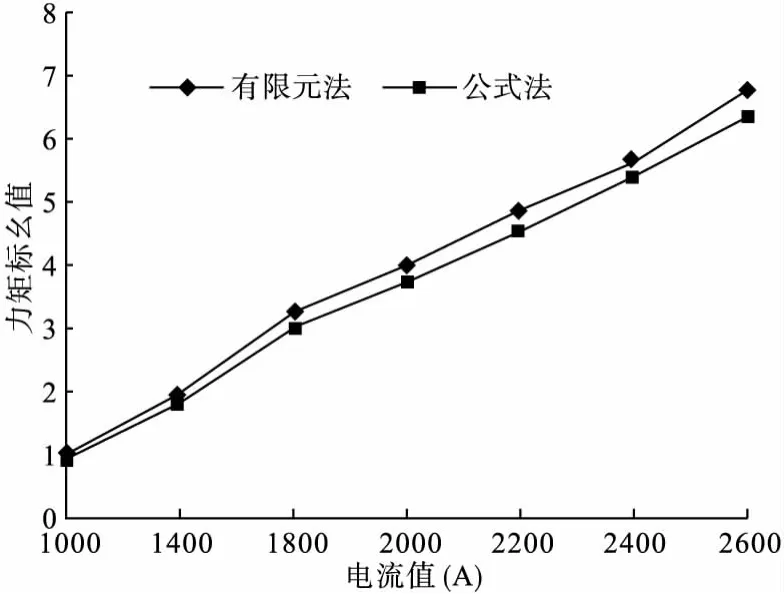
圖5 2．5N觸頭壓力下不同電流的電動力計算結果

圖6是輸入電流不變，改變接觸斑點半徑所得的仿真和計算結果，圖中的標幺值是以接觸半徑為0．102mm時的有限元仿真的結果作為基值進行歸算。

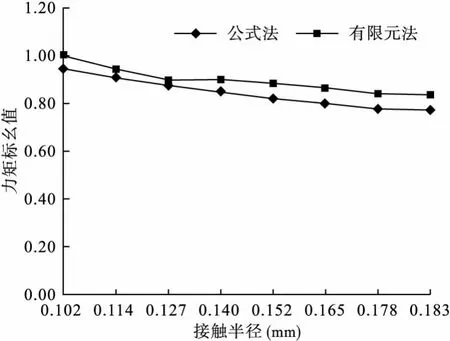
圖6 2400A電流下不同接觸半徑的電動力計算結果

從圖5和圖6可以看出有限元法與公式法的結果比較吻合。

4．2 接觸各部件對電動斥力的影響分析

由于電動斥力來源于簧片的洛倫茲力和觸頭上的Holm力，為研究兩者在總的電動斥力中所占的比重，以2400A作為輸入載荷對不同的接觸半徑下的電動力進行仿真分析，結果如圖7所示。由圖中可以看出觸頭部分的斥力是產生電動斥力的主要原因，隨著觸頭壓力的增大，接觸半徑增加，電流收縮效應對電動力的影響呈減少趨勢。而簧片上電流密度分布與接觸半徑關系不大，在圖中近似水平直線。

根據洛倫茲力公式FL=∫∫∫J×BdV可知，觸頭上的電動力的產生不僅與電流線收縮有關，還與觸頭

上的磁感應強度相關，而作用在觸頭上的磁感應強度主要由觸頭的收縮

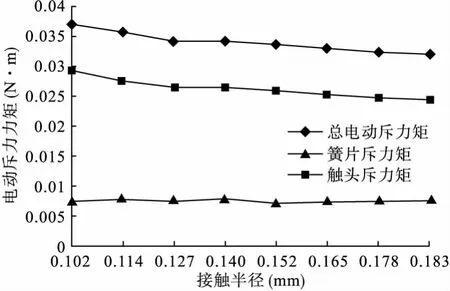
圖7 簧片洛倫茲力、觸頭Holm力和總電動斥力比較

電流和觸頭簧片、導電端子的電流感應而來。為研究觸頭簧片和導電端子對觸頭電動斥力的影響，設計如下仿真分析，即對不同的接觸半徑進行電流傳導仿真，并將結果分兩種情況分別導入到靜磁場分析中:①將接觸系統所有部件的電流仿真結果作為載荷導入到磁場分析中;②只將動靜觸頭的電流仿真結果作為載荷導入。由于電流傳導分析是對整個接觸系統進行，因此能反映真實的電流分布情況。在分別導入靜磁場分析時，兩種情況下動靜觸頭的電流分布是一致的，唯一的區別是其他導電部件上是否加載有電流。這樣就可以較好地分析觸頭簧片和導電端子的影響。結果如表2所示。

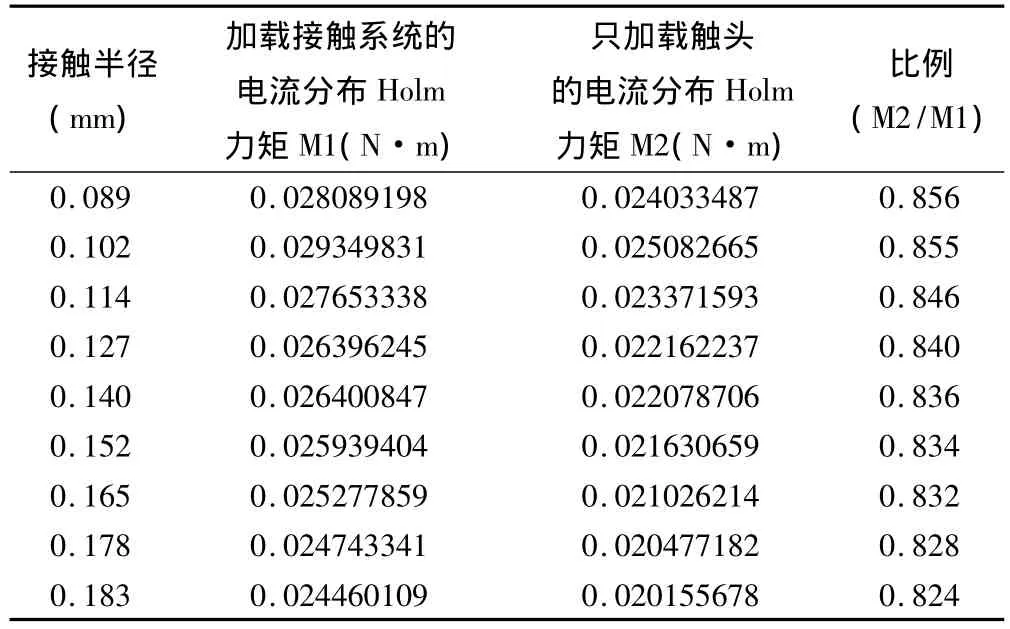
表2 加載接觸系統的電流分布和只加載觸頭的電流分布的Holm力矩仿真結果對比

如表2所示，加載整個接觸系統電流分布所產生的Holm力大于只加載觸頭電流分布兩者所產生的Holm力，表明產生觸頭電動斥力的磁感應強度雖主要來源于觸頭本身的電流線收縮，但周圍導體(如觸頭簧片和導電端子等)的電流在觸頭感生的磁場也不能忽略。如表2中的比例所示，收縮電流與其自身感應的磁場相作用產生的斥力占觸頭電動斥力的百分之八十幾，其余為周圍導體產生的磁場對電動斥力的影響，而且隨著接觸半徑的增加，周圍導體對斥力的影響增大。因此在設計時須考慮導電回路對觸頭可能造成的影響并盡量減少。

4．3 觸頭壓力對電動斥力的影響分析

觸頭上的電動斥力的大小與接觸斑點的面積有關，在材料相同時，接觸斑點的面積取決于觸頭壓力，因此觸頭壓力減少將導致觸頭上的電動斥力增大，當電動斥力大于觸頭壓力時將導致觸頭斥開。為考察觸頭壓力與電動斥力的關系，分別從2N到5N進行觸頭的結構力學分析，求出不同觸頭壓力下的接觸半徑，并以2400A為電流載荷，導入電流傳導—靜磁耦合場進行電動斥力分析計算，結果如圖8所示。

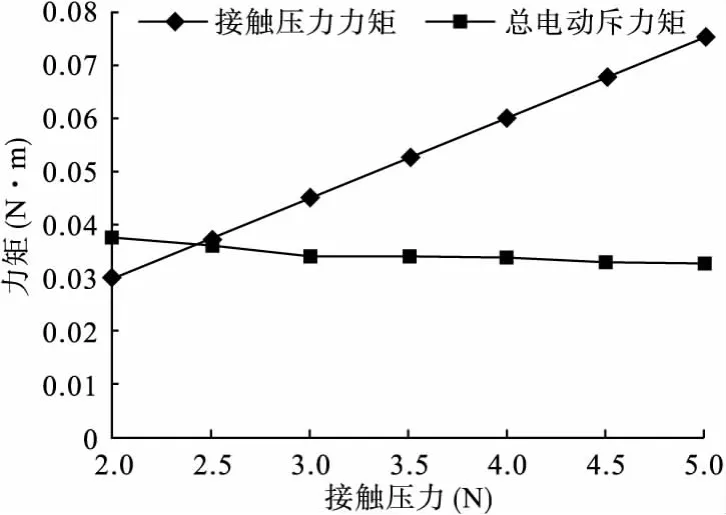
圖8 接觸壓力力矩與電動斥力力矩的關系

從圖中可以看出，當短路電流為2400A，觸頭壓力在2．5N時其力矩與電動斥力力矩已相當接近，此時有可能發生觸頭斥開現象。因此，設計的繼電器時應使觸頭在閉合時有大于2．5N的觸頭壓力，并留有一定的裕值。

5 結論

本文利用ANSYS軟件作為有限元計算工具，對磁保持繼電器的接觸系統進行電動力的仿真計算與影響因素分析，并與傳統工程上運用的公式法進行比較。

通過結果分析與比較可得，不論是結構分析抑或耦合場分析，有限元法與公式法計算結果相近，但有限元法在結構分析中能直接反映觸頭結構和彈塑性變形對接觸半徑的影響，在耦合場分析中能準確計算復雜結構的電流密度和磁感應強度的分布，這都有利于電動力的準確求解和分析。通過對電動力中觸頭Holm力和導體洛倫茲力的分析可知，Holm力是電動斥力的主要成份，但導體的洛倫茲力也不可忽略，而且導體中電流感生的磁場對觸頭Holm力也有一定的影響。

［1］ Monnier，B．Froidurot，C．Jarrige，R．Meyer and P．Testé．A mechanical，electrical，thermal coupled-field simulation of a sphere-plane electrical contact［J］．IEEE NO．2，2005:224 － 231．

［2］ Yoshihiro Kawase and Hiroyuki Mori．3-D Finite Element Analysis of Electrodynamic Repulsion Forces in Stationary Electric Contacts Taking into Account Asymmetric Shape［J］．IEEE NO．2，1997:1994 －1998．

［3］ Yoshihiro Kawase and Hiroyuki Mori．3-D Finite Element Analysis of Repulsion Forces on．

［4］ Contact Systems in Low Voltage Circuit Breakers［J］．IEEE NO．3 1996:1677－1680．

［5］ Tomohiro Ota，Satoshi Suzuki and Katsuhiro Hirata．Dynamic Analysis Method of Repulsion Forces On Current-Carrying Contact Using 3-D FEM［J］．IEEE NO．5，2011:942 －945．

［6］ 李興文，陳德桂，劉洪武，等．觸頭間電動斥力的三維有限元分析［J］．高壓電器，2004(2):53 －55．

［7］ 劉穎異，陳德桂，李興文，等．用三維有限元方法研究影響框架斷路器電動斥力的因素［J］．中國電機工程學報，2005(8):63－67．

Analysis of Electric of Contact System Based on ANSYS Finite Element M ethod

HUANGWei-jie，LAN Tai-shou，LIU Xiang-jun
(Electrical Engineering and Automation College of Fuzhou University，Fuzhou 350108，China)

The electric repulsion force of relay consists of Holm force on the contacts and Lorentz force on the conductors．The safety and the stability ofmagnetic latching relay should be confirmed by the experiment in which the contacts should not be open by the repulsion force caused by the impulse current．In this paper，finite element structural analysis are used to calculate the contact radius of the relay，and then，the current density and magnetic field distribution in the various parts of the relay are calculated by the coupling field analysis to solve the electric repulsion force．Finally，the paper calculates and analyses the repulsion force in different contact pressure and short-circuit current，aswell as the affects of different parts of contact system on the repulsion force．The study will provide the foundation for the improvement of the contact system of the relay．

magnetic latching relay，electric repulsion force，contact radius，finite element analysis

TM58

B

1004－289X(2013)04－0018－05

book=24,ebook=161

2012－10－10