復(fù)合控制模式的長行程納米定位控制系統(tǒng)
張晴,王吶,周浩
(合肥工業(yè)大學(xué)儀器科學(xué)與光電工程學(xué)院,安徽合肥230009)
0 引言
納米定位平臺是微納米三坐標測量機的重要組成部分,為準確定位,本文使用基于BPNN-PID(誤差反向傳播神經(jīng)網(wǎng)絡(luò)PID)的控制器來控制平臺精準定位至納米級。
傳統(tǒng)X-Y 平臺通常是由兩個單軸移動平臺堆疊而成,由于軸與軸之間互相干擾即使單軸具有納米級定位精度,也很難使系統(tǒng)同樣具有納米級定位精度,為此采用符合三維坐標阿貝原則的共平面平臺[1],理論上可完全消除阿貝誤差。
作為閉環(huán)定位控制系統(tǒng)中的平臺驅(qū)動部分,需選用具有長行程兼高分辨力的驅(qū)動器。超音波馬達具有結(jié)構(gòu)緊湊且將多種驅(qū)動模式整合到一個驅(qū)動器中的優(yōu)點,本文采用以色列Nanomotion 公司的超聲波馬達[2]。其使用側(cè)面摩擦力作為驅(qū)動力的機制使得平臺運動穩(wěn)定性對導(dǎo)軌摩擦力變化非常敏感,因而對其控制是一大難點。傳統(tǒng)使用固定參數(shù)的PID 控制器不能克服摩擦力變化帶來的速度振蕩,需用自適應(yīng)性的PID[3]。Zhao 使用Back Propagation(BP)模糊神經(jīng)網(wǎng)絡(luò)控制超音波馬達速度,但只給出了仿真結(jié)果[4];Seniyu 提出使用BPNN 算法控制超音波馬達速度,但是沒有實際應(yīng)用[5]。本文使用BPNN-PID(Back-Propagation Neural Network PID)來控制以HR4 及AB2[2]驅(qū)動的平臺,以實驗室自行開發(fā)的多自由度傳感器MDFS(Multi Degrees of Freedom Sensor)作為長行程納米定位控制系統(tǒng)中的位移反饋。平臺用在微納米三坐標測量機中,快速逼近目標時的驅(qū)動速度限制在1 mm/s,此連續(xù)運動使用馬達的AC 模式,同時使用BPNN-PID 控制速度。微米級行程使用馬達的Gate 模式,由于Gate 模式是離散的小步驅(qū)動,只需使用簡單的比例PID 來控制步長。最后使用DC 模式做精確的位移調(diào)整,此時重新使用BPNN-PID 來控制,與AC 模式不同的是此時的控制量是位移,通過BPNN-PID 調(diào)整驅(qū)動電壓以抵抗應(yīng)力釋放和壓電陶瓷元件的蠕變效應(yīng),從而鎖定平臺的位置。
1 納米定位控制系統(tǒng)組成與結(jié)構(gòu)
該運動控制系統(tǒng)由激勵系統(tǒng)(兩個超音波馬達),位移量測系統(tǒng)(兩個多自由度傳感器MDFS)和自調(diào)式神經(jīng)網(wǎng)絡(luò)PID 構(gòu)成。編程環(huán)境使用Borland C++ Builder 6.0,輸入輸出信號經(jīng)由NI(National Instrument Co.)公司PCI 系列采集卡進行A/D,D/A 轉(zhuǎn)換,圖1 為控制系統(tǒng)原理圖。
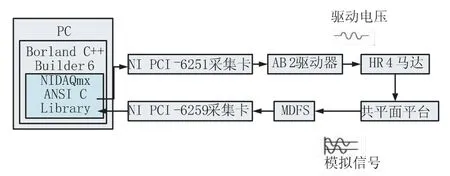
圖1 基于BP 神經(jīng)網(wǎng)絡(luò)的二維共平面平臺控制系統(tǒng)原理圖
單顆壓電陶瓷(PZT)元件的原理如圖2(a)所示:在PZT 上表面置有四個電極A,B,C,D,每個電極為PZT 約四分之一的上表面積,而PZT 的下表面覆蓋單一電極,斜對角線的電極(A 和C,B 和D)由導(dǎo)線相互連接。激勵電壓使得兩組電極一組伸長,一組縮短時,將使PZT 元件產(chǎn)生彎曲模態(tài)運動,而兩組同時伸長或縮短時,則產(chǎn)生伸長模態(tài)。將與PZT 元件共振頻率相同的39.6 kHz 的電壓作用在其上時,會激發(fā)PZT 元件同時產(chǎn)生彎曲與伸長模態(tài)的運動,此兩種狀態(tài)合成為一橢圓形運動軌跡,通過PZT 元件上端的突出部分與導(dǎo)軌在一定預(yù)壓作用下通過摩擦力驅(qū)動平臺產(chǎn)生直線運動。若是其中一組固定,對另一組施以弦波電壓時,則會往單一方向移動,由此進行方向控制。為提高馬達驅(qū)動動力以增加穩(wěn)定性及保持力的延續(xù)性,Nanomotion 并聯(lián)四顆PZT 元件組成HR4。
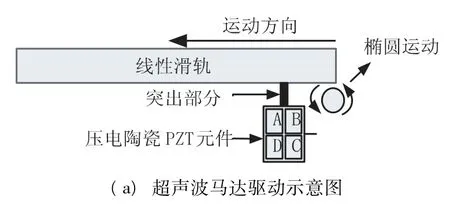

圖2 超聲波馬達HR4 工作原理
HR4 馬達及其驅(qū)動器AB2 提供三種驅(qū)動模式[2]。AC 模式下,HR4 驅(qū)動平臺連續(xù)運動,可以看作是壓電陶瓷元件無數(shù)次高頻離散驅(qū)動的合成。距離目標點較遠時,用此模式使平臺以約1 mm/s 的速度快速逼近物體,但HR4 是通過側(cè)面摩擦力直接驅(qū)動平臺,移動平臺與導(dǎo)軌間變化的摩擦力將影響速度穩(wěn)定性,尤其平臺在起動時,摩擦力特性比較復(fù)雜,速度會有過沖,需使用具有自適應(yīng)性的BP 神經(jīng)網(wǎng)絡(luò)控制速度。使用AC 模式驅(qū)動平臺逼近目標點至5 μm 后切換至Gate 模式,HR4 驅(qū)動平臺產(chǎn)生20 ~50nm 的離散小步驅(qū)動,使用簡單的算法對步距進行控制,只需控制步長落在DC模式可以補償?shù)姆秶鷥?nèi)即可。Gate 模式驅(qū)動平臺逼近目標點30 nm 后切換至DC 模式,補償Gate 模式驅(qū)動結(jié)束后殘留的納米級的定位誤差。該模式下,HR4 類似于傳統(tǒng)的壓電陶瓷驅(qū)動器工作,直接利用壓電效應(yīng)的彎曲模態(tài)。AB2 驅(qū)動器的DC 模式接受±10V 的電壓按特性曲線轉(zhuǎn)換為對應(yīng)的微量位移。實際推動平臺時,馬達推動量受到導(dǎo)軌不恒定阻力與摩擦力的影響,推動量不再遵循理想特性曲線,需使用具有自適應(yīng)性的BPNN-PID 以位移作為控制量,調(diào)整驅(qū)動電壓。達到目標點后若需長時間鎖位,由于壓電陶瓷本身蠕變特性及機械元件應(yīng)力釋放,若驅(qū)動電壓不變,平臺會發(fā)生位移漂移,仍需使用BP 神經(jīng)網(wǎng)絡(luò)控制來調(diào)整電壓以準確鎖位。
為實現(xiàn)納米級精度定位控制,需要高精度的傳感器來作為位移反饋。該工作臺中采用了邁克爾遜干涉儀加自準直儀構(gòu)成的高精密多自由度量測系統(tǒng)MDFS[6],其中邁克爾遜干涉儀的參考光直接打在固定在平臺上的的移動反射鏡上,因此便可直接量測精密平臺單軸移動時的移動距離與平臺移動時其角度的俯仰與偏擺量,受限于相干長度,MDFS 的行程可達25 mm,分辨力優(yōu)于1 nm,測量重復(fù)性精度在10 nm以內(nèi)。測量結(jié)構(gòu)示意圖及實物圖如圖3所示,兩軸位移感測器(MDFS)的激光器光軸處于同一高度,并交于平臺中心,理論上完全符合阿貝原則。結(jié)構(gòu)中,由于傳感器MDFS 和超音波馬達分別固定于平臺兩側(cè),馬達產(chǎn)生的振動不會傳到感測端。
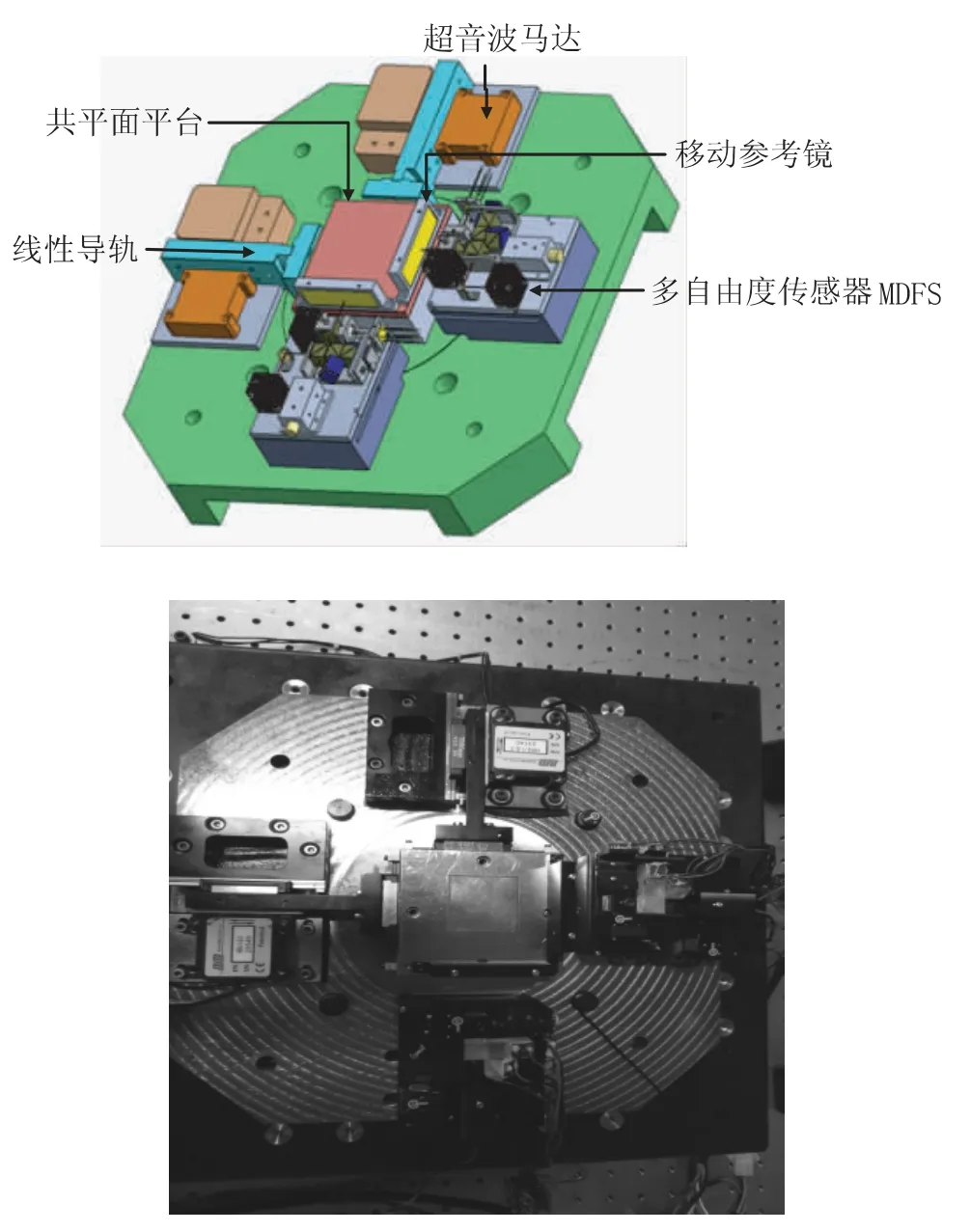
圖3 量測系統(tǒng)示意圖及實物圖
2 基于BP 神經(jīng)網(wǎng)絡(luò)的PID 控制原理
在本控制系統(tǒng)中,使用具有線性特性的PID 控制器。它根據(jù)被控量的給定值r(k)與輸出值y(k)構(gòu)成控制偏差e(k)=r(k)-y(k),其中AC 模式下被控量是速度,GATE 模式下是步距,DC 模式下是位移,將偏差的比例(P)、積分(I)、微分(D)通過線性組合算出下一次驅(qū)動電壓。數(shù)字式PID 控制算法表達式如下式所示:
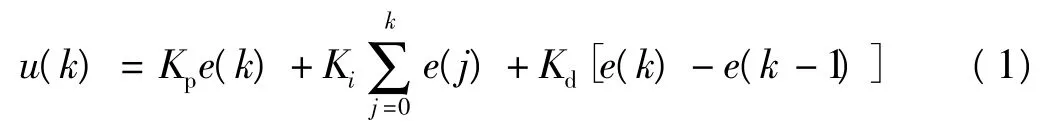
2.1 傳統(tǒng)PID 控制
傳統(tǒng)PID 控制使用恒定的KP,KI,KD參數(shù),在參數(shù)的調(diào)整上需反復(fù)實驗找出最佳值。如在AC 模式下控制速度時,在平臺啟動瞬間,摩擦力從最大靜摩擦力轉(zhuǎn)為滑動摩擦力,摩擦力特性比較復(fù)雜,通過不斷調(diào)整PID 參數(shù),即時是較好的控制效果也需要經(jīng)歷一段震蕩才能進入穩(wěn)態(tài)。且當現(xiàn)場條件改變,如導(dǎo)軌鎖緊程度不同帶來的摩擦力變化,將導(dǎo)致原設(shè)定的PID 參數(shù)不能再進行有效的速度控制。
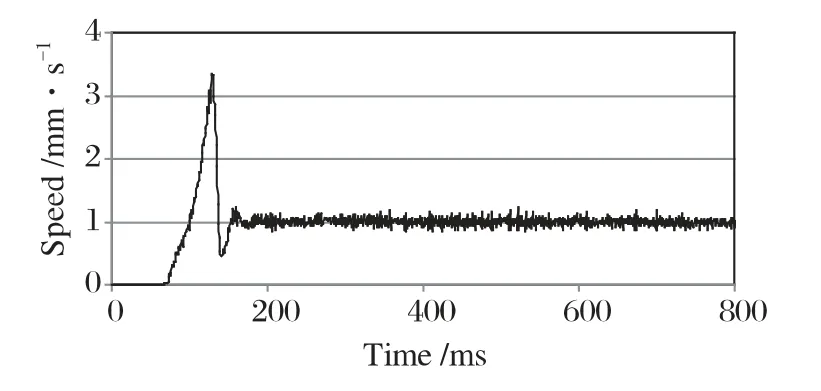
圖4 傳統(tǒng)PID 調(diào)整到合理的PID 參數(shù)控速效果
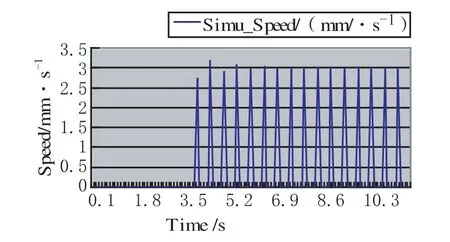
圖5 導(dǎo)軌鎖緊程度改變時,原先的PID 參數(shù)不再適用
2.2 基于BP 神經(jīng)網(wǎng)絡(luò)的PID 控制
為了改善上述傳統(tǒng)PID 的不足,在本納米定位控制系統(tǒng)中采用誤差反向傳播神經(jīng)網(wǎng)絡(luò)(BPNN)來實時調(diào)整PID 控制參數(shù)。BP 神經(jīng)網(wǎng)絡(luò)的具體算法參考文獻[5-6]。
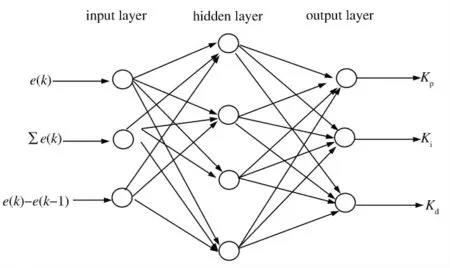
圖6 BP 神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)
圖6所示為BP 神經(jīng)網(wǎng)絡(luò)的結(jié)構(gòu),通過BPNN 算法,將被控量偏差e(k)作為學(xué)習(xí)量,來自動調(diào)整PID控制器的三個參數(shù)Kp,Ki,Kd。它由輸入層、隱藏層、輸出層組成。輸入層三個神經(jīng)元的輸入分別為e(k),∑e(k)及e(k)-e(k-1),對于隱藏層和輸出層來說,每個神經(jīng)原j 的輸入netjn和輸出yjn如公式(2)所示[7]。
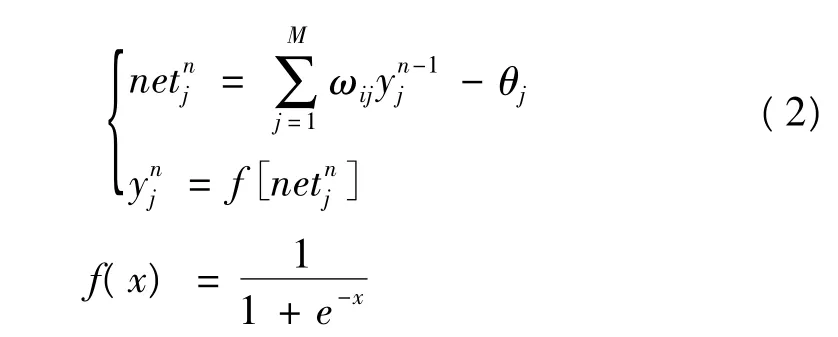
式中:θj是各神經(jīng)原的閾值;ωij是前一層到后一層的連接權(quán)。輸出層中三個神經(jīng)原的輸出量即為PID 控制器的比例系數(shù)Kp、積分系數(shù)Ki、微分系數(shù)Kd。
BPNN 實時修正輸入層到隱含層以及隱含層到輸出層之間的連接權(quán)ωij,算法依據(jù)為使用最快速度下降(最速下降法)以使其指標函數(shù)最小化。
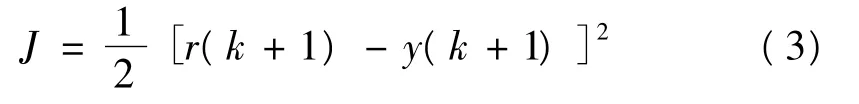
3 實驗
為驗證以上BPNN-PID 控制系統(tǒng)的性能,設(shè)計如下兩部分實驗。
首先,假設(shè)MDFS 的測量精度準確可靠,驗證AC 模式下控速和DC 模式下準確定位。圖7 為BP 神經(jīng)網(wǎng)絡(luò)控制效果,實驗表明在AC 模式下控速時,BP 神經(jīng)網(wǎng)絡(luò)可成功消除平臺起動時的速度過沖,并能在全行程中保持穩(wěn)速運動。用Gate 模式的步進運動來過渡到DC 模式可調(diào)整的距離。圖7(b)顯示在Gate 模式控制結(jié)束后,DC 模式驅(qū)動可以迅速讓平臺進入穩(wěn)態(tài)(約0.2 s)
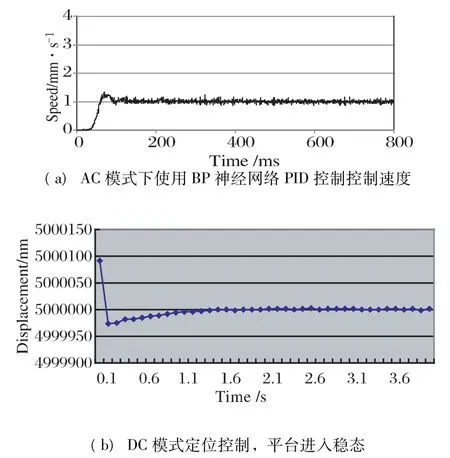
圖7 BP 神經(jīng)網(wǎng)絡(luò)控制效果
其次,驗證MDFS 作為位移反饋時整個系統(tǒng)定位控制的精度,以SIOS SP-2000 激光干涉儀作為標準,當平臺運動到設(shè)定的位置后,讀取MDFS 和SIOS 讀值,兩者之差即為定位誤差,多次重復(fù)可得定位誤差的重復(fù)性。進行單軸比對時的系統(tǒng)結(jié)構(gòu)圖如圖8所示。由于MDFS 的測量線和SIOS 激光干涉儀的測量線并不平行,且導(dǎo)軌非理想直線,因此先對5,10,15 mm 三點進行試驗,所得誤差進行三次多項式擬合,獲得一修正函數(shù),曲線如圖9所示。
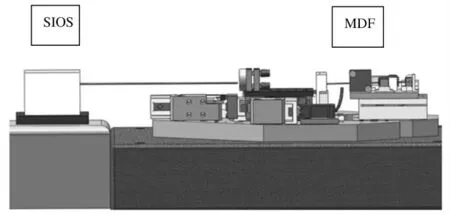
圖8 使用激光干涉儀校正MDFS 精度
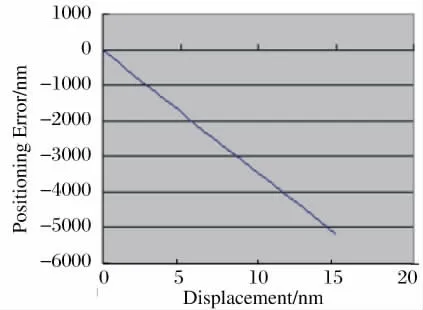
圖9 誤差修正曲線
然后將經(jīng)過激光干涉儀校正后的MDFS 作為定位控制系統(tǒng)的位移反饋,分別對1,5,10,15 mm 四個位置進行定位控制,在驅(qū)動之前用修正函數(shù)計算出修正量對目標位置點進行補償,每點重復(fù)5 次,定位控制效果如表1所示,其中ωn為定位誤差的極限偏差。
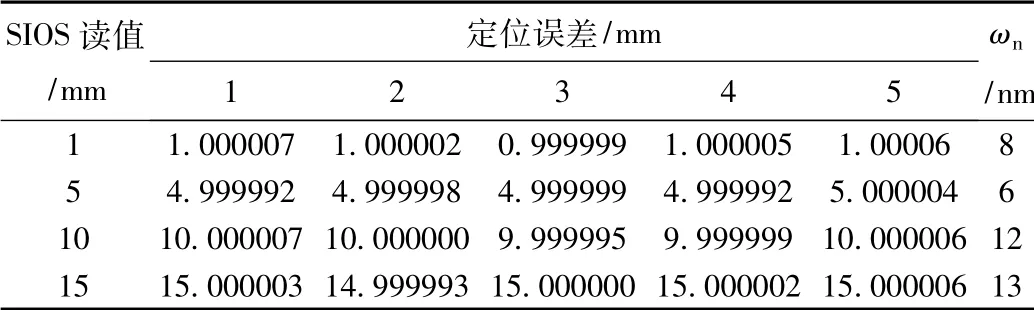
表1 不同行程的定位誤差
4 總結(jié)
本文介紹了一種使用BPNN-PID 控制復(fù)合運動模式下的長行程納米定位系統(tǒng)。針對馬達HR4 及其驅(qū)動器AB2 提供的三種驅(qū)動模式,分別以速度、步距、位移作為控制量,通過使用不同的控制策略達到納米級定位精度。控制系統(tǒng)具有良好的穩(wěn)定性及抗干擾能力,使用經(jīng)SIOS SP-2000 激光干涉儀校準并補償定位誤差后的MDFS 作為位移反饋,補償后在20 mm 的行程內(nèi)定位誤差極差小于15 nm,標準差小于5 nm。結(jié)果證明此平臺定位控制系統(tǒng)可用于微納米三坐標測量機上。
[1]苗晉偉.納米三坐標測量機探頭研制與系統(tǒng)整合[D].合肥:合肥工業(yè)大學(xué),2012.
[2]Nanomotion Ltd.AB2 driver user manual[D].D/N:AB02458000-00 REV.C.2011.
[3]程方.納米三坐標測量機測控系統(tǒng)關(guān)鍵技術(shù)研究[D].合肥:合肥工業(yè)大學(xué),2010.
[4]Zhao X,Chen W,Shi S.Ultrasonic motor's velocity control based on the BP fuzzy neural network with stored information.[C]// proceedings of 1st International Symposium on Systems and Control in Aerospace and Astronautics.2006:1137-1140.
[5]Senjyu T,Miyazato H,Yokoda S,et al.Speed control of ultrasonic motors using neutral network[J].IEEE Trans.Power Electron,1998,13:381-7.
[6]林仲豪.微型三次元量測儀之結(jié)構(gòu)改良與自校正方法之研究[D].臺灣:臺灣大學(xué)機械工程研究所,2012.
[5]Sirisena H,Teng F.Multivariable pole-zero placement self-tuning controller[J].International Journal of Systems Science,1986,17:345-352.
[6]He S Z,Tan S H,Xu F L,et al.,F(xiàn)uzzy self-tuning of PID controllers[J].Fuzzy Sets and Systems,1993,56:37-46.
[7]Wang J,Kang L Y,Cao B G.Neural network PID control of a distributed power generation system based on renewable energy[J].Journal of Applied Sciences,2005,5(10):1772-1776.

