基于正交整體最小二乘平面擬合的點云數據去噪方法研究

葉珉呂，花向紅，陳西江，魏 成

（1.長江科學院工程安全與災害防治研究所，湖北武漢 430010；2.武漢大學測繪學院，湖北武漢 430079；3.武漢大學災害監測與防治研究中心，湖北武漢 430079）

一、引 言

三維激光掃描以其數據獲取速度快、實時性強、精度高及全天候工作等優點而被廣泛應用于工業設計、土木工程及建筑物變形監測等領域，但由于儀器測距、測角誤差、物體反射率、人為操作及遮擋等原因，三維激光掃描獲取的點云數據中存在著大量的噪聲點。這些噪聲點對物體或標靶表面特征點提取的精度有直接影響，不利于配準及三維模型重建等后續工作的進行，因此，獲取點云數據之后必須對其進行去噪處理。

真實場景中含有大量的平面特征，如各種建筑物、道路、隧道及標靶的表面等。對具有平面特征的物體點云數據進行去噪處理，一般使用基于平面擬合的點云數據去噪方法。其原理是首先將物體的三維掃描點云數據進行平面擬合，然后計算各點至擬合平面的距離，最后根據一定的準則刪除點云數據的粗差或異常值，達到點云數據去噪的目的。基于點云數據的平面擬合方法主要包括最小二乘法、特征值法，以及文獻［1］中描述的同時顧及自變量、因變量誤差的整體最小二乘（TLS）方法等。本文根據文獻［2］中提到的二維正交整體最小二乘方法，對其進行三維延伸應用于三維點云數據的平面擬合，并根據點面距離進行點云數據粗差的探測及剔除，通過對比分析及實例驗證，表明該方法具有更高的可行性。

二、點云數據去噪方法

1.最小二乘平面擬合去噪法

最小二乘擬合法假設x、y為自變量，且不含誤差，z為因變量，在包含誤差的情況下解算平面參數，其平面模型為

式中，a、b、c為擬合平面待求參數。具體步驟如下:

1）在最小二乘準則VTV=min下，可得擬合平面未知參數估計值

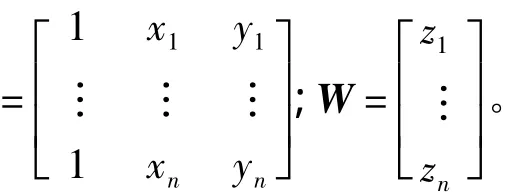
2）計算點云數據集到擬合平面的距離

3）根據測距精度σ/50，計算點集到擬合平面距離di的限差δ

4）判斷di與δ的關系，如果di＞δ，則將di所對應的坐標點刪除，反之則保留。

2.同時顧及x、y、z誤差的TLS平面擬合去噪法

文獻［1］中提出了二維同時顧及自變量、因變量誤差的整體最小二乘方法，將其延伸為三維形式，其平面模型為

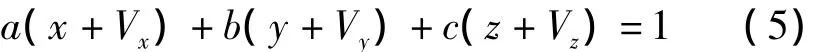
式中，a、b、c為擬合平面待求參數。

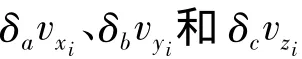
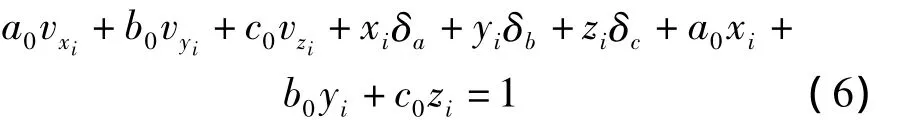
具體步驟如下:

1）在VTV=min下，可得擬合平面未知參數估計值

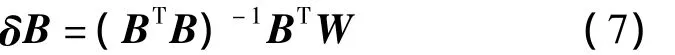
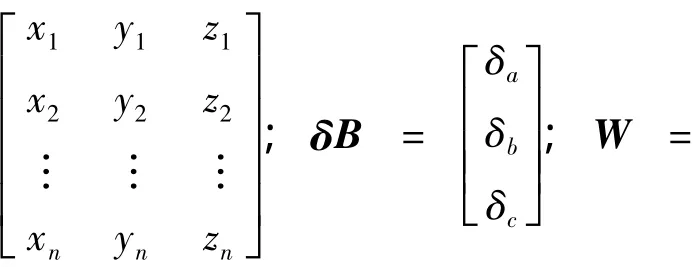
2）計算點云數據集到擬合平面的距離

步驟3）、4）與第一節中步驟3）、4）一致。

3.正交整體最小二乘平面擬合去噪法

正交整體最小二乘以點到平面的正交距離平方和最小為準則，同時顧及了因變量和自變量的誤差［3］。本文將文獻［2］中提出的二維模型延伸為三維形式，其平面模型為

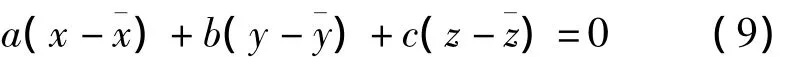
具體步驟如下:

1）構造矩陣M，計算MTM。M形式為

2）對MTM進行特征值分解，取最小的特征值所對應的特征向量作為未知參數a、b、c的值。

3）計算點云數據集到擬合平面的距離

計算限差δ及根據限差去除噪聲點的步驟與第一節中步驟3）、4）一致。

三、試驗與結果分析

使用Riegl三維激光掃描儀獲取一圓形標靶的點云數據，其左視圖如圖1所示，共由6251個點組成。由圖1可以看出，由于儀器測距誤差、測角誤差及物體反射率等原因，該點云存在大量“脫離”標靶表面的噪聲點。標靶定位是精確配準的關鍵，因此必須去除影響標靶中心坐標提取的噪聲點。分別使用上述3種方法進行平面擬合去噪，相應程序在Visual Studio 2010環境下實現，其結果如圖2～圖4所示，比較結果見表1。

圖1 原始點云數據

圖2 最小二乘擬合去噪

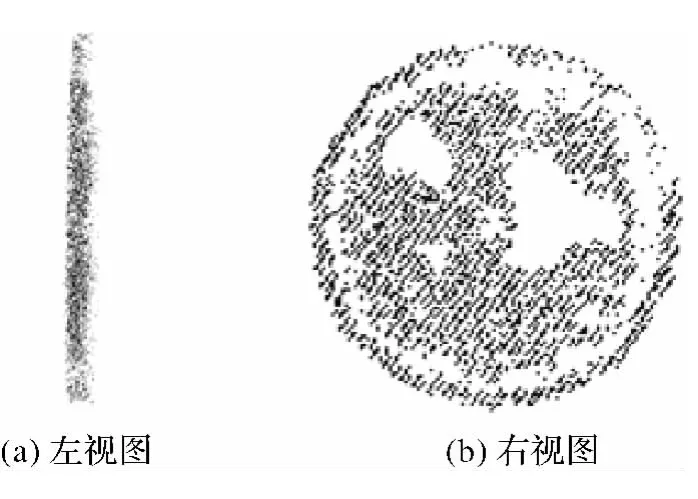
圖3 同時顧及x、y、z誤差的TLS擬合去噪

圖4 正交整體最小二乘擬合去噪

表1 3種方法結果比較

從圖2及表1可以看出，最小二乘擬合法是在假設自變量不含誤差、因變量包含誤差的情況下解算平面參數，但實際上點云數據獲取時x、y、z3個方向均存在誤差。最小二乘法以觀測值殘差平方和極小為準則，忽略了自變量的誤差，擬合結果使得擬合平面沿一個方向與實際平面最佳逼近，因此當點云數據存在粗差或異常數據點時，最小二乘法將會產生錯誤。如圖2所示，最小二乘擬合去噪法不僅沒能準確去除噪聲，而且刪除了較多非噪聲點。

從圖3、圖4及表1可以看出，同時顧及x、y、z誤差的TLS擬合法及正交整體最小二乘擬合法都能夠同時顧及因變量和自變量的誤差，平面擬合精度較高，去噪準確，效果顯著。但兩種方法相比，后者去噪后標靶表面幾乎沒有噪聲點存在，其左視圖呈現為一光滑平面，前者去噪后標靶表面依然存在少量噪聲點，這也可從刪除噪聲點個數及σ看出。原因是由于同時顧及x、y、z誤差的TLS擬合法在形成條件方程時省略過多的誤差因子δv，從而造成了誤差偏執現象；而正交整體最小二乘法是從離散點到平面的最短距離為基準對參數進行解算，避免了由于計算不方便而省略誤差因子δv，因此具有更高的擬合精度，而且該方法算法簡單，計算效率高，更易于實現，具有更高的可行性。

四、結束語

本文根據文獻［2］中提到的二維正交整體最小二乘方法，對其進行三維延伸應用于三維點云數據的平面擬合，并根據點面距離進行點云數據粗差的探測及剔除。通過與傳統方法進行對比分析及實例驗證，表明該方法算法簡單，去噪精度高，具有較高的可行性。該方法適用于各種具有平面特征的物體點云數據去噪，具有廣泛的適用性。

［1］ 魯鐵定，陶本藻，周世健.基于整體最小二乘法的線性回歸建模和解法［J］.武漢大學學報:信息科學版，2008，33（5）:504-507.

［2］ 張賢達.矩陣分析與應用［M］.北京:清華大學出版社，2004.

［3］ 丁克良，歐吉坤，趙春梅.正交最小二乘曲線擬合法［J］.測繪科學，2007，32（3）:17-19.

［4］ 蔡來良，吳侃，張舒.點云平面擬合在三維激光掃描儀變形監測中的應用［J］.測繪科學，2010，35（5）:231-232.

［5］ 魯鐵定，周世健，張立亭，等.基于整體最小二乘的地面激光掃描標靶球定位方法［J］.大地測量與地球動力學，2009，29（4）:102-105.

［6］ 官云蘭，程效軍，施貴剛.一種穩健的點云數據平面擬合方法［J］.同濟大學學報:自然科學版，2008，36（7）:981-984.

［7］ 官云蘭，劉紹堂，周世健，等.基于整體最小二乘的穩健點云數據平面擬合［J］.大地測量與地球動力學，2011，31（5）:80-83.

［8］ 武漢大學測繪學院測量平差學科組.誤差理論與測量平差基礎［M］.武漢:武漢大學出版社，2003.

［9］ 張毅.地面三維激光掃描點云數據處理方法研究［D］.武漢:武漢大學，2008.

［10］ SCHAFFRIN B.A Note on Constrained Total Leastsquares Estimation［J］.Linear Algebra and Its Applications，2006，417（1）:245-258.