經驗公式在家電仿真設計與研究中的應用

蔣皓靜 馮靜 吳曉麗

（中國家用電器研究院 北京 100176）

在進行家用電器的仿真設計與研究時，經常需要根據相關變量的實測數據和歷史資料建立變量間關系的數學表達式，進行預測與分析。例如在研究冰箱蒸發器溫度分布規律的模擬，溫度場和流場的仿真，電機繞組的溫升測定等。從一組實驗數據出發，尋求函數的近似表達式，這個近似表達式就稱為經驗公式。

1 最小二乘法基本原理

為得到經驗公式需要進行數據擬合。數據擬合的具體作法是：對給定數據(x，y ) (i=0,1,…,m)，在取定的函數類Φ中，求p(x)∈Φ，使誤差：r=p(x)-y (i=0,1,…,,m)的平方和最小，即：

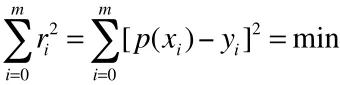
從幾何意義上講，就是尋求與給定點(x，y)(i=0,1,…,,m)的距離平方和為最小的曲線y=p(x)（圖1）。函數p(x)稱為擬合函數或最小二乘解，求擬合函數p(x)的方法稱為曲線擬合的最小二乘法。

2 多項式擬合原理

假設給定數據點(x，y) (i=0,1,…,,m)，Φ為所有次數不超過n(n≤m)的多項式構成的函數類，現求,使得：

當擬合函數為多項式時，稱為多項式擬合，滿足式（1）的p (x)稱為最小二乘擬合多項式。特別地，當n=1時，稱為線性擬合或直線擬合。

式（3）或式（4）稱為正規方程組或法方程組。

可以證明，方程組（4）的系數矩陣是一個對稱正定矩陣，故存在唯一解。從式（4）中解出a(k=0,1,…,n )，從而可得多項式：

可以證明，式（5）中的p (x)滿足式（1），即p (x)為所求的擬合多項式。把稱為最小二乘擬合多項式p(x)的平方誤差，記作：

由式(2)可得

在實際應用中，n＜m或n≤m；當n=m時所得的擬合多項式就是拉格朗日或牛頓插值多項式。

3 具體應用舉例

3.1 應用一

某導線在溫度T (℃)時的電阻R(Ω)如表1，電阻R與溫度T有近似函數關系。

由圖2可見，測得的數據接近一條直線，故取n=1，擬合函數為。列表如表2。矩陣方程組為：

解矩陣方程組得：

故得R與T的擬合直線為:

利用上述關系式，可以預測不同溫度時的電阻值。如，由R=0得T=-242.5，即預測溫度T=-242.5℃時，此導線無電阻。

3.2 應用二

冰箱中蒸發器的形式、位置和溫度對冰箱的性能和食品的保藏有著重要的影響。蒸發器溫度邊界條件的指定也有重要意義。在默認情況下通常指定壁面溫度為常數，而實際上蒸發器表面的溫度往往沿著高度方向有比較大的變化。其中一組數據如表3所示。

由圖3取n=2，設擬合曲線方程為：

得正規方程組：

解得：

故擬合多項式為：

由此可知在冰箱間室內上下溫度差較大,存在著不利于儲存食物的問題（見圖3）。

4 結語

本文對研究中的實際問題建立數學模型，所用原始數據容易獲得，采用數值分析方法簡便可靠，運用所得到的經驗公式進行預測分析對于設計與研發有指導作用。

表1 導線在溫度T(℃)時的電阻R(Ω)

表2 應用一測試數據

表3 蒸發器表面溫度

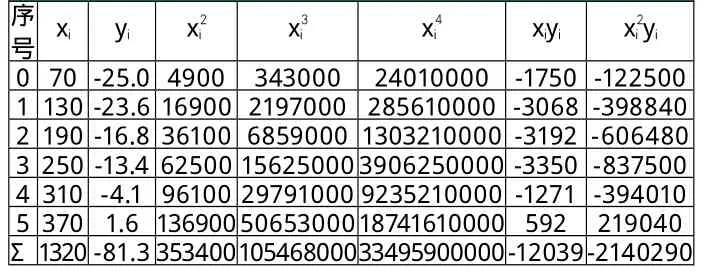
表4 應用二測試數據

[1] 于楠.用于直冷式和間冷式家用冰箱性能預測的數學模型[J].制冷技術,2011，04

[2] 吳小華. 冰箱冷藏室溫度場和流場的仿真與優化[J].北京石油化工學院學報, 2006，03

[3] 楊沫.家用冰箱冷凍、冷藏室溫度場的數值計算[J].制冷學報, 1991,04