考慮固液范德華力作用的微圓管流動數學模型

王小鋒，朱維耀，鄧慶軍，隋新光，婁 鈺，張雪齡

（1．北京科技大學土木與環境工程學院，北京 100083； 2．大慶油田有限責任公司第一采油廠，黑龍江大慶163453）

考慮固液范德華力作用的微圓管流動數學模型

王小鋒1，朱維耀1，鄧慶軍2，隋新光2，婁 鈺1，張雪齡1

（1．北京科技大學土木與環境工程學院，北京 100083； 2．大慶油田有限責任公司第一采油廠，黑龍江大慶163453）

細小孔隙喉道下流體流動呈非線性流動，達西定律不適用，非線性流動的機理認識不清．在現有微尺度流動實驗和理論基礎上，分析影響多孔介質中流體流動的微觀力種類和作用范圍及對流動的影響，建立考慮固液間范德華力的圓管流動數學模型．結果表明：對比泊肅葉流動下的速度分布和平均流量，隨著微管尺寸的減小，固液間的范德華力作用增大，流體在微管內的流動規律影響也增大，因此固液間范德華力作用在細小孔隙流動中不可忽略．

多孔介質；微觀力；范德華力；速度分布；平均流量

0 引言

隨著微機械系統的發展，研究人員對于微尺度下的流動問題有一定認識，油層巖石孔隙尺寸屬于微尺度范疇，因而，進一步研究微尺度下流體的運動規律對于油田開發具有重要意義［1—5］．Gad E H在實驗中觀察到流動的微尺度效應；Pfahler J等進行微觀流動實驗，研究表明流體流動偏離N—S方程預測的理論值［6—7］；Li Qingren，Qu Weilin等在高為14．1，28．2，40．5μm的硅槽中進行水和KCl水溶液的流動實驗，研究表明水的極性是產生微尺度下流動偏離N—S方程的原因［8—9］；武東健等［10］建立水在固壁邊界條件和滑流邊界條件下的阻力因數和速度分布模型，研究表明流體在直徑小于幾百微米的微管中流動特性，用經典流體理論解釋圓微管中的牛頓流體的層流和電解質流動，實驗與理論出現偏差［11—16］，發現管壁與流體之間的微觀力作用是造成這一結果的主要原因［13］．

目前，考慮微觀力作用的微管流動模型鮮見，因此，筆者分析微管內的微觀力作用，研究范德華力對流體在微圓管流動產生的影響，建立固體管壁與流體間范德華力作用下的速度和平均流量模型，并對微圓管內流體的流動進行模擬和分析，為認識和探究多孔介質細小孔喉內流體的流動規律提供參考．

1 多孔介質中的微觀力

流體在多孔介質的孔隙和喉道內流動時，由于孔喉的特征尺寸微小，流體流動受管壁與流體間微觀力的影響增大，微觀力不可忽略．微觀力主要包括范德華力、靜電力、表面張力等．

分子間的范德華力包括3個部分，即取向力、誘導力和色散力．取向力是指分子永久偶極矩間的相互作用；誘導力是指分子被電場作用產生極化而形成的偶極矩與永久偶極矩間的相互作用；色散力是指分子瞬時偶極間的相互作用．黏度是分子間范德華力的表征，分子間范德華力越大，黏度越大，分子間范德華力越小，黏度越小．

靜電力是帶電分子或粒子間的作用力，大小與距離的平方成反比，作用距離比范德華力長，在距離小于0．1μm時最為重要，在10μm時仍有影響．在靜電力作用下，壁面與電解質溶液形成雙電層，當溶液受到壓力差驅動時，雙電層內的凈電荷隨溶液運動，產生流動誘導電場，電場作用使微通道雙電層上的凈電荷向溶液流動的反方向運動，使溶液的正向流速減慢．

表面張力是由液體表面層分子引力不均衡引起的．液體界面的分子與液體本體內的分子所受力不同，表層分子比內部水分子儲存多余的自由能，如果要把內部的水分子舉升到水表面上，需要付出能量做功，能量轉化為表面自由能．表面自由能有趨于最小的趨勢，液體表面有自動縮小的趨勢，收縮力即為表面張力．表面張力與溫度、界面性質有關，油層中流體的表面張力影響油層中流體在巖石表面上的分布，對孔隙中毛管力的大小和方向也有影響，表面張力越大，毛管力越大，也影響流體在多孔介質中的滲流規律．

2 微圓管流動數學模型

2．1 假設條件

假設有水相流體在水平放置的微圓管內定常流動，忽略重力影響（見圖1）．圖1把x軸設在管軸上，令r表示由軸心向外度量的徑向坐標，周向和徑向的速度分量為0，微圓管的半徑為R，平行于管軸方向的速度分量為ux（僅僅依賴于r），沿x方向上的壓力梯度為常數，微圓管的長度為L，入口壓力為p1，出口壓力為p2，考慮固體壁面與流體間的范德華力作用．

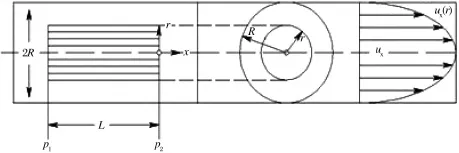
圖1 水平放置的微圓管流體流動示意Fig．1 The scheme of fluid in the horizontal placement micro tube

2．2 黏度方程

當水相在微圓管內流動時，流體與管壁間的范德華力作用使流體間的分子引力增大，因而流體黏度μ增大，假設流體黏度由2部分組成：一是不考慮固液范德華力作用時流體的黏度μ0；二是考慮固液間長程范德華力后增大的黏度，所以流體黏度表示為

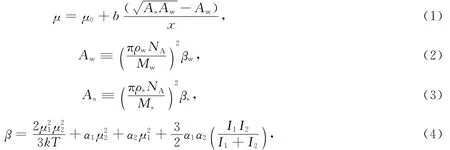
式（1—4）中：b為黏度增加因數；x為到固體壁面的距離；μ1、α1、Ι1分別為水分子的偶極距、極化率和電離能；μ2、α2、Ι2分別為固體表面分子的偶極距、極化率和電離能；Aw、As分別為水和固體管壁的哈默克常數；βw、βs分別為水和管壁的范德華力作用因子；Mw、Ms分別為水和管壁的相對分子質量；ρw、ρs分別為水和管壁的密度；NA為阿伏伽德羅常數；k為波爾茲曼常數．

2．3 運動方程

柱坐標系下N—S方程為

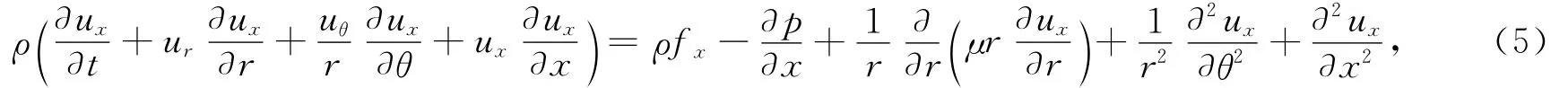
式中：uθ為周向分速度；fx為x方向慣性力；ρ為管內流體密度．

流體在管內定常流動，周向和徑向的速度分量為0，速度u僅僅依賴于r，因而

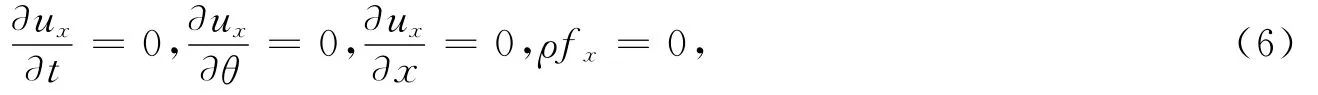
邊界條件為

結合式（1—7），推導可得微圓管內水相速度u為

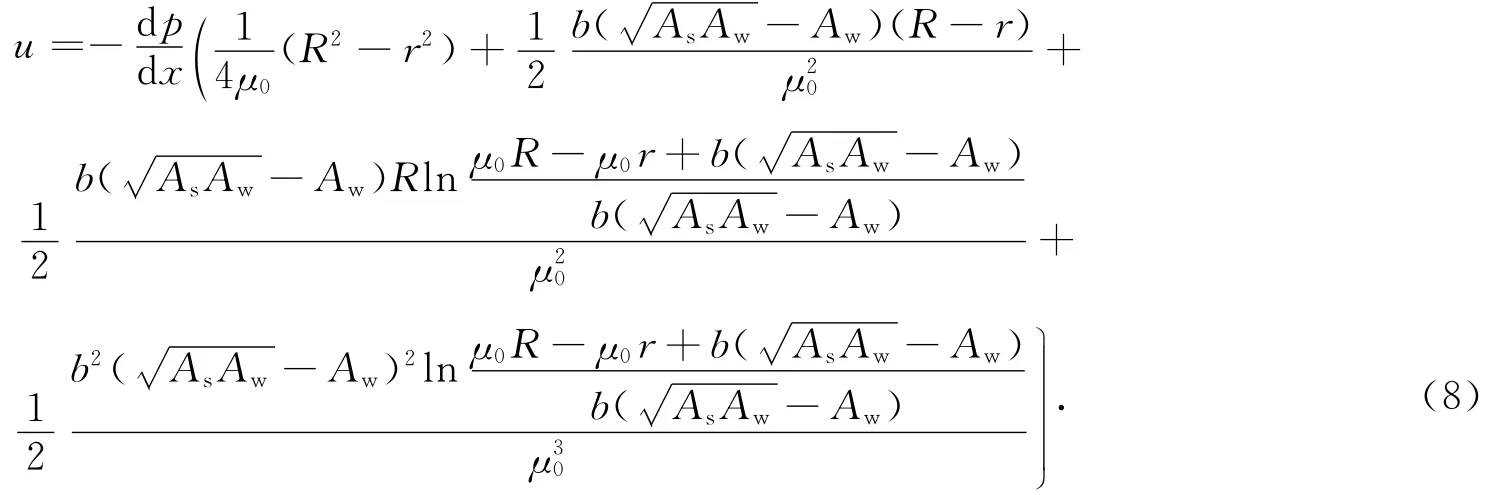
由式（8）積分求得通過微圓管截面的平均流量Q，即

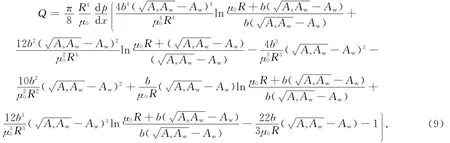
若不考慮固體管壁與流體間范德華力作用時，即AS＝Aw，代入式（9），則式（9）退化為泊肅葉定律形式，即

3 實例分析

3．1 不同管徑下速度分布

根據推導的微圓管內流體的速度分布模型，當流體黏度μw＝1mPa·s，壓力梯度dp／dx＝1×105Pa／m，流體的Hamaker常數Aw＝4．2×10—20J，管壁的Hamaker常數分別取As＝3．6×10—20J，As＝4．2× 10—20J，As＝4．8×10—20J時，模擬流體在不同固液范德華力作用下的速度與泊肅葉流動下的速度，管徑分別取1，100μm，模擬結果見圖2．

由圖2可知，當微圓管半徑在1～10μm時，如果考慮固體管壁與流體間的范德華力作用，那么微管內流體的速度分布明顯低于泊肅葉流動，管徑越小，與泊肅葉流動之間的速度偏離程度越大，固壁面的Hamaker常數越大，與泊肅葉流動的速度偏離程度越大；隨著管徑的增大，分子作用的影響逐漸減小，流體速度也越接近于泊肅葉流動，當管徑達到100μm時，偏離程度已經較小．管徑小于10μm時，速度偏差較大，不能忽略固液間范德華力作用的影響．

3．2 不同管徑下平均流量

根據推導的平均流量模型，當流體黏度μw＝1mPa·s，壓力梯度dp／dx＝1×105Pa／m，流體的Ha—maker常數Aw＝4．2×10—20J，管壁的Hamaker常數分別取As＝3．6×10—20J，As＝4．2×10—20J，As＝4．8×10—20J時，模擬流體在不同固液范德華力作用下的平均流量與泊肅葉流動下的平均流量，管徑分別取0．1～1．0，10～100μm，模擬結果見圖3．

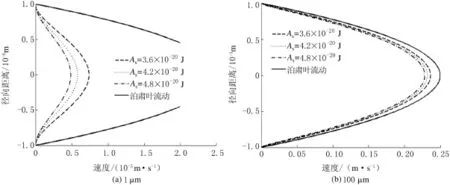
圖2 范德華力作用下不同管徑的速度分布Fig．2 Velocity distribution under different diameters considering van der Waals forces

圖3 范德華力作用下不同管徑的平均流量變化曲線Fig．3 Velocity distribution under different diameters considering micro force

由圖3可知，當管徑在0．1～1．0μm時，如果考慮固體管壁與流體間的范德華力作用，那么微管內流體的平均流量明顯低于泊肅葉流動，管徑越小，與泊肅葉流動之間的平均流量偏離程度越大，固壁面的Hamaker常數越大，與泊肅葉流動的平均流量偏離程度越大；隨著管徑的增大，范德華力作用的影響逐漸減小，流體平均流量越接近于泊肅葉流動，當管徑達100μm時，偏離程度已經較小，當管徑達10～100μm時，幾乎沒有偏離．管徑小于10μm時，平均流量偏差較大，不能忽略固液間范德華力作用的影響．

4 結論

（1）建立考慮固液間范德華力作用的微圓管流動數學模型，推導牛頓流體在微圓管內的速度分布和平均流量模型．

（2）考慮管壁與流體之間的范德華力作用時，對比泊肅葉流動下的流體速度和平均流量，半徑越小，與泊肅葉流動之間的偏離程度越大，管徑在0．1～1μm時，偏離程度很大；半徑越大，范德華力作用的影響逐漸減弱，速度和平均流量越接近于泊肅葉流動，管徑在10～100μm時，偏離程度較小，分子作用幾乎沒有影響．

（3）把巖石孔隙喉道抽象為微圓管，當多孔介質的孔隙喉道尺度小于10μm時，固液間范德華力作用明顯，不可忽略；當孔隙喉道尺度大于10μm時，固液間范德華力作用不明顯，可忽略不計．

參考文獻：

［1］ 劉中春，侯吉瑞，岳湘安．微尺度流動界面現象及其流動邊界條件分析［J］．水動力學研究與進展，2006，21（3）：339—346．Liu Zhongchun，Hou Jirui，Yue Xiangan．Nterfacialphenomena inm icro—scale flowing and its flowing boundary condition［J］．Journal of Hydrodymics，2006，21（3）：339—346．

［2］ 凌智勇，丁建寧，楊繼昌，等．微流動的研究現狀及影響因素［J］．江蘇大學學報：自然科學版，2002，23（6）：1—4．Ling Zhiyong，Ding Jianning，Yang Jichang，et al．Research advance in microfluid and its influencing factors［J］．Journal of Jiangsu University：Natural Science，2002，23（6）：1—4．

［3］ 張穎，王蔚，田麗，等．微流動的尺寸效應［J］．微納電子技術，2008，45（1）：33—36．Zhang Ying，Wang Wei，Tian Li，et al．Scaling effect of micro fluidic systems［J］．Mems Device ＆Technology，2008，45（1）：33—36．

［4］ 張繼紅，王江，趙麗娟，等．單相液體在多孔介質中的電動滲流特性［J］．大慶石油學院學報，2006，21（1）：24—26．Zhang Jihong，Wang Jiang，Zhao Lijuan，et al．Characteristics of electrodynamic seepage flow of one—phase fluid in porous media［J］．Journal of Daqing Petroleum Institute，2002，26（1）：24—26．

［5］ 馬貴陽，杜明俊，李丹．巖石部分潤濕對水驅油藏微觀相態分布的影響［J］．大慶石油學院學報，2006，21（1）：46—50．Ma Guiyang，Du Mingjun，Li Dan．Partial wet of rock impacts on the distribution of water drive reservoir microscopic phase［J］．Journal of Daqing Petroleum Institute，2011，35（2）：46—50．

［6］ Gad E H．The fluid mechanics of microdevices—the freeman scholarlecture［J］．J．of Fluids Engineering，1999，12（1）：5—33．

［7］ Pfahler J，Harley J，Bau H．Liquid transport in micronand submicron channels［J］．Sensors and Actuators，1990，21（23）：431—434．

［8］ Li Qingren，Qu Weilin，Li Dongqing．Interfacial electrokinetic effectson liquid flow in microchannels［J］．Int．J．of Heat and Trans—fer，2001，44（3）：3125—3134．

［9］ Qu Weilin，Mara G M，Li Dongqing．Pressure driven flows in trape—zoidal silicon micro channels［J］．Int．J．of Heat and Transfer，2000，43（4）：353—364．

［10］ 武東健，賈建援，王衛東．微細管道內的流體阻力分析［J］．電子機械工程，2005，21（4）：38—40．Wu Dongjian，Jia Jianyuan，Wang Weidong．Analysis of flow resistance of water in micro channels［J］．Electro Mechanical Engineer—ing，2005，21（4）：38—40．

［11］ Carolyn L R，Li Dongqing．Improved understanding of the effect of electrical double layer on pressure—driven flow in micro channels ［J］．Analytica Chimica Acta，2005，53（1）：15—23．

［12］ Yakov I，Rabinovich．Capillary forces between surfaces with nanoscale roughness［J］．Advances in Colloid and Interface Science，2002，9（6）：213—230．

［13］ Warrier M，Rai A，Schneider R．A time dependent model to study the effect of surface roughness on reactive—diffusive transport in porous media［J］．Journal of Nuclear Materials，2009，39（10）：203—206．

［14］ Anikin Y A，Derbakova E P．Computing of gas flows in micro and nanoscale channels on the base of the boltzmann kinetic equation ［J］．Procedia Computer Science，2010，53（1）：735—744．

［15］ Yakov I R，Joshua J A，Madhavan S E．Capillary forces between surfaces withnanoscale roughness［J］．Advances in Colloid and In—terface Science，2002，9（6）：213—230．

［16］ Celata G P，Cumob M，Mcphaila S，et al．Characterization of fluid dynamic behavior andchannel wall effects in microtube［J］．Inter—national Journal of Heat and Fluid Flow，2006，2（7）：135—143．

TE312

A

2095—4107（2013）05—0085—05

DOI 10．3969／j．issn．2095—4107．2013．05．012

2013—07—23；編輯：關開澄

國家重點基金項目（50934003）；教育部科技專項（FRF—MP—B 12006B）

王小鋒（1985—），男，博士研究生，主要從事油藏數值模擬和滲流理論方面的研究．