艦船輻射噪聲的響度和音色特征模型

曹紅麗 方世良

(東南大學水聲信號處理教育部重點實驗室, 南京 210096)

水下目標識別是現代海戰的重要環節,目標特征的選擇和提取是提高目標識別率的關鍵問題．為了得到有效穩定的識別特征,目前主要利用時域分析、頻域分析、時頻分析以及混沌分形分析等信號處理方法得到的有效特征進行目標識別．由于目標聲學特性的復雜多變性,目標識別率始終無法達到預期要求．實際上,目標識別仍然依賴于聲納員耳聽識別結合機器識別來完成目標識別任務．聲納員聽音判型方法雖然有效,但是聽音判型方法的數學描述很困難．因此,模仿人耳的聽聲過程是一個非常有前景的研究方向．艦船輻射噪聲包括螺旋槳噪聲、機械噪聲和水動力噪聲,其中螺旋槳噪聲是主要噪聲,聲納員就是根據螺旋槳的噪聲進行聽音識別[1]．聲納員的聽音判型是根據心理聲學特征進行識別,心理聲學特征包括響度、音調和音色,其中主要依據響度和音色特征．目前,研究者將響度[2-4]和音色特征應用于水下目標識別[5]中,目標識別率得到了一定的提高,但這些方法沒有考慮艦船輻射噪聲自身的特點,因此建立艦船輻射噪聲的心理聲學特征模型尤為重要．本文研究艦船輻射噪聲的Moore響度模型,從譜質心特征的數學定義推導研究譜質心帶寬、譜質心斜度和譜質心峰度的計算公式和物理含義,從而得到艦船輻射噪聲的音色特征模型,并將艦船輻射噪聲的響度和音色特征模型相結合,應用到實際水下目標識別中．

1 艦船輻射噪聲的Moore響度特征模型

響度是描述人耳對聲音感覺強度的心理聲學量,Moore根據人耳的聽覺原理和聲波在人耳中的衰減特性,提出更加接近人耳聽覺特性的響度計算模型.下面介紹Moore響度[6-8]計算過程．首先對聲音信號進行離散傅里葉變換,以1 Hz頻率分辨率將聲音信號的頻率成分進行劃分,聲音信號就看作是以1 Hz為間隔、幅值不變的正弦聲音信號的合成．在信號處理時,采樣頻率高于聲音信號最高分析頻率2倍以上,采樣點數最好與采樣率相同,這樣可使信號的能量集中在原有的頻率上不出現泄漏．聲音信號在傳播過程中通過外耳、中耳時,能量會發生變化,這種變化在具體的響度計算模型中用外耳和中耳的傳遞函數表示,本文采用三次多項式函數進行插值得到傳遞函數．

首先將經外耳和中耳后的聲音信號轉換成激勵模型,激勵級表示的是聲音信號經過外耳和中耳后在耳蝸中的聲音能量級,根據下式轉換為激勵級LERB-level:

(1)

式中,ERB帶寬Ewidth=24.673(4.368f/1000+1);p0=2×10-5Pa為參考聲壓;指數權函數w(gk)=(1+pkgk)exp(-pkgk),gk=(fk-f)/f,pk=4f/Ewidth,fk表示有效頻率成分的頻率值．

聲音信號經過耳蝸后到達基底膜,用372個濾波器來模擬基底膜上的響應,即進行特性響度的計算．人耳的聽覺頻率范圍是50～1.5×104Hz,由Enumber=21.366log(4.368Fi/1000+1)換算得到聽覺頻率范圍是1.8～38.9 ERB，其中Enumber為ERB數，Fi為濾波器的中心頻率.以0.1 ERB為間隔,得到372個濾波器,聲音信號通過372個濾波器后的輸出激勵Ei為

(2)

式中,i=1,2,…,372;j為聲音信號的有效頻率數.濾波器采用前面的指數權函數.形式如下所示:

(3)

(4)

根據輸出激勵計算特性響度,即

(5)

式中,ET為可聽閾的能量;G的取值為500Hz以上的ET與500Hz以下的ET的比值;α的取值取決于G的取值;C=0.046871．圖1為上述參數值的示意圖．

圖1 ET,G值和α值的示意圖

根據以上計算步驟,可以得到372個特性響度值,總響度就等于這些特性響度之和,即

(6)

根據上述Moore響度的計算方法,可看出響度是聲音信號幅度和頻率的函數,與幅度變化有很大關系．在心理聲學特征中,相同響度情況下,通過音色可以很好地區分信號.在聲納員聽音判型中,響度和音色是緊密聯系的,下面從音色特征研究艦船輻射噪聲的音色模型．

2 艦船輻射噪聲的音色模型

在聲音響度相同的情況下,音色特征能有效地區分聲音信號．螺旋槳的槳拍聲以輕重變化為主要特點,音色就是在這種輕重拍的發生、發展、衰變到二者交替輪換中展現出來的動態特性[1]．每種樂器都有其固有的頻率范圍,產生基頻和基頻諧音,帶來不同的音色,而槳拍聲是不同結構的螺旋槳擊水的聲音．不同的船或不同的工況,比如槳的尺寸、槳軸功率、轉速等不同,螺旋槳擊水時具有不同的諧振頻率,相應產生的基音和諧音不同,從而產生音色差別．在樂音中,譜質心是描述聲音信號的頻率分布和能量分布的信息．當聲音集中在高頻時,聲音明亮、清晰、有光澤,相反在低頻,聲音暗、悶、不美[1]．譜質心的物理含義是聲音能量集中的區域,在頻率分析范圍內,將譜能量函數看成是頻率的概率密度函數,譜質心便是頻率的一階矩,基于一維的譜質心不能區分目標,因此提出了動態頻帶的多維譜質心特征提取方法[9].本文在譜質心的基礎上研究二階、三階和四階中心矩,即譜質心帶寬、譜質心斜度和譜質心峰度,并推廣到分段頻段的譜質心、譜質心帶寬、譜質心斜度和譜質心峰度,從而研究艦船輻射噪聲的音色特征模型．

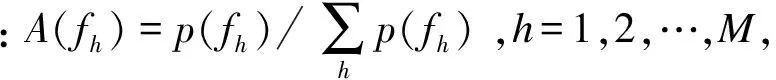
(7)

(8)

(9)

為更好地理解其物理含義,用3個不同頻率、不同聲壓級的正弦信號的合成聲音進行說明:① 60dB、500Hz和60dB、1000Hz的正弦信號合成聲音;② 60dB、500Hz和60dB、800Hz的正弦信號合成聲音;③ 60dB、500Hz和63dB、1000Hz的正弦信號合成聲音．由式(7)～(9)求得3個正弦合成聲音的一維譜質心分別是750,650和833Hz,一維譜質心帶寬分別為250,150和222.5Hz,一維譜質心斜度分別為0, 0和2820.6,一維譜質心峰度分別為62497,22497和91413．譜質心反映信號能量集中的頻率區域,由上述正弦合成聲音,可知譜質心與聲音信號的基頻有很大關系：當分音的幅度不變時,隨著頻率的下降譜質心有所下降；當分音頻率不變時,譜質心靠近幅度最大的分音對應的頻率值．譜質心帶寬是能量分布概率的方差,反映信號能量集中的頻率成分所占的帶寬,譜質心帶寬受聲音信號的頻率和幅度共同影響：當分音的幅度不變時,隨著分音頻率下降譜質心帶寬相應有所下降；當分音的頻率不變、幅度發生變化時,譜質心帶寬要小于幅度變化前的譜質心帶寬．譜質心斜度的值為零時,其能量概率密度函數是對稱分布的．譜質心峰度反映信號能量分布偏離對稱分布的歪斜程度,越接近對稱分布,其值越接近零．

3 仿真驗證

艦船輻射噪聲時變功率譜的簡化模型如下[10]:

G(t,w)=[1+m(t)]Gx(w)+Gl(w)

(10)

其中SL=112+50log(v/10)+15log(DT),航速v為10kn,噸位DT為10kt．Gl(w)是線譜,線譜時域信號仿真模型為

其中，Ak高出連續譜10～25dB；fk=mns,m為諧波次數,n為葉片數,s為轉速(r/s)．

上述艦船輻射噪聲的時變功率譜的采樣頻率為22.5kHz,n為4.由于人耳對聲音響度的分辨率為0.01s,每一幀取為0.01s,觀測1s內的歸一化功率.根據上述的Moore響度計算方法計算Moore響度,并觀測1s內的歸一化Moore響度變化,4種模式的歸一化功率和響度見圖2.

對海上實際數據進行仿真,采樣頻率為22.5kHz,每一幀取為0.01s,經過大量的數據統計,發現0.6s內3類目標A,B,C的Moore響度變化如圖3所示．

由圖2可看出響度主要由功率譜密度的幅度決定,即主要受m(t)的影響,因此艦船輻射噪聲的響度隨著時間的變化而出現緩慢變化的周期效應.將艦船輻射噪聲按照0.01s進行分幀,并對分幀的Moore響度值進行平均,最后將Moore響度均值作為響度特征．

圖2 均勻模式和非均勻模式的歸一化功率和響度變化圖

圖3 3類目標分幀Moore響度變化曲線

針對海上實際數據,截取1s內的數據作為樣本信號,分別得到3類目標基于六分段頻帶的譜質心、譜質心帶寬、譜質心斜度和譜質心峰度的分布圖,如圖4所示．從圖中可看出,六分段的譜質心、譜質心帶寬、譜質心斜度和譜質心峰度有一定的區分度．

將Moore響度的均值作為一維特征,順序排列六分段頻帶的譜質心、譜質心帶寬、譜質心斜度和譜質心峰度值,一共組成25維特征．依據一定的樣本,統計3類目標A,B,C的25維特征,并計算特征的均值和方差,如圖5所示．從圖中可看出,3類目標的均值差異大,方差較小,特征集中度較好,證明組合的25維特征是較為穩健的．

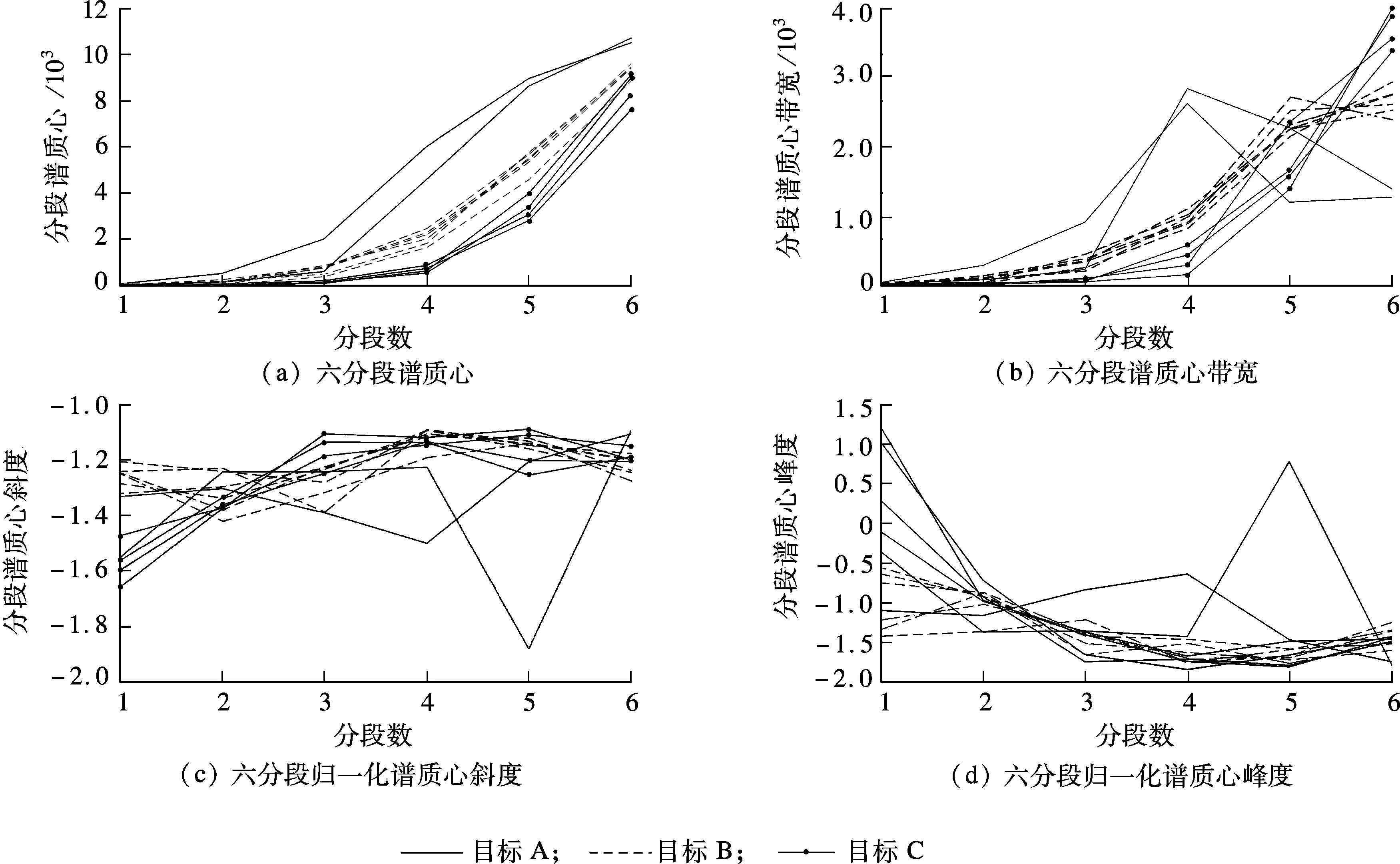
圖4 3類目標的六分段譜質心、譜質心帶寬、譜質心斜度和譜質心峰度分布圖

圖5 3類目標25維特征的均值和方差分布圖

提取3類目標的響度和音色一共25維特征作為目標分類的識別特征,對130個樣本進行試驗,驗證特征提取方法的有效性．分類器采用BP神經網絡分類器,結構層數為3層,隱含層的層數為10,采用批處理方法,試驗結果如表1所示．從表1可看出,將Moore響度和音色一共25維特征作為識別特征,其目標識別率較高,表明提取目標的響度和音色特征矢量作為識別特征對目標進行分類是有效的．

表1 3類目標的識別率

4 結語

聲納員聽音判型是一種有效的目標識別方法,建立相應的數學模型是研究難點．本文基于艦船輻射噪聲的仿真模型研究Moore響度的變化規律,將Mooer響度均值作為一維特征,并在譜質心數學定義的基礎上推導譜質心帶寬、譜質心斜度和譜質心峰度的公式．由于一維的譜質心很難區分目標,因此提出基于分段頻帶的譜質心、譜質心帶寬、譜質心斜度和譜質心峰度的音色特征模型．分析基于Moore響度和音色特征模型相結合的特征的均值和方差,得出這25維特征具有一定的穩健性,進一步將其應用于目標識別中,實驗結果表明這一特征提取方法是有效的．實際中,鑒于目標聲學特性的復雜多變性,本方法的穩健性還有待進一步研究．

)

[1]劉載芳, 王大訓, 張友奎. 聲納聽音判型 [M]. 北京: 海軍出版社,1999.

[2]Park T H. Automatic musical instrument recognition [D]. Tampere, Finland: Tampere University of Technology, 2001.

[3]Giulio A, Maurizio L, Emanuele P. Musical instrument timbres classification with spectral features [J].JournalonAdvanceinSignalProcessing, 2003,2003(1): 5-14.

[4]Xin Z, Zbigniew W. Analysis of sound features for musical timbre recognition [C]//InternationalConferenceonMultimediaandUbiquitousEngineering. Seoul,Korea, 2007: 26-28.

[5]王娜, 陳可安. 水下噪聲音色屬性回歸模型以及在目標識別中的應用[J]. 物理學報, 2010, 59(4): 2873-2881.

Wang Na, Chen Ke’an. Regression model of timbre attribute for underwater noise and its application to target recognition [J].ActaPhysicaSinica, 2010,59(4): 2873-2881. (in Chinese)

[6]Zwicker E, Fastl H.Psychoacoustics:factsandmodels[M]. 2nd ed. Berlin: Spring-Verlag, 1999: 204-237.

[7]Moore B C J, Glasberg B R,Baer T. A model for the prediction of thresholds, loudness, and partial loudness [J].AcousticalSocietyofAmerica, 1997,45(4): 224-239.

[8]Moore B C J. ANSE S3.4-2005 Procedure for the computation of loudness of steady sounds [S]. New York: American National Standards Institute, 2005.

[9]王娜, 陳克安. 分段譜質心特征在水下目標識別中的應用[J]. 兵工學報, 2009, 30(2): 144-149.

Wang Na, Chen Ke’an. Application of sub-band spectral centroid features to recognition underwater targets [J].ActaArmamentarii, 2009,30(2): 144-149. (in Chinese)

[10]錢曉南. 艦船螺旋槳噪聲 [M]. 上海:上海交通大學出版社, 2011.