基于蒙托卡洛仿真的隨機需求庫存優化問題研究

孔繁利，吉日木圖

（內蒙古民族大學a.經濟管理學院；b.數學學院，內蒙古通遼 028043）

0 引言

隨著實際問題的需要，庫存的優化理論逐漸被深入研究，從單級庫存到多級庫存、從單產品庫存到多產品庫存、從確定需求到不確定需求都取得了較好的成果[1-3]。Teimoury等則研究了具有兩類顧客的多產品生產-庫存系統[4]。Consular等研究了允許缺貨和延期交貨下的庫存模型[5]。Abad等研究了在允許部分延期交貨情況下，價格和訂貨量都作為決策變量的一類庫存問題[6]。而影響庫存的主要因素是需求的隨機性，由于需求的規律難以掌握，因此隨機需求條件下的庫存管理問題仍然是供應鏈管理中的一個難點。

本文研究了需求隨機變化條件下的庫存優化問題。在需求變化的情況下，建立了隨機庫存優化模型。并采用蒙特卡洛仿真和Matlab優化技術對建立的庫存模型求解，統計銷售周期和訂貨量出現的頻率，選取出現頻率最大的銷售周期和相應的訂貨量作為最優銷售周期和訂貨量。

1 問題描述

從圖1可以看出在不同的周期內需求對庫存的影響。在第一個周期內需求與供給恰好平衡，在第二周期內需求大于供給，導致存在著不能滿足需求的情況，導致缺貨損失。第三周期內供給大于需求，產生了持貨成本。在這種隨機需求的情況下，本文在滿足一定服務水平下，建立以利潤最大為目標的規劃模型。通過蒙特卡洛仿真和Matlab尋優研究了隨機需求的最優定貨策略。而在需求變化的情況下，由于需求為隨機變量，我們無法求得周期（即兩次訂貨時間間隔）的確切時間，也無法求得再次訂貨點確切來到的時間。最優庫存決策是利用庫存管理方法和庫存控制模型，在滿足需求的情況下，決定存儲點應保持多少庫存、什么時候定貨、訂購量為多少等等以達到庫存總費用最省的目的。

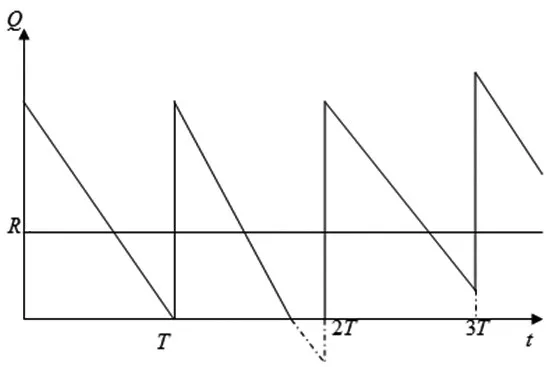
圖1 隨機需求情況的庫存Q（t）的變化情況

2 模型建立

2.1 模型參數

（1）決策變量：TAC為全年總利潤；Q為每次訂貨量；T為銷售周期；

（2）常量：U1為買入單位產品的價格；U2為賣出單位產品的價格；U3為單位缺貨損失；Q1為每周期需求量，Qi為第i天的需求量，此常量受到需求的影響；T′為缺貨周期內的銷售天數；CR為每次的訂貨成本；CH為單位產品的庫存持有成本；MQ,MT分別為每周期最大需求量，周期內最大可能天數。E(β)為在訂貨周期內大于訂貨量的平均需求。β為服務水平。

2.2 模型假設

（1）需求不確定且具有一定量的統計數據；

（2）允許缺貨，缺貨會造成缺貨損失，缺貨預售而不是丟失銷售機會，但需要滿足一定的服務水平。

2.3 模型建立

3 數值算例

由于每天需求量Qi和周期內的需求量Q1需要根據歷史數據計算，因此本文通過蒙特卡洛仿真計算Qi和Q1。

3.1 蒙特卡洛仿真

蒙特卡洛仿真是以概率和統計的理論、方法為基礎的一種計算方法，將所要求解的問題同一定的概率模型相聯系，用計算機實現統計模擬及抽樣，從而獲得問題的近似解[5]。其基本思想是：首先為處理的問題建立一個概率模型，然后產生該問題的統計抽樣樣本，最后分析樣本的特征，并以此作為原問題的解。其主要的理論依據是概率與數理統計中的大數定律。采用蒙特卡洛仿真時，需要做大量的統計模擬才能獲得原問題的近似解，因此計算量非常大[1]。本文求解上述隨機需求的優化模型（5）蒙特卡洛仿真步驟如下：

（1）根據每天需求量的分布，統計其概率分布并進行隨機編碼；

（2）根據隨機編碼產生隨機數，計算模型（2.5）中的統計量Qi,Q1，其中Q1是Qi的和；

（3）對于任意的銷售周期T∈[0,MT]和訂貨量Q∈[0,MQ]和相應的隨機統計量Qi,Q1，利用Matlab優化技術計算TAC并求解最優的TAC和相應的訂貨量和銷售周期；

（4）重復計算步驟二和步驟三N次，獲得N次最優值TAC和相應訂貨量和銷售周期；

（5）統計訂貨量和訂貨周期的概率分布，以出現頻率最高的定貨量和銷售周期作為最優的訂貨量和銷售周期。

3.2 實際算例

本文以某種飲料作為研究對象。其中買入單位產品的價格U1=80（元/箱）；賣出單位產品的價格U2=100（元/箱）；單位缺貨損失U3=15（元/箱）；每次的訂貨成本CR=300（元）；單位產品的存儲費用CH=0.2（元/箱）；每周期最大需求量，周期內最大可能天數分別為MQ=200,TQ=100。零售商統計1000天此飲料的每天需求量（單位：箱/天）分布，如表1：

表1 1000天的產品每天需求量的分布 （單位：需求量，箱/天）

（1）對每天需求量進行隨機編碼。根據每天的需求量，計算頻率和累計頻率。根據累計頻率進行隨機編碼，如表2。

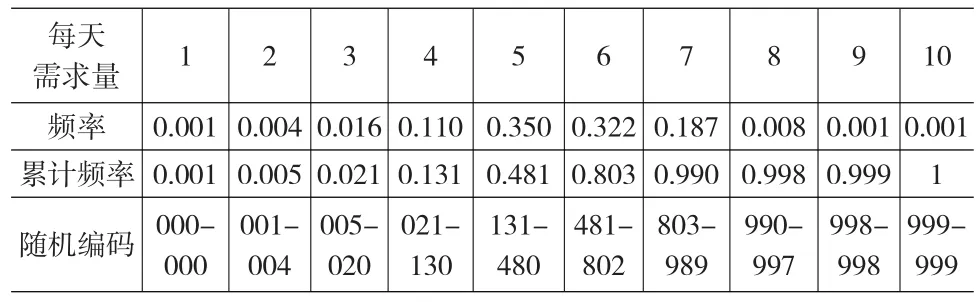
表2 產品的每天需求量的概率分布及隨機編碼

（2）在服務水平β=0.95,β=0.80兩種情況下，根據蒙特卡洛的仿真步驟2、3、4對模型（5）求N=1000次最優解，在服務水平為0.95時，將模擬1000次的最優訂貨批量與銷售周期及其頻數、頻率統計和匯總，見表3、表4：

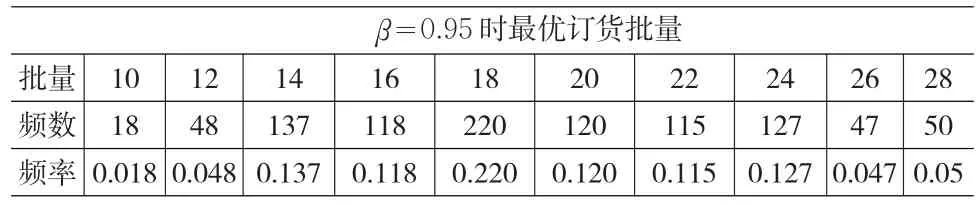
表3 服務水平為0.95時最優訂貨批量

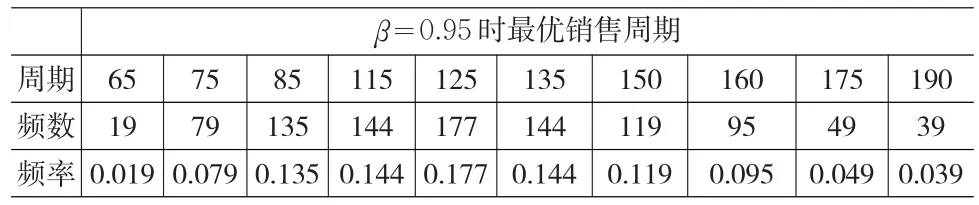
表4 服務水平為0.95時最優訂貨周期

模擬1000次，數值運算結果在不同周期的訂貨量情況和銷售周期統計頻數情況見圖2-圖3。

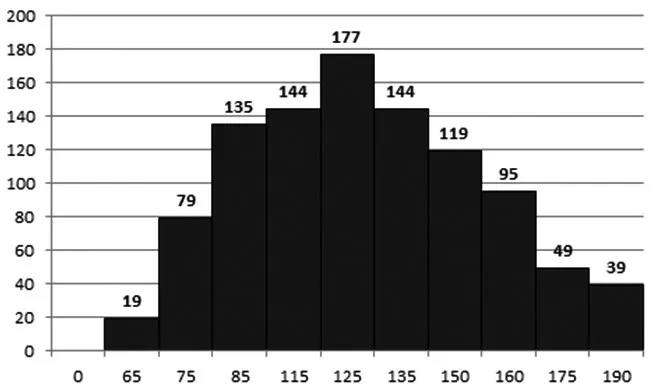
圖2 服務水平β=0.95下的最優訂貨批量分布圖

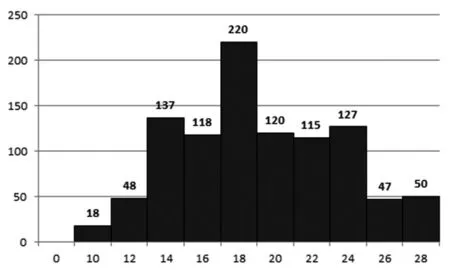
圖3 服務水平β=0.95下的銷售周期分布圖

而在服務水平為0.80時，將模擬1000次的最優訂貨批量與銷售周期及其頻數、頻率統計和匯總，見表5、表6：

表5 服務水平為0.80時最優訂貨批量

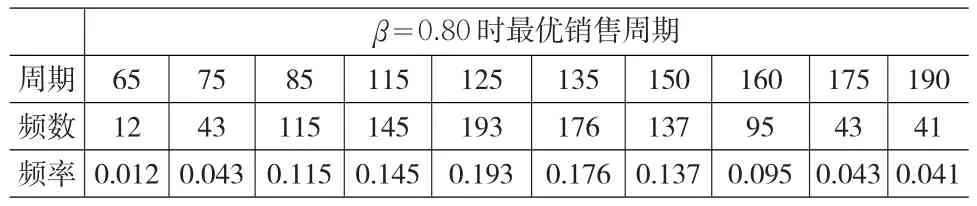
表6 服務水平為0.80時最優訂貨周期

模擬1000次，數值運算結果在不同周期的訂貨量情況和銷售周期統計頻數情況見圖4-圖5。

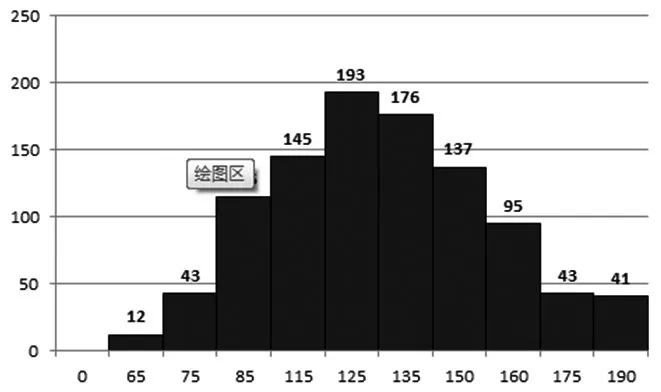
圖4 服務水平β=0.80下的最優訂貨批量分布圖

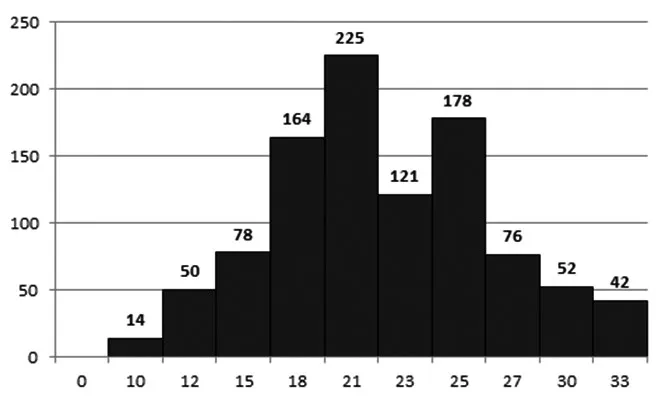
圖5 服務水平β=0.80下的銷售周期分布圖

根據數據的統計結果與訂貨量和銷售周期分布圖2-圖5，在β=0.95下，我們可以看出數據銷售周期18-25天占有總量得50%以上，其中銷售量為21所占有的比例最大，而銷售量在120-140箱在銷售量中占有50%以上。為了科學客觀地反映最優訂貨批量和銷售周期，本文采用訂貨批量期望和銷售周期期望，如下：

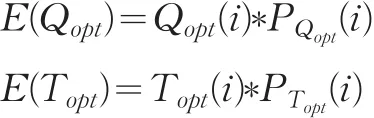
其中E(Qopt)和E(Topt)分別為模擬1000次后確定的最優訂貨批量和銷售周期的期望值；Qopt(i)和Topt(i)分別為第i個最優訂貨批量和銷售周期結果；PQopt(i)和PTopt(i)分別為1000次模擬中第i個最優訂貨批量和銷售周期對應的發生頻率。計算結果如表7：

表7 不同服務水平下的最優銷售周期及批量期望

因此，在β=0.95時，最優銷售周期選取為Topt=19天，對應的訂貨量為Qopt=126箱。因此在β=0.80時，最優的銷售周期為Topt=22天，相應的訂貨量為Qopt=131箱。

4 結論

本文采用蒙特卡洛仿真求解隨機庫存問題，獲得了統計上的最優訂貨量和銷售周期。為隨機需求，但掌握市場需求動態的管理者提供了一種決策方法。但是本文仍然需要有進一步研究的內容，例如，對多產品隨機需求下的庫存問題。隨機需求下多級庫存問題（牛鞭效應增加了問題的復雜性）等都需要進一步分析。

[1]汪傳旭，蔣良奎.模糊隨機需求條件下供應鏈定期庫存訂貨策略研究[J].山東大學學報(理學版)，2011,(7).

[2]Landinnr,Mendeslts,Vazlpr.Combined Effects of Tidal and Rotational Distortions on the Equilibrium Configuration of Low-Mass,Pre-Main Sequence Stars[J].A＆A，2009，494.

[3]Porteus,E.L.Foundations of Stochastic Inventory Control,Stanford [M].CA:Stanford University Press,2002.

[4]Teimoury E,Etal.Aqueueing Approach to Product Io-Inventory Planning for Supply Chain with Uncertain Demands:Case St Udy o f PAKSHOO Hemicals Company[J].Journal of Manufacturing Systems,2010, 29(1).

[5]Consular KV,De Kok T,Rutten W.Two Replenishment Strategies for the Lost Sales Inventory Model:a Comparison[J].International Journal of Production Economics,1996,46～47.

[6]Abad P L.Optimal Price and Order Size for a Reseller under Partial Backordering[J].Computers and Operations Research,2001,28.