圓筒型無鐵心永磁直線電機(jī)空載磁場(chǎng)解析計(jì)算

董劍寧 陳艷龍 黃允凱 金 龍

(東南大學(xué)電氣工程學(xué)院，南京210096)

直線電機(jī)無需借助機(jī)械齒輪、滾珠絲杠等轉(zhuǎn)換裝置即可實(shí)現(xiàn)直線運(yùn)動(dòng)，具有結(jié)構(gòu)簡(jiǎn)單、動(dòng)態(tài)性能好等優(yōu)點(diǎn)，近年來在交通運(yùn)輸、伺服控制、建筑工程、醫(yī)療器械等領(lǐng)域獲得越來越廣泛的應(yīng)用.

高精度伺服應(yīng)用要求永磁直線電機(jī)具有盡可能低的定位力矩和單邊力矩.因此，采用無槽動(dòng)子的圓筒形永磁直線電機(jī)成為此類應(yīng)用的首選.這種電機(jī)定子永磁體分為表貼式和內(nèi)嵌式2 種:前者沿徑向充磁，貼裝在磁軛的表面;后者沿軸向充磁，嵌在鐵心之間［1－2］.為進(jìn)一步降低動(dòng)子慣量以提高電機(jī)加速能力，可采用無鐵心動(dòng)子結(jié)構(gòu)［3］.此時(shí)，為增強(qiáng)主磁場(chǎng)，定子一般采用Halbach 陣列結(jié)構(gòu)或內(nèi)嵌式的聚磁結(jié)構(gòu)［4］.

文獻(xiàn)［5］提出一種定、動(dòng)子均無鐵心的圓筒型無鐵心永磁直線電機(jī)結(jié)構(gòu).其定子由軸向充磁的圓柱型永磁體組成，相鄰永磁體充磁方向相反，且緊貼在一起，中間無鐵磁性極靴.與普通的定子無鐵心圓筒型直線電機(jī)相比，該電機(jī)對(duì)永磁磁通的利用率更高，對(duì)動(dòng)子偏心的敏感度更低，運(yùn)動(dòng)過程中繞組電感變化更小，因而具有更高的效率和控制精度［6］.目前，這種結(jié)構(gòu)的圓筒型無鐵心永磁直線電機(jī)已在納米級(jí)高精度伺服系統(tǒng)中獲得應(yīng)用［7］，但國內(nèi)外關(guān)于此種電機(jī)電磁場(chǎng)分析的文獻(xiàn)較少.

為準(zhǔn)確分析直線電機(jī)的電磁場(chǎng)分布，優(yōu)化電機(jī)設(shè)計(jì)，國內(nèi)外學(xué)者提出了多種方法.其中最常用的是等效磁路法［8］，該方法簡(jiǎn)單易用，但存在模型不準(zhǔn)確的問題，在漏磁較大或磁路復(fù)雜時(shí)尤為嚴(yán)重.采用有限元法［9］可以對(duì)復(fù)雜邊界、多種媒介以及非線性、飽和等問題進(jìn)行有效處理，具有明顯的優(yōu)越性，但前處理和計(jì)算耗時(shí)較長(zhǎng)，不適合在電機(jī)優(yōu)化設(shè)計(jì)的迭代計(jì)算中使用，一般用于確定各項(xiàng)尺寸參數(shù)后的電磁性能核算.使用解析法計(jì)算電磁場(chǎng)可以克服上述2 種方法的缺點(diǎn)，其特點(diǎn)是計(jì)算時(shí)間短，且不需要復(fù)雜的前處理，能直觀地表述各項(xiàng)參數(shù)對(duì)磁場(chǎng)分布的影響，以便調(diào)整參數(shù)進(jìn)行優(yōu)化設(shè)計(jì).但解析法不能考慮鐵心磁導(dǎo)率的非線性，僅適用于磁路飽和程度低的場(chǎng)合.文獻(xiàn)［1，10－11］均為解析法在直線電機(jī)電磁設(shè)計(jì)中的典型應(yīng)用.

本文所研究的圓筒型無鐵心永磁直線電機(jī)定、動(dòng)子上均無鐵心，磁路線性且具有高度對(duì)稱性，非常適合解析法的應(yīng)用.本文首先在圓柱坐標(biāo)系下采用磁荷模型計(jì)算出單個(gè)圓柱形永磁體的磁場(chǎng)分布，再應(yīng)用疊加原理得到整個(gè)電機(jī)的氣隙磁場(chǎng)分布.之后在空載磁場(chǎng)的基礎(chǔ)上推導(dǎo)出電機(jī)反電勢(shì)和推力表達(dá)式.最后通過有限元軟件對(duì)解析計(jì)算結(jié)果進(jìn)行驗(yàn)證，證明了該解析法的正確性.

1 磁場(chǎng)計(jì)算

1.1 磁荷模型

在無電流的永磁體和空氣區(qū)域，磁感應(yīng)強(qiáng)度矢量B 和磁場(chǎng)強(qiáng)度矢量H 滿足下式:

根據(jù)矢量場(chǎng)的亥姆霍茲定理，存在標(biāo)量φm，使

再將永磁體本構(gòu)關(guān)系B =μ0(H +M)代入式(1)、(2)可得

式中，M 為永磁體的磁化矢量.對(duì)式(3)中的拉普拉斯算子應(yīng)用格林函數(shù)，可解得

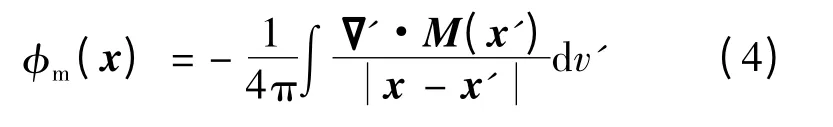
式中，x 為場(chǎng)點(diǎn)的位置矢量;x′為源點(diǎn)的位置矢量.M 僅存在于永磁區(qū)域內(nèi)，因在永磁區(qū)域表面M 突變?yōu)?，式(4)需寫為

式中，v′為永磁區(qū)域;s′為v′的表面;n 為s′外法方向上的單位矢量.參考電荷模型，可假設(shè)在永磁體內(nèi)存在體密度ρm=－▽·M，表面密度σm=M·n的磁荷.由此可推得，空氣中x 處的磁密為［12］

1.2 空載磁場(chǎng)求解

對(duì)于組成圖1中圓筒型無鐵心永磁直線電機(jī)定子的某個(gè)軸向充磁的圓柱形永磁體(見圖2)而言，僅左右兩個(gè)圓形底面上存在密度為M 的磁荷.僅考慮右底面上的磁荷，由其引起的φm為的坐標(biāo)，ρ，φ 為場(chǎng)區(qū)點(diǎn)的坐標(biāo).對(duì)使用文獻(xiàn)［13］中的積分變換，可得

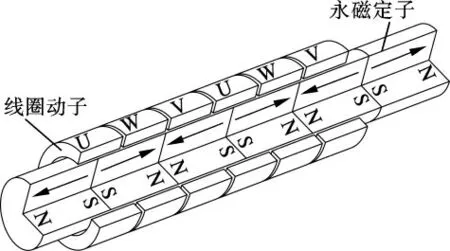
圖1 圓筒型無鐵心永磁直線電機(jī)結(jié)構(gòu)

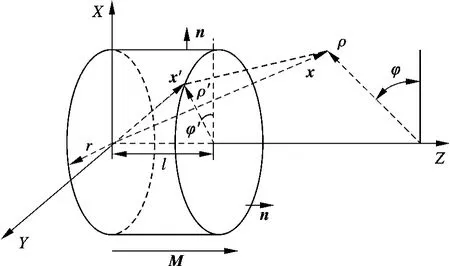
圖2 單個(gè)軸向充磁的圓柱形永磁體模型

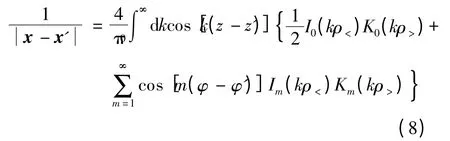
式中，Im，Km分別為第一類和第二類m 階虛宗量的貝塞爾函數(shù);ρ＞(ρ＜)為ρ 和ρ′中的較大(小)者.由磁場(chǎng)的軸對(duì)稱性知，φm1與φ 無關(guān)，為簡(jiǎn)化計(jì)算，可令φ=0.將式(8)代入式(7)，有

式中，l 為圓柱形永磁體的長(zhǎng)度.由于其中二重積分的第2 項(xiàng)為0，式(9)可簡(jiǎn)化為

利用虛宗量的貝塞爾函數(shù)的性質(zhì)［14］，對(duì)式(10)中的第2 個(gè)積分進(jìn)行處理，可得在ρ ＞r 的區(qū)域(即空氣)內(nèi)，有

對(duì)其求梯度，可得到空氣中磁通密度的徑向和軸向分量分別為

同樣可求出由永磁體的左底面上的磁荷引起的磁密分量為

由于磁路線性，可直接利用疊加原理，得到由n 個(gè)永磁體組成的圓筒型無鐵心永磁直線電機(jī)定子的空載磁密為

2 反電勢(shì)與推力計(jì)算

圓筒型無鐵心永磁直線電機(jī)的動(dòng)子繞組線圈軸對(duì)稱地環(huán)繞在定子外，每相繞組由若干組線圈串/并聯(lián)而成.圖3為動(dòng)子繞組示意圖，其中Rco為線圈的外半徑，Rci為其內(nèi)半徑，wc為每組線圈寬度.

圖3 動(dòng)子繞組示意圖

根據(jù)法拉第電磁感應(yīng)定律，動(dòng)子沿Z 軸作直線運(yùn)動(dòng)時(shí)，每根環(huán)形線圈內(nèi)都會(huì)切割徑向磁場(chǎng)感應(yīng)出反電勢(shì).根據(jù)空載磁場(chǎng)計(jì)算結(jié)果推導(dǎo)出每根線圈內(nèi)產(chǎn)生的反電勢(shì)，再將同相線圈的反電勢(shì)相加即可得到相反電勢(shì).但這樣計(jì)算過程復(fù)雜，耗時(shí)長(zhǎng).為簡(jiǎn)化計(jì)算，可假設(shè)所有線圈均集中在平均半徑處.如圖3所示，設(shè)某組線圈軸線所在位置為z，則該組線圈區(qū)域內(nèi)的徑向磁密平均值為

該組線圈在該位置時(shí)的反電勢(shì)為

式中，v 為動(dòng)子運(yùn)動(dòng)速度;Nc為該組線圈的串聯(lián)匝數(shù);Lav為每匝線圈的平均長(zhǎng)度.將同相的每組線圈中的反電勢(shì)相加，即可得到每相繞組反電勢(shì)波形.

動(dòng)子上的推力是由電樞電流與空載磁場(chǎng)相互作用而產(chǎn)生的洛侖茲力.同樣認(rèn)為線圈集中在平均磁密處，可得一組線圈的推力為

將所有線圈組上的推力相加，即可得到總的動(dòng)子推力.

3 結(jié)果對(duì)比與分析

使用以上解析模型分析了某型號(hào)圓筒型無鐵心永磁直線電機(jī)，計(jì)算了其空載磁場(chǎng)、反電勢(shì)和動(dòng)子推力.該型號(hào)電機(jī)的主要參數(shù)如表1所示.

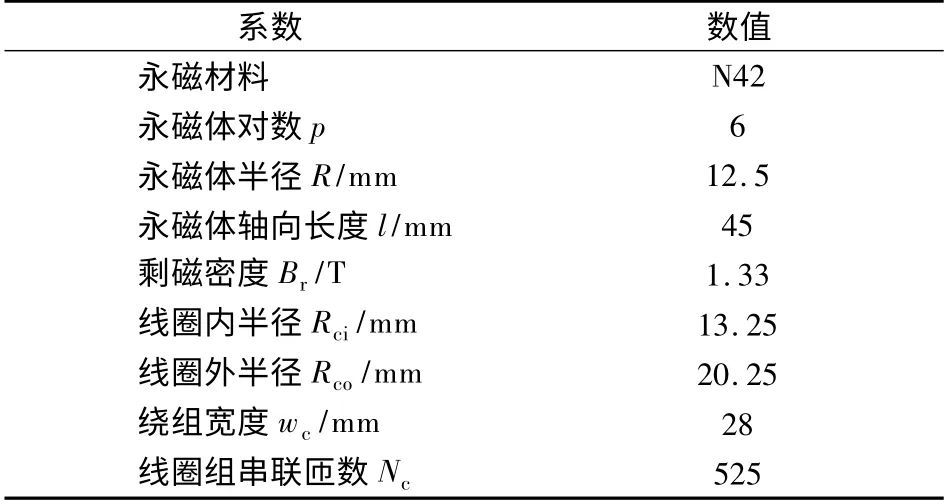
表1 某型號(hào)圓筒形無鐵心永磁直線電機(jī)主要參數(shù)

為驗(yàn)證以上解析計(jì)算方法的正確性，建立了該電機(jī)的二維軸對(duì)稱有限元模型，圖4給出了有限元法計(jì)算出的空載磁場(chǎng)分布結(jié)果.和徑向分量的有限元法和解析法計(jì)算結(jié)果.可看出隨著軸向距離的增加，空載磁密呈周期性變化.受邊端效應(yīng)影響，邊緣處磁密快速下降.解析法相對(duì)于有限元法的最大偏差出現(xiàn)在徑向磁密最大的位置，但此時(shí)誤差也在5%以內(nèi).出現(xiàn)偏差的主要原因是最大磁密處對(duì)應(yīng)的實(shí)際磁化強(qiáng)度要低于解析模型中使用的剩余磁化強(qiáng)度.

圖4 圓筒形無鐵心永磁直線電機(jī)的磁場(chǎng)分布

圖5 ρ=13 mm 處解析法與有限元法磁密計(jì)算結(jié)果對(duì)比

圖6給出了2 種方法計(jì)算出的動(dòng)子以1 m/s速度沿軸向運(yùn)動(dòng)時(shí)U 相繞組中的反電勢(shì)波形，可見2 種計(jì)算方法所得結(jié)果非常接近，最大誤差為7%.二者存在偏差的原因除磁化強(qiáng)度的偏差外還有解析模型中對(duì)線圈所作的平均化處理.

圖6 動(dòng)子運(yùn)動(dòng)速度為1 m/s 時(shí)U 相繞組的反電勢(shì)

在繞組中通入有效值為1.3 A 的三相對(duì)稱電流，并使電流位于q 軸上，得到如圖7所示的動(dòng)子推力曲線.由圖可知，解析法與有限元法計(jì)算出的推力波形接近.解析法所得推力平均值為77.8 N，有限元法結(jié)果為79.0 N，兩者偏差小于2%.

圖7 一個(gè)電周期內(nèi)動(dòng)子受力曲線

圖8對(duì)比了負(fù)載狀態(tài)下，ρ=13 mm 處，A 相線圈電流達(dá)到幅值時(shí)對(duì)應(yīng)極面下的磁密波形以及相同位置的空載磁密波形.2 種波形均由有限元分析得到.由圖可見，2 種波形非常接近，這說明負(fù)載電流對(duì)電機(jī)磁場(chǎng)的影響非常小，這也是該種電機(jī)的優(yōu)點(diǎn)之一.

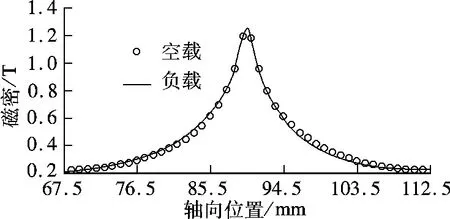
圖8 空載與負(fù)載時(shí)一個(gè)極面下的磁密波形

4 結(jié)語

本文應(yīng)用磁荷法在圓柱坐標(biāo)系下導(dǎo)出了圓筒型無鐵心永磁直線電機(jī)的空載磁場(chǎng)解析計(jì)算模型，給出了空載磁場(chǎng)軸向和徑向分量的解析公式.在此基礎(chǔ)上，對(duì)線圈區(qū)域進(jìn)行平均化處理，求出電機(jī)相反電勢(shì)和推力的解析公式.之后利用此解析方法分析了某型號(hào)圓筒型無鐵心永磁直線電機(jī)，所得結(jié)果與有限元法所得結(jié)果進(jìn)行了對(duì)比，驗(yàn)證了解析法的正確性.本文所提出的解析計(jì)算方法適用于該種電機(jī)的電磁設(shè)計(jì)，對(duì)于其他永磁直線電機(jī)的理論分析也有參考價(jià)值.

References)

［1］趙鏡紅，張曉峰，張俊洪.圓筒永磁直線同步電機(jī)磁場(chǎng)和推力分析［J］.電機(jī)與控制學(xué)報(bào)，2010，14(1):12－17.

Zhao Jinghong，Zhang Xiaofeng，Zhang Junhong.Field and thrust analysis of tubular permanent magnet linear synchronous motor［J］.Electrical Machines and Control，2010，14(1):12－17.(in Chinese)

［2］王詠菲.圓筒型永磁直線同步電機(jī)的電磁場(chǎng)分析與研究［D］.天津:天津大學(xué)電氣與自動(dòng)化工程學(xué)院，2008.

［3］劉曉.空心式永磁直線伺服電機(jī)及其驅(qū)動(dòng)控制系統(tǒng)研究［D］.杭州:浙江大學(xué)電氣工程學(xué)院，2008.

［4］Trumper D，Kim W，Williams M.Design and analysis framework for linear permanent magnet machines［J］.IEEE Transactions on Industry Applications，1996，32(2):371－379.

［5］Ishiyama N.Linear motor equipped with a stator which is easily assembled:US，6040642［P］.2000.

［6］Suzuki A，Yoshida T.Position detection for shaft－type linear motor by measurement of shaft surface magnetic flux［C］//Proceedings of International Conference on Electrical Machines and Systems.Tokyo，Japan，2009:5382917－01－06.

［7］Nippon Pulse Ltd.Linear shaft motor—nippon pulse［EB/OL］.(2011－08－09)［2012－09－06］.http://www.nipponpulse.com.

［8］Mizuno T，Yamada H.Magnetic circuit analysis of a linear synchronous motor with permanent magnets［J］.IEEE Transactions on Magnetics，1992，28(5):3027－3029.

［9］Tomczuk B，Schroder G，Waindok A.Finite－element analysis of magnetic field and electromechanical parameters calculation for a slotted permanent－magnet tubular linear motor［J］.IEEE Transactions on Magnetics，2007，43(7):3229－3236.

［10］Wang J，Howe D，Jewell G.Analysis and design optimization of an improved axially magnetized tubular permanent－magnet machine［J］.IEEE Transactions on Energy Conversion，2004，19(2):289－295.

［11］王淑紅，熊光煜.新型筒型永磁動(dòng)圈式直線電動(dòng)機(jī)氣隙磁場(chǎng)解析分析［J］.電工技術(shù)學(xué)報(bào)，2007，22(5):41－46.

Wang Shuhong，Xiong Guangyu.Analysis of air gap field in a new tubular linear PM motor with moving coil［J］.Transactions of China Electrotechnical Society，2007，22(5):41－46.(in Chinese)

［12］Furlani E.Permanent magnet and electromechanical devices［M］.New York:Academic Press，2001.

［13］胡嗣柱，倪光炯.數(shù)學(xué)物理方法［M］.上海:復(fù)旦大學(xué)出版社，1989.

［14］Olver F，Lozier D，Boisvert R，et al.NIST handbook of mathematical functions［M］.New York:Cambridge University Press，2010.