一種線性/非線性自回歸模型及其在建模和預測中的應用

馬家欣 許飛云 黃 仁

(東南大學機械工程學院，南京211189)

時間序列分析是現代系統辨識的重要方法之一，它在缺乏明確或者完全的系統輸入與輸出因果關系的情況下，將白噪聲看作系統輸入，從數理統計的角度揭示因果關系，最終求得系統的等價模型.該方法在各個領域都得到了廣泛的應用［1-4］.

ARMA 模型(包括AR 模型和MA 模型)是時序方法中最基本的時序模型，然而，它是在線性回歸模型的基礎上引申發展起來的，很難模擬工程實際中的非線性現象.而經典的非線性時間序列模型，包括門限自回歸模型、雙線性模型、指數自回歸模型等，一般都是在特定的工程背景下提出的，通用性不夠.因此亟須提出一種適用于線性/非線性系統的時序模型.GNAR 模型的提出和應用，在形式上統一了不同背景下提出的非線性時序模型的表達式，并有機結合了線性模型［5-7］.另一方面，盡可能地利用更多的已知信息，獲取更多的系統特性，可進一步提高建模精度.因此，在經典時序模型的基礎上，把影響系統輸出的已知相關數據作為系統輸入，可得到帶有外部輸入的時序模型，如ARX，ARMAX 等模型.這些模型不僅在理論上得到了驗證，在工程實際中也得到了廣泛應用［8-11］.本文針對系統輸入部分已知的特點，在GNAR 模型基礎上提出了GNARX 模型，給出了模型的參數估計和結構選取方法，并將該模型應用于仿真和實際數據，效果優于其他模型.

1 GNARX 模型表達式

GNAR 模型建模時，認為系統輸入是零均值的白噪聲.如果系統已知單個輸入，記作序列{ut}，系統的輸出序列記作{wt}，白噪聲記作{at}，那么GNAR 模型就變形為單輸入的GNARX 模型.

對于單輸入系統，設t 時刻輸出值為wt，表示為函數f 的表達式，即

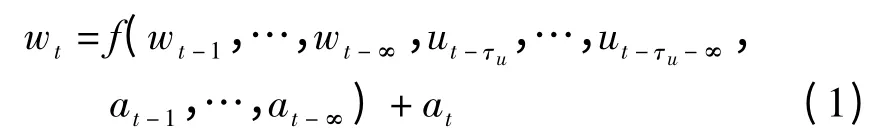
式中，f(·)為任意一般線性/非線性函數;wt－i為t－i 時刻的系統輸出觀測值，i =1，2，…;ut－τu－i為t－τu－i 時刻的系統輸入，i =1，2，…;at－i為t－i 時刻的白噪聲，i=1，2，…;τu為系統輸入ut的延遲.

對于一般線性平穩系統，式(1)中函數f 表示ARMAX 模型;而當系統表現出非線性、非平穩特征時，由Weierstrass 逼近原理［12］知，可用多項式逼近式(1)中的f 函數:

式中，α1，α2，…，β1，β2，…，λ1，λ2，…是模型參數.

假設式(2)描述的系統具有零初始狀態(即wt=0，t≤0)，且系統在初始時刻之前沒有輸入(即ut=0，t≤0).實際建模中，模型階次p 取有限值，令xt，i表示式(2)中的各i 階項，xt，i，1(i=1，2，…，p)表示i 階項xt，i中的1 次項，即

則系統輸出wt可寫成如下形式:

式中，θ(i1)，θ(i1，i2)，…為模型參數;xt，i，1(j)為向量xt，i，1中的第j 個元素;nw，j(j =1，2，…，p)為輸出{wt}各階項的記憶步長;nu，j(j =1，2，…，p)為輸入{ut}各階項的記憶步長.該模型簡記為GNARX(p;τu;nw，1，nw，2，…，nw，p;nu，1，nu，2，…，nu，p).

當系統具有雙輸入{ut}，{vt}時，把式(4)推廣至雙輸入的GNARX 模型，簡記為GNARX(p;

式中，nv，j(j =1，2，…，p)為輸入{vt}各階項的記憶步長;τv為系統輸入{vt}的延遲.

同理，式(6)可推廣到多輸入系統，不再贅述.

2 GNARX 模型的參數估計與結構選取

GNARX 模型的參數估計用最小二乘法很容易求得.以式(4)所示的單輸入GNARX 模型為例，在時刻t，p 階項記作xt，p，是一維向量形式.求取過程中用xt，p，i(i=1，2，…，p)表示p 階項xt，p中的i 次項，也是一維向量，其中xt，p，i(j)是標量，表示向量xt，p，i中的第j 個元素.

式中，mpi=Cinw，p+nw，p+nw，p+i－1(i=1，2，…，p).

令

記

于是，t 時刻到t+k 時刻的方程式寫成

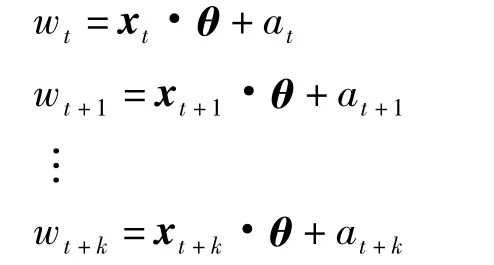
θ 參數最小二乘法估計為

其中

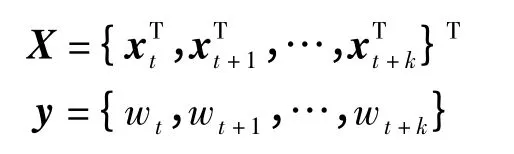
根據式(9)即可對單輸入GNARX 模型進行參數估計.同理，可獲得雙輸入、多輸入模型的參數估計方法.

GNARX 模型結構的辨識，包括模型階次p 的確定和記憶長度的確定，這直接影響著模型的建模性能和預測性能及模型的復雜程度，同時也關系到計算速度、預報實時性等問題.

對于GNARX 模型，定義單輸入模型i 階記憶步長si=nw，i+nu，i(i=1，2，…，p)，雙輸入模型i 階記憶步長si=nw，i+nu，i+nv，i(i =1，2，…，p)，多輸入模型i 階記憶步長可依此類推得到.則i 階參數量ri為

式中，i=1，2，…，p.

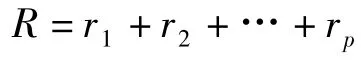
則GNARX 模型參數數量為修正AIC 準則函數［6］如下所示:

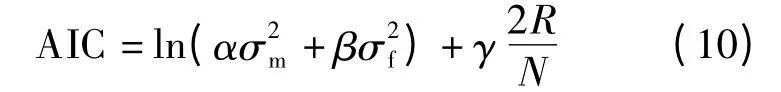
式中，α，β，γ 為重要度權系數;σ2m為建模誤差方差;σ2f為預測誤差方差;N 為數據長度.

式(10)中，建模誤差σ2m的存在，保證了模型的建模能力;引入預測誤差σ2f，可以防止模型的過擬合;而模型參數數量R 的選取則考慮了模型復雜程度對AIC 值的影響，并影響最終模型選取.按信息準則，通常取AIC 值最小處對應的模型為適用模型.

模型結構的最終確定，需要綜合考慮模型的建模能力、預測能力和模型復雜程度等因素.在具體建模過程中，可根據現場要求的不同，調整式(10)中的重要度權系數，來滿足實際建模需求.如模型用于濾波，則可增加建模重要度權系數α;若模型以預報為主，則可以增加預測重要度權系數β;而當現場側重于建模實時性時，則可以增加模型復雜重要度權系數γ.

3 GNARX 模型的建模和預測應用

GNARX 模型適用范圍廣，對線性和非線性數據有著良好的建模預測能力.下文用GNARX 模型對仿真數據和實際數據進行建模和預測，并與其他模型預測效果進行對比.

為比較建模預測效果，定義如下衡量指標:建模均方誤差

預測均方誤差

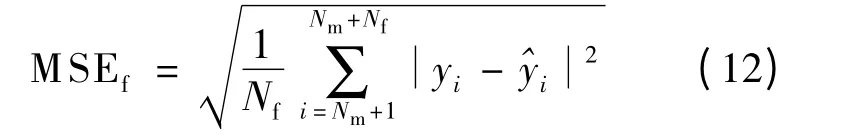
建模平均絕對百分比誤差

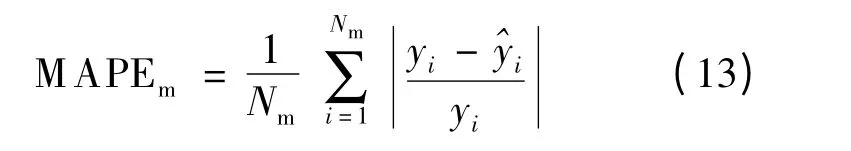
預測平均絕對百分比誤差

式中，yi為模型輸出真值;^為模型輸出估計值;Nm為用于建模的數據長度;Nf為用于預測的數據長度.

3.1 對仿真數據的建模和預測

仿真數據模型具體形式如下:

ARX 模型

ARMAX 模型

NLARX 模型

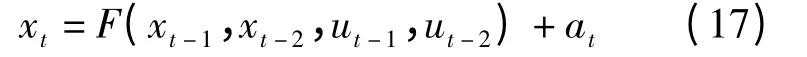
式中，at為白噪聲，服從正態分布N(0，0.1);ut－i(i=1，2，3，…)為系統輸入，服從平均分布U(0，1);xt－i(i=0，1，2，…)為系統輸出;F(·)取Matlab 中S 形網絡非線性估計函數，單元數10，S 形函數表達式為f(z)=1/(1 +exp(－z)).

仿真數據選用前，先對{xt}序列進行歸一化處理，再舍去前50 個過渡區數據，取中間250 個數據用于建模，后100 個數據用于預測.分別用AR 模型、GNAR 模型、ARX 模型、BP 網絡和GNARX 模型對上述各仿真數據進行建模預測.其中時序模型是在合適的模型結構選取范圍內選取的，并用式(10)所示修正AIC 判斷，重要度權系數嘗試選取α=1，β=1，γ=1，模型具體選取范圍見表1.

表1 針對不同數據建模時各模型結構的選取范圍

1)僅以建模預測數據xt作為網絡的輸入，輸入樣本數據重合度記作r，輸入層節點數記作mi，網絡簡記為BP1(mi;mh;mo;r).

2)數據xt，ut同時作為網絡的輸入，xt輸入維數為mx，ut輸入維數為mu，延遲為τu，輸入數據xt的重合度記作r，此時輸入層節點數為mx+mu，網絡簡記為BP2(mx;mu，τu;mh;mo;r).

其中數據重合度針對輸入樣本{xt}而言，設第1 組輸入數據為{xt，xt－1，…，xt－mx}，第2 組輸入數據為{xt－k，xt－k－1，…，xt－k－mx}，把k 記作輸入樣本{xt}的平移量，則數據重合度定義為

網絡訓練時，最大迭代次數設為1.0 ×104，目標誤差為1.0 ×10－3，在一定范圍內改變網絡待定系數(如表中mi，mh和r 等)，最終求取相對較優的網絡模型.

針對上述3 組仿真數據的建模預測，各模型結構選取結果見表2，表中還給出了各模型建模預測的各項誤差指標.通過對比建模預測效果可看出，GNARX 模型建模預測誤差最小，其預測效果見圖1～圖3.

3.2 對振動位移采樣電流數據的建模和預測

振動位移采樣電流數據取自文獻［4］.用GNARX 模型對振動位移采樣電流數據(共150個)建模并預測時，首先對振動位移{x1t}和動態切削力{x2t}分別進行歸一化處理，然后對{x1t}取前120 個數據用于建模，后30 個數據用于預測.因為振動位移與動態切削力存在一定關系，那么對應的采樣電流數據也必然存在某種聯系，所以本文用動態切削力采樣電流數據{x2t}作為GNARX 模型的輸入.各模型選取范圍見表1，模型選取結果及建模預測誤差列于表3中(α =1，β =1，γ =1)，預效果見圖4.

通過分析GNARX 模型應用結果可知:

1)在明確系統輸入的情況下，ARX 和GNARX 模型比AR 和GNAR 模型更為精確，建模預測效果更好.

2)GNARX 模型應用于仿真數據(包括線性和非線性模型數據)，其建模和預測精度明顯高于其他模型，體現了GNARX 模型良好的建模預測能力.

表2 各模型對仿真數據建模預測的誤差對比

圖1 GNARX 模型對ARX 數據的預測效果

圖2 GNARX 模型對ARMAX 數據的預測效果

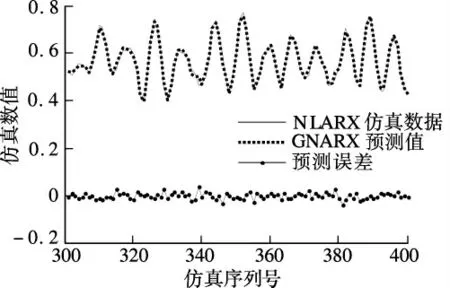
圖3 GNARX 模型對NLARX 數據的預測效果

表3 各模型對振動位移采樣電流建模預測的誤差對比

圖4 GNARX 模型對振動位移采樣電流數據預測效果圖

3)GNARX 模型應用于振動位移采樣電流數據，其建模預測效果同樣優于其他模型，說明GNARX 模型適用于實際數據建模，具有工程應用可行性.

4)GNARX 模型應用于振動位移采樣電流數據的優越性并不明顯，這可能是模型輸入選取不當所造成的，說明動態切削力和振動位移2 組數據間并沒有明顯的輸入輸出關系.

4 結語

將影響系統輸入的相關數據作為外部輸入，在GNAR 模型的基礎上，提出了帶有外部輸入的線性/非線性自回歸模型——GNARX 模型，并給出了其一般表達式及其最小二乘參數估計方法.運用一種綜合考慮建模誤差、預測誤差及模型復雜度的修正AIC 準則，確定GNARX 模型結構，該準則通過改變重要度權系數來適應不同的現場需求，不斷試驗與修改，尋求最優模型.將該模型應用于仿真和實際數據，結果表明，GNARX 模型精度高，通用性好，無論是對ARX，ARMAX，NLARX 等模型的仿真數據，還是對實際工程數據，GNARX 模型都表現出了很好的建模預測能力，效果優于傳統的時序模型及BP 網絡.

由于非線性時間序列的分析與處理要比線性平穩時序復雜得多，且GNARX 模型結構相對冗長，在模型結構的確定、適用性檢驗等方面尚無統一的方法和成熟的理論研究，因此，該模型的理論研究和實際應用都有待進一步探討.

References)

［1］Box G E P，Jenkins G M，Reinsel G C.Time series analysis:forecasting and control［M］.4th ed.Hoboken，USA:John Wiley ＆Sons Inc.，2008.

［2］Flores J J，Graff M，Rodriguez H.Evolutive design of ARMA and ANN models for time series forecasting［J］.Renewable Energy，2012，44:225-230.

［3］Hansen P R，Huang Z，Shek H H.Realized GARCH:a joint model for returns and realized measures of volatility［J］.Journal of Applied Econometrics，2012，27(6):877-906.

［4］楊叔子，吳雅，軒建平.時間序列分析的工程應用:下冊［M］.2 版.武漢:華中科技大學出版社，2007.

［5］陳茹雯，黃仁，張志勝，等.基于數學模型的視覺測量系統圖形畸變校正方法［J］.機械工程學報，2009，45(7):243-248.

Chen Ruwen，Huang Ren，Zhang Zhisheng，et al.Distortion correction method based on mathematic model in machine vision measurement system［J］.Journal of Mechanical Engineering，2009，45(7):243-248.(in Chinese)

［6］Huang Ren，Xu Feiyun，Chen Ruwen.General expression for linear and nonlinear time series models［J］.Frontiers of Mechanical Engineering in China，2009，4(1):15-24.

［7］陳茹雯，黃仁，史金飛，等.線性/非線性時間序列模型一般表達式及其工程應用［J］.東南大學學報:自然科學版，2008，38(6):1077-1080.

Chen Ruwen，Huang Ren，Shi Jinfei，et al.General expression for linear and nonlinear time series model and Its engineering application［J］.Journal of Southeast University:Natural Science Edition，2008，38(6):1077-1080.(in Chinese)

［8］Muhannad Z，Yusoff Z M，Rahiman M H F，et al.Modeling of steam distillation pot with ARX model［C］//IEEE 8th International Colloquium on Signal Processing and Its Applications.Melaka，Malaysia，2012:194-198.

［9］Sanandaji B M，Vincent T L，Wakin M B，et al.Compressive system identification of LTI and LTV ARX models［C］//50th IEEE Conference on Decision and Control and European Control Conference.Orlando，FL，USA，2011:791-798.

［10］Raniman M H F，Taib M N，Salleh Y M.Black box modeling of steam distillation essential oil extraction system using ARMAX structure［C］//International Conference on Intelligent and Advanced Systems.Kuala Lumpur，Malaysia，2007:1059-1062.

［11］Stefanoiu D，Seraficeanu C，Culita J.Identification of MIMO-ARMAX models for glycemia and sodium ions tests through Particle Swarm Optimization［C］//IEEE International Conference on Control and Automation.Christchurch，New Zealand，2009:643-650.

［12］Giardina C R，Chirlian P M.Proof of Weierstrass approximation theorem using band-limited functions［J］.Proceedings of the IEEE，1973，61(4):512.