基于高低頻混合方法的梅利逼近掃頻技術(shù)

馬 驥 龔書(shū)喜 王 興 張鵬飛 呂政良

（西安電子科技大學(xué)天線與微波技術(shù)國(guó)防科技重點(diǎn)實(shí)驗(yàn)室，陜西 西安710071）

引 言

隨著現(xiàn)代電子技術(shù)的發(fā)展，寬頻帶系統(tǒng)的應(yīng)用日益廣泛.在實(shí)際應(yīng)用中，寬帶天線常常安裝在艦船、飛機(jī)以及手機(jī)等移動(dòng)平臺(tái)上.為分析載體平臺(tái)上天線在一定頻率范圍內(nèi)的輻射特性，必須在每個(gè)頻點(diǎn)重復(fù)求解積分方程，這必將耗費(fèi)大量的時(shí)間.因此，如何快速有效得到載體平臺(tái)上天線的寬帶特性具有重要意義.

在電磁計(jì)算中，矩量法（MoM）［1］雖然是一種精確的數(shù)值方法，但受所需內(nèi)存的限制，長(zhǎng)期以來(lái)不能用于電大尺寸問(wèn)題的求解.20世紀(jì)90年代以來(lái)，隨著計(jì)算機(jī)硬件和計(jì)算方法的發(fā)展，計(jì)算電磁學(xué)取得了長(zhǎng)足的進(jìn)步.其中，MoM-PO［2-6］混合方法是研究此類(lèi)問(wèn)題的有效方法.該算法將整個(gè)模型劃分為MoM區(qū)域和物理光學(xué)（PO）區(qū)域，由于MoM-PO方法中只有極少的未知量，因此具有比MoM高得多的計(jì)算效率，并且MoM區(qū)域的電場(chǎng)積分方程考慮了來(lái)自PO區(qū)域的耦合作用，使其計(jì)算精度得到保證.

基于模型估計(jì)［7］、漸近波形估計(jì)［8-9］和梅利逼近［10］等快速掃頻技術(shù)蓬勃發(fā)展.上述方法中，梅利逼近易于與基于積分方程的數(shù)值方法相結(jié)合.本文將其與MoM-PO結(jié)合分析載體平臺(tái)上天線的寬帶特性，通過(guò)坐標(biāo)變換，在給定的頻帶中計(jì)算出切比雪夫節(jié)點(diǎn)，并應(yīng)用MoM-PO計(jì)算出這些節(jié)點(diǎn)處的表面電流，然后通過(guò)梅利逼近快速計(jì)算出該頻帶內(nèi)任意頻點(diǎn)的表面電流，從而實(shí)現(xiàn)寬帶天線的快速掃頻.計(jì)算結(jié)果表明在不失精度的前提下，該方法大大提高了計(jì)算效率.

1 基本理論

1.1 MoM-PO混合算法

考慮含有理想導(dǎo)體載體平臺(tái)和天線的復(fù)雜結(jié)構(gòu)，一般將天線劃分為MoM區(qū)，而將載體平臺(tái)劃分為PO區(qū).在MoM區(qū)應(yīng)用導(dǎo)體目標(biāo)邊界條件可得電場(chǎng)積分方程為

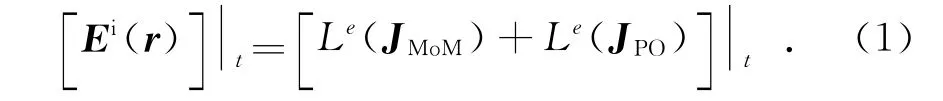
積分算子Le定義為

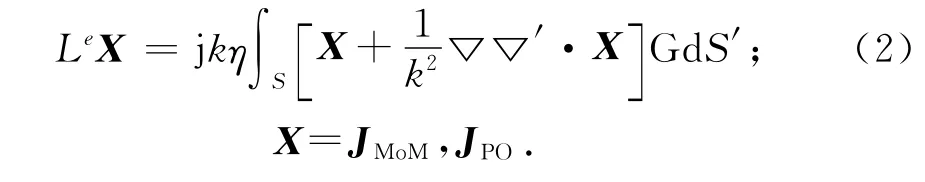
式中：k，η和G分別為自由空間的波數(shù)、波阻抗和格林函數(shù)；JMoM和JPO則分別代表MoM區(qū)和PO區(qū)的感應(yīng)電流，將它們展開(kāi)為

式中：NMoM和NPO分別為MoM區(qū)域和PO區(qū)域未知量數(shù)目；αn和γk分別是MoM區(qū)和PO區(qū)未知電流系數(shù)；fn和fk均為RWG基函數(shù)［11］.

根據(jù)物理光學(xué)逼近，PO區(qū)的感應(yīng)電流可表示為如下形式

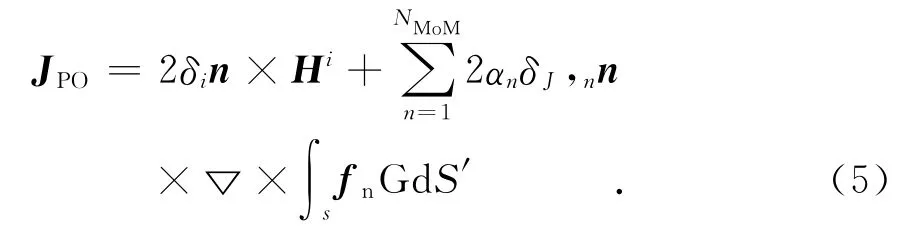
式中：n為PO區(qū)三角面片的單位法向矢量；δi和δJ，n分別代表了入射波（Ei，Hi）和MoM區(qū)基函數(shù)作為源對(duì)場(chǎng)點(diǎn)的遮擋系數(shù)，定義為

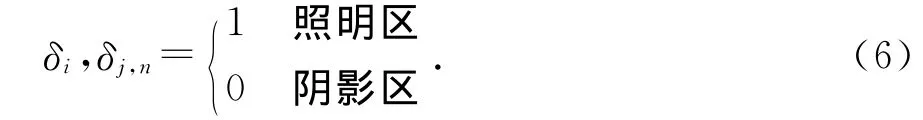
聯(lián)立式（4）和或（5），并在PO區(qū)三角面片的公共邊上引入一對(duì)垂直于該公共邊的單位矢量tk±可得

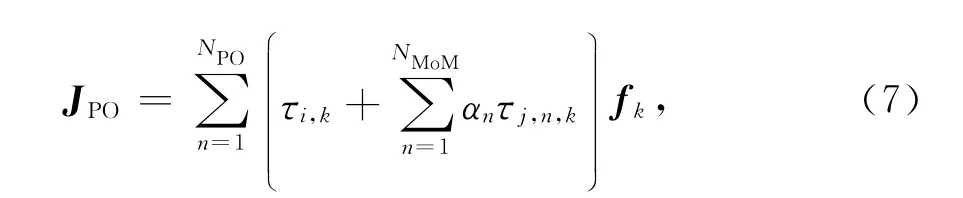
式中：

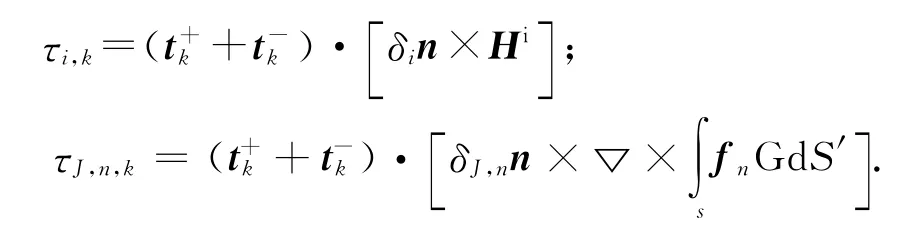
將式（3）和式（7）代入電場(chǎng)積分方程（1）中，并采用伽略金方法，利用測(cè)試函數(shù)fm（r）對(duì)方程（1）進(jìn)行檢驗(yàn)，可得如下矩陣方程

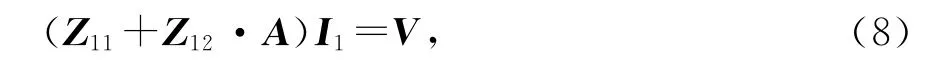
式中：Z11為MoM區(qū)的自阻抗矩陣；Z12和A分別為MoM區(qū)和PO區(qū)的互阻抗矩陣和耦合矩陣；I1為MoM區(qū)未知電流系數(shù)；V為激勵(lì)向量.

PO區(qū)電流系數(shù)I2則可由下式得到

由此可以看出，相比于傳統(tǒng)的MoM，MoM-PO將線性方程組的階數(shù)由（NMoM＋NPO）×（NMoM＋NPO）降至NMoM×MMoM.一般情況下NMoM?NPO，因此混合方法具有較高的計(jì)算效率.

1.2 梅利逼近

應(yīng)用MoM-PO混合方法分析寬帶電磁問(wèn)題時(shí)可得如下矩陣方程

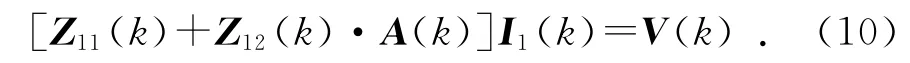
將MoM-PO與梅利逼近結(jié)合起來(lái)快速分析天線寬帶特性，其具體步驟為：

1）對(duì)于給定頻帶f∈［fa，fb］，對(duì)應(yīng)波數(shù)為k∈［ka，kb］，利用坐標(biāo)變換得

2）設(shè) Tl（）（l＝1，2，…，n）為l階切比雪夫多項(xiàng)式，其定義如下

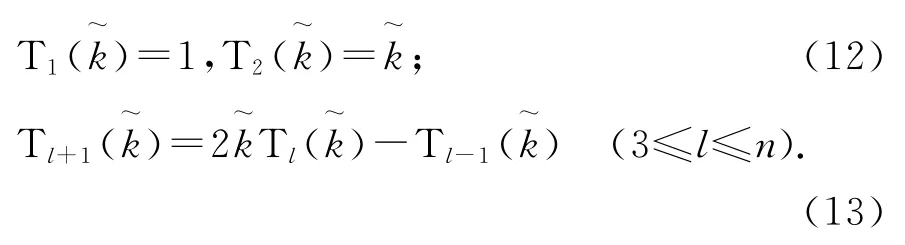
則n階切比雪夫多項(xiàng)式Tn）的n個(gè)零點(diǎn)i為

由此，可在［ka，kb］中確定n個(gè)切比雪夫節(jié)點(diǎn)，其表達(dá)式為

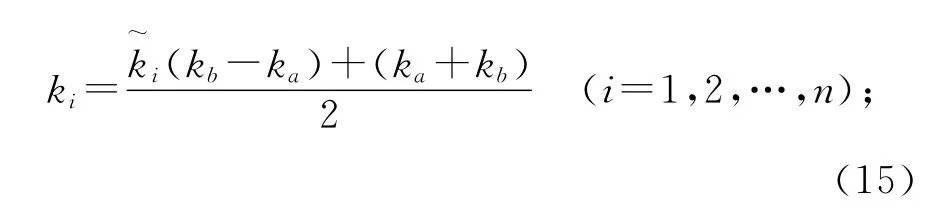
3）根據(jù)切比雪夫逼近，天線表面電流系數(shù)I1（k）可以表示為

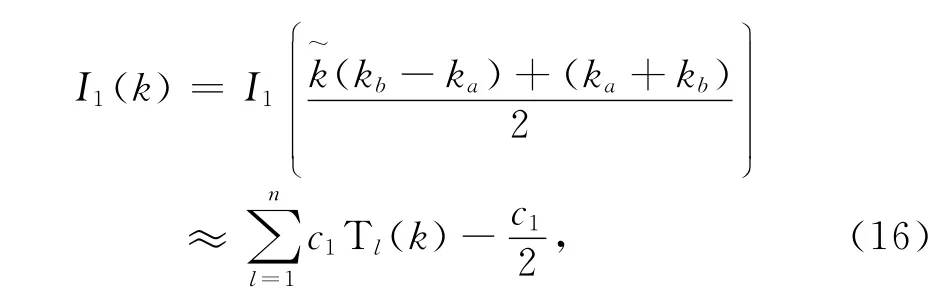
式中

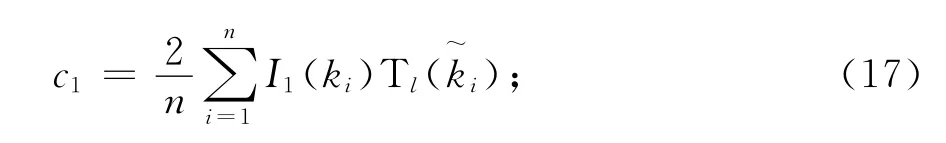
4）為提高計(jì)算精度，利用梅利有理展開(kāi)逼近電流系數(shù)矢量，則I1（k）可重寫(xiě)如下

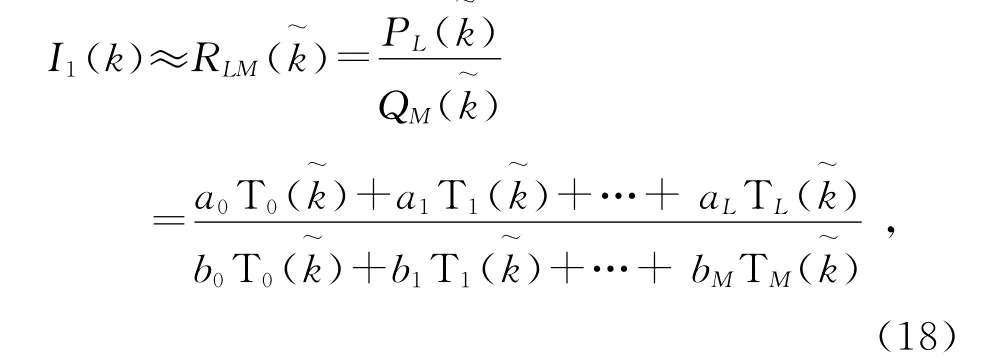
通常設(shè)b0＝1，將式（18）代入式（16）并利用恒等式TP（x）· Tq（x）＝（Tp＋q（x）＋T｜p-q｜（x））可得未知系數(shù)ai（i＝0，1，…，L）和bj（j＝1，2，…，M）如下：

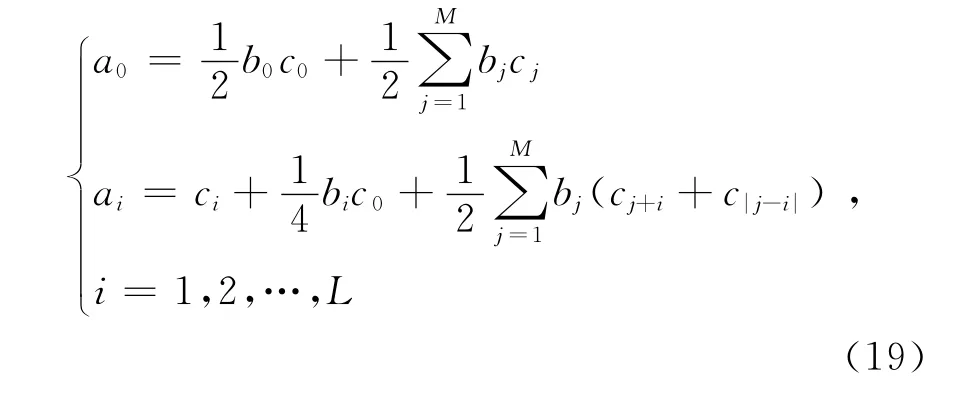
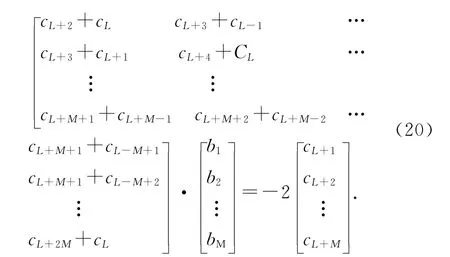
一旦有理函數(shù)系數(shù)ai和bj確定，將其代入式（18）即可求得給定頻域內(nèi)任意頻點(diǎn)的電流密度，進(jìn)而分析天線寬帶特性.

2 算例分析

圖1 導(dǎo)體板上方的對(duì)稱(chēng)振子天線

為驗(yàn)證算法的有效性，給出兩個(gè)算例的數(shù)值結(jié)果.所有計(jì)算都在主頻為2.8GHz的個(gè)人電腦上完成，迭代方法采用雙共軛梯度法，數(shù)據(jù)采用雙精度類(lèi)型存儲(chǔ).

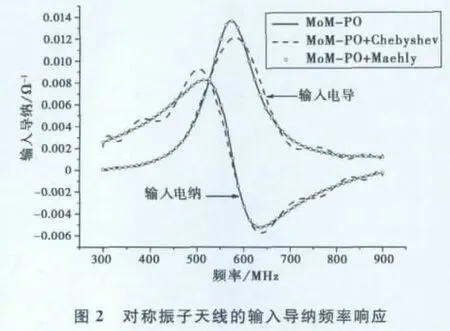
首先分析邊長(zhǎng)為2m的正方形理想導(dǎo)體平板上0.25m處水平放置的對(duì)稱(chēng)振子天線的寬帶輻射特性.對(duì)稱(chēng)振子天線利用長(zhǎng)為0.25m、寬為0.04m的細(xì)帶建模，天線剖分為32個(gè)三角形，共31未知量，而平板剖分為2 048個(gè)三角形，共3 012未知量，如圖1所示.利用MoM-PO方法進(jìn)行計(jì)算時(shí)，天線選為MoM區(qū)域，平板為PO區(qū)域，計(jì)算頻段為300～900MHz.圖2給出了采用逐個(gè)頻點(diǎn)計(jì)算、切比雪夫逼近（n＝12）和梅利逼近（L＝M＝4）三種方法得到的對(duì)稱(chēng)振子天線輸入導(dǎo)納頻率響應(yīng).可以看出：相比于切比雪夫逼近，梅利逼近與逐點(diǎn)計(jì)算的結(jié)果吻合更好，精度更高.將梅利逼近得到的天線工作在中心頻率600MHz時(shí)電場(chǎng)輻射方向圖（φ＝0°，0°≤θ≤180°）與測(cè)試結(jié)果對(duì)比于圖3.兩條曲線吻合良好，由于該算法沒(méi)有處理導(dǎo)體平板邊緣繞射場(chǎng)，所以后瓣部分存在誤差.

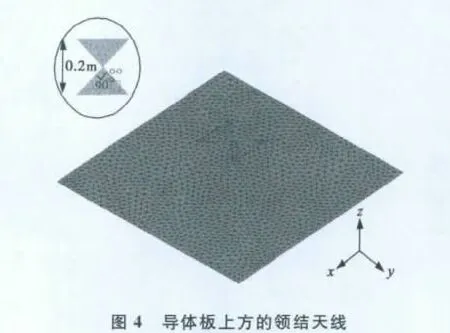
算例二考慮邊長(zhǎng)為1m的正方形導(dǎo)體板上0.24m處放置的領(lǐng)結(jié)天線.領(lǐng)結(jié)天線張角為90°，長(zhǎng)0.2m，天線剖分為94個(gè)三角形，共117未知量，而平板剖分為2 420個(gè)三角形，共3 566未知量，如圖4所示.天線為MoM區(qū)，平板為PO區(qū)，計(jì)算頻段為0.6～1.9GHz.圖5給出了領(lǐng)結(jié)天線的輸入導(dǎo)納頻率響應(yīng)曲線，圖6則為應(yīng)用梅利逼近方法得到的天線在xoz面輻射方向圖隨頻率變化情況.從表1可以看出：由于MoM-PO混合算法減少了未知量個(gè)數(shù)，導(dǎo)致內(nèi)存需求和計(jì)算時(shí)間比MoM有大幅度降低.如果進(jìn)一步采用梅利逼近方法快速掃頻，則可在160s內(nèi)獲取天線寬帶特性.

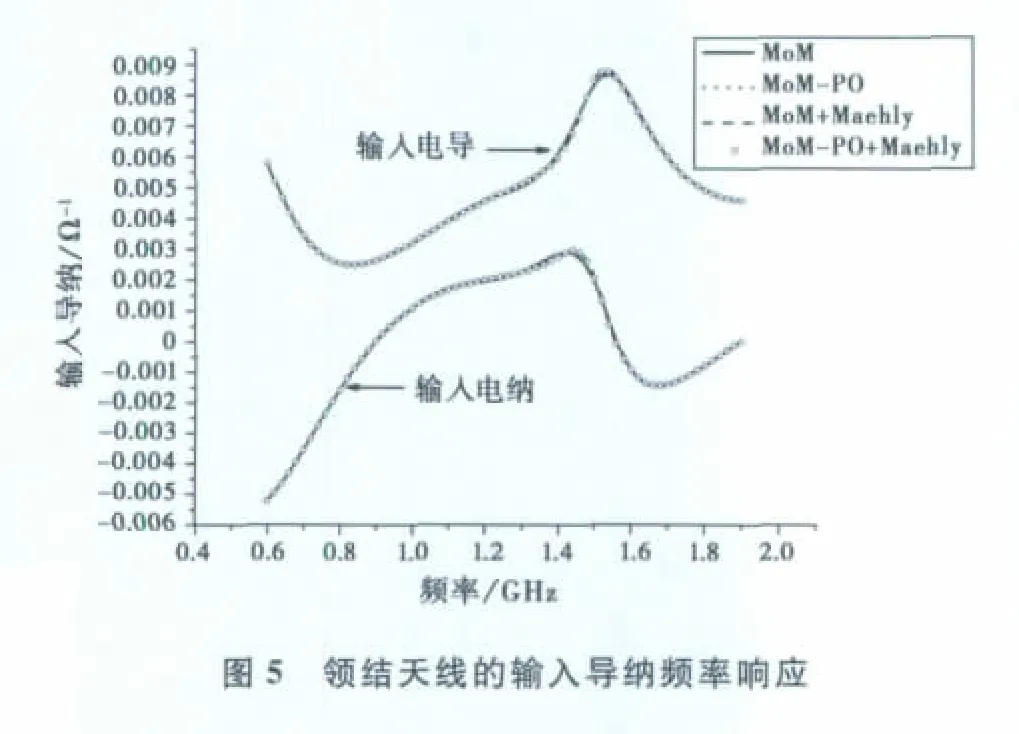
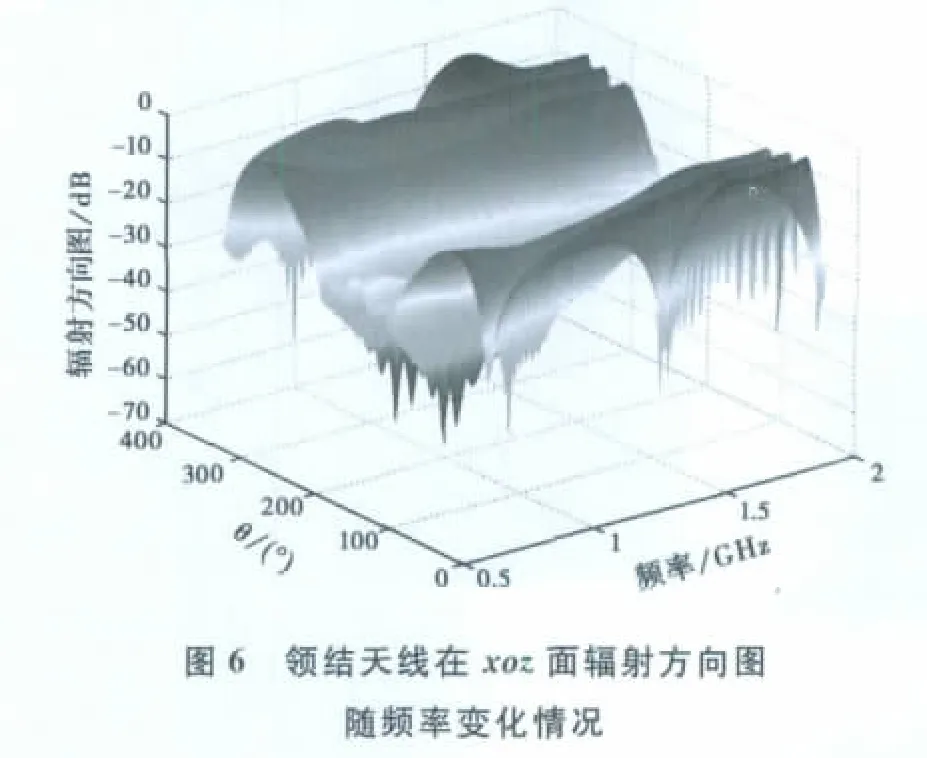
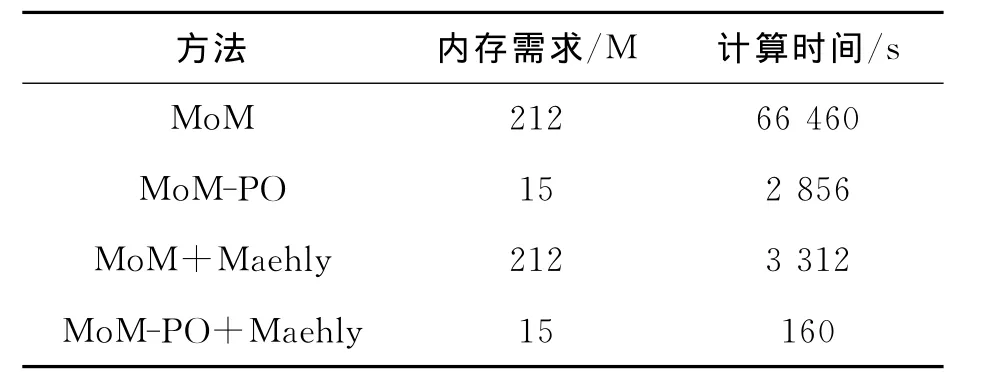
表1 算例二中不同方法內(nèi)存需求與計(jì)算時(shí)間對(duì)比

3 結(jié) 論

在切比雪夫逼近的基礎(chǔ)上，將梅利有理逼近引入MoM-PO混合方法中有效分析了載體平臺(tái)上天線的寬帶特性.數(shù)值結(jié)果表明：該方法的計(jì)算精度優(yōu)于切比雪夫逼近，而相比于逐點(diǎn)計(jì)算，該方法大大降低了求解時(shí)間.因此，MoM-PO結(jié)合梅利逼近分析載體平臺(tái)上天線特性對(duì)實(shí)際工程具有一定的指導(dǎo)意義.

［1］HARRINGTON R F.Field Computation by Moment Methods［M］.New York：MacMillan，1968.

［2］JAKOBUS U，LANDSTORFER F M.Improved PO MM hybrid formulation for scattering from three-dimensional perfectly conducting bodies of arbitrary shape［J］.IEEE Trans on AP，1995，43（2）：162-169.

［3］JAKOBUS U，LANDSTORFER F M.Improvement of the PO-MM hybrid method by accounting for effects of perfectly conducting wedges［J］.IEEE Trans on AP，1995，43（10）：1123-1129.

［4］翟會(huì)清，王莉娜，梁昌洪.利用UTD修正的MoM-PO混合算法研究［J］.電波科學(xué)學(xué)報(bào)，2003，18（5）：529-533.ZHAI Huiqing，WANG Li＇na，LIANG Changhong.A hybrid method of MoM and PO modified by UTD［J］.Chinese Journal of Radio Science，2003，18（5）：529-533.（in Chinese）

［5］陳海濤，羅建新，朱國(guó)強(qiáng).基于UV/MoM-PO的電大載體附近陣列天線的研究［J］.電波科學(xué)學(xué)報(bào)，2008，23（2）：292-295.CHEN Haitao，LUO Jianxin，ZHU Guoqiang.Analysis of array located near to electric large-scale platform based on UV/Mom-PO method［J］.Chinese Journal of Radio Science，2008，23（2）：292-295.（in Chinese）

［6］陳亞萍，孫厚軍，呂 昕.復(fù)合目標(biāo)模擬器電磁仿真的研究［J］.電波科學(xué)學(xué)報(bào)，2008，23（5）：808-811.CHEN Yaping，SUN Houjun，LüXin.Electromagnetic simulation of compound target simulator［J］.Chinese Journal of Radio Science，2008，23（5）：808-811.（in Chinese）

［7］BURKE G J，MILLER E K，CHAKRABARTHI S，et al.Using model-based parameter estimation to increase the efficiency of computing electromagnetic transfer functions［J］.IEEE Trans on Mag，1989，25（7）：2807-2809.

［8］REDDY C J，DESHPANDE M D，COCKRELL C R，et al.Fast RCS computation over a frequency band using method of moments in conjunction with asymptotic waveform evaluation technique［J］.IEEE Trans on AP，1998，46（8）：1229-1233.

［9］WANG Xing，GONG Shuxi，GUO Jingli，et al.Fast and accurate wide-band analysis of antennas mounted on conducting platform using AIM and asymptotic waveform evaluation technique［J］.IEEE Trans on AP，2011，59（12）：4624-4633.

［10］CHEN M S，WU X L，SHA W，et al.Fast and accurate radar cross-section computation over a broad frequency band using the best uniform rational approximation［J］.IET MAP，2008，2（2）：200-204.

［11］RAO S M，WILTON D R，GLISSON A W.Electromagnetic scattering by surfaces of arbitrary shape［J］.IEEE Trans on AP，1982，30（3）：409-418.