質(zhì)數(shù)p在正整數(shù)n中的最高指數(shù)

張光俊

（金陽(yáng)縣雙龍壩中學(xué)，四川 金陽(yáng) 616253）

質(zhì)數(shù)p在正整數(shù)n中的最高指數(shù)

張光俊

（金陽(yáng)縣雙龍壩中學(xué)，四川 金陽(yáng) 616253）

給出了質(zhì)數(shù)p在正整數(shù)n中的最高指數(shù)p(n)的定義，討論了p(n)的性質(zhì)，并給出了在整數(shù)的整除性方面的一個(gè)應(yīng)用.

質(zhì)數(shù)；正整數(shù)；最高指數(shù)；整除

1 引言與p(n)的定義

在文[1]P102中有如下定理：

定理A中[x]是實(shí)數(shù)x的取整函數(shù)，即[x]是不超過x的最大整數(shù).易知[x]有如下性質(zhì)：對(duì)任一實(shí)數(shù)x及任一正整數(shù)n都有[nx]≥n[x].

另外，定理A中采用了符號(hào)p(n!)來表示素?cái)?shù)（質(zhì)數(shù)）p在n!的標(biāo)準(zhǔn)分解式中的最高指數(shù)，這樣有pp(n!)|n!，但 pp(n!)+1n!.又由文[2]P88頁(yè)腳“恰整除”的概念知p(n!)恰整除n!.仿此我們引入質(zhì)數(shù)p在正整數(shù)n中的最高指數(shù)p(n)的定義，并研究其性質(zhì).

定義 設(shè)p是質(zhì)數(shù)，n正整數(shù)，r是非負(fù)整數(shù)，如果pr|n，但pr+1n，則稱r是p在n中的最高指數(shù)，簡(jiǎn)稱為p在n中的指數(shù)，記為p(n).

因此，定理A中p(n!)就是質(zhì)數(shù)p在n!中的指數(shù).結(jié)合文[2]P21的定理，定理A即為

定理Aˊ質(zhì)數(shù)p在n!中的指數(shù)為

由定義，對(duì)于給定的質(zhì)數(shù)p，p(n)是定義在一切正整數(shù)n上的一個(gè)非負(fù)整數(shù)函數(shù).若pn，由p0| n，則p(n)=0.若p|n，則n＞1，設(shè)n的標(biāo)準(zhǔn)分解式為

故p等于某一個(gè)且是唯一的一個(gè)pj(1≤j≤k)，由Pjαj

|n，p1,p2,…,pk是互異質(zhì)數(shù)，故，從而p(n)=pj(n)=αj.因此對(duì)任一正整數(shù)n總可以設(shè)其標(biāo)準(zhǔn)分解式為

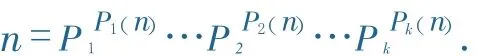
2 p(n)的性質(zhì)

定理1設(shè)p是質(zhì)數(shù)，n是正整數(shù)，r是非負(fù)整數(shù)，則p(n)=r的充要條件是：存在整數(shù)a使n=pra且pa.

證明：若p(n)=r，則pr|n，且pr+1n，所以存在唯一的正整數(shù)a使n=pra.如果p|a，設(shè)a=pb(b∈Z)，n=prpb=pr+1bpr+1|n，矛盾.故pa.

若存在整數(shù)a使n=pra且pa，則pr|n.如果pr+1|n，設(shè)n=pr+1b(b∈Z)，則pr+1b=prapb=ap|a，矛盾.故pr+1n，從而p(n)=r.

推論設(shè)p是質(zhì)數(shù)，n是正整數(shù)，則存在唯一的正整數(shù)a使n=pp(n)a且pa.

證明：由定理1，存在整數(shù)a使n=pp(n)a且pa，顯然a＞0，又由帶余除法知，整數(shù)a是唯一的.

定理2設(shè)p是質(zhì)數(shù)，m,n是正整數(shù)，則p(mn) =p(m)+p(n).

證明：由定理1的推論可設(shè)m=pp(m)a,pa，n=pp(n)b,pb，則mn=pp(m)+p(n)ab.如果p|ab，由p是質(zhì)數(shù)得p|a或p|b，矛盾.故pab，由定理1有p(mn)=p (m)+p(n).由定理2易得下面兩個(gè)推論（證明略）.

推論1設(shè)p是質(zhì)數(shù)，n1,n2,…,nk∈Z+，則

推論2設(shè)p是質(zhì)數(shù)，k，n∈Z+，則p(nk)=kp（n）.

定理3設(shè)p是質(zhì)數(shù)，m,n是正整數(shù)，且m|n，則

證明：因m,n∈Z+，且m|n，則n∈Z+，由定理m 2有

定理4設(shè)p是質(zhì)數(shù)，若n∈Z+是一個(gè)k次方數(shù)（即存在a∈Z+，使ak=n），則k|p(n)且p(n).

1

證明：因n∈Z+是一個(gè)k次方數(shù)，則nk∈Z+，由定理2的推論2有

證明：設(shè)小于等于n的質(zhì)數(shù)共k個(gè)，這k個(gè)質(zhì)數(shù)為p1,p2,…,pk，則n的標(biāo)準(zhǔn)分解式為

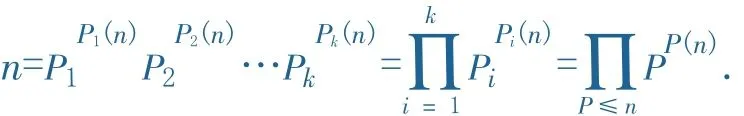
定理6設(shè)m,n∈Z+，p(m,n)是質(zhì)數(shù)p在最大公因數(shù)(m,n)中的指數(shù)，p[m,n]是質(zhì)數(shù)p在最小公倍數(shù)[m,n]中的指數(shù)，則

證明：（1）設(shè)m,n的標(biāo)準(zhǔn)分解式分別為

則

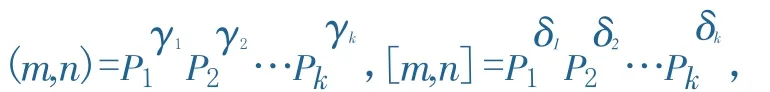
其中γi=min{pi(m),pi(n)}，δi=ma x{pi(m),pi(n)}，1≤i≤k.若p是某一pi，則

若p不同于p1,p2,…,pk，則

p(m,n)=0=p(m)=p(n)=p[m,n]，結(jié)論顯然成立.

（2）若p(m)≤p(n)，則min{p(m),p(n)}=p (m)，ma x{p(m),p(n)}=p(n)，由（1）有

p(m，n)+p[m，n]=min{p(m),p(n)}+ma x{p (m),p(n)}=p(m)+p(n).

若p(m)≥p(n)，則min{p(m),p(n)}=p(n)，ma x{p(m),p(n)}=p(m)，結(jié)論仍成立.

定理7設(shè)m,n∈Z+，則m|n的充要條件是對(duì)任一質(zhì)數(shù)p都有p(m)≤p(n).

證明：設(shè)m,n的標(biāo)準(zhǔn)分解式分別為則

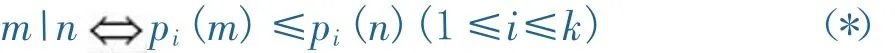
設(shè)m|n，若p是某一pi，則由（*）已有p(m)≤p (n)；若p不同于p1,p2,…,pk，則p(m)=0=p(n).

設(shè)對(duì)任一質(zhì)數(shù)p都有p(m)≤p(n)，則對(duì)質(zhì)數(shù)pi有pi(m)≤pi(n)(1≤i≤k)，由（*）有m|n.

定理8質(zhì)數(shù)p在正整數(shù)n中的指數(shù)為

證明：因(n-1)!|n!，由定理7及定理Aˊ得

下面舉一例來看定理7在整數(shù)的整除性方面的一個(gè)應(yīng)用.

例 證明(n!)(n-1)!整除(n!)!.

證明：設(shè)p為任一質(zhì)數(shù)，則

所以p((n!)(n-1)!)≤p((n!)!)，由定理7有(n!)(n-1)!|(n!)!.

京：高等教育出版社，1988.

[2]閔嗣鶴，嚴(yán)士健.初等數(shù)論（第三版）[M].北京：高等教育出版社，2003.

[1]余元希，田萬(wàn)海，毛宏德.初等代數(shù)研究（上冊(cè)）[M].北

TheMostSignificantofPrimeNumberp in Positive Integern

Z H A N G G uang j un
(J inyang C ounty S huanglong D am M iddle S chool,J inyang S ichuan616253)

I n this paper,themost signif icant p(n)of prime number pina positi v e integer n is defined,thenaturesof p(n)arediscussed,andanappl ication isgi v en in the integer di v isibleaspects.

P rime N umber;P ositi v e I nteger;M ost S ignif icant;D i v isible

O156.1

A

1672-2094(2013)01-0151-03

責(zé)任編輯：張隆輝

2012-12-28

張光俊（1982-），男，四川隆昌人，金陽(yáng)縣雙龍壩中學(xué)二級(jí)教師。