基于斯坦納樹的雷場網絡大面積損壞修復策略

董文，方向，范磊，楊力，雷志剛

(1.解放軍理工大學 野戰工程學院，江蘇 南京210007;2.中華人民共和國公安部 警衛局防爆安檢中心，北京100031)

0 引言

智能雷場一般通過人工布設預先設置在具有一定正面、縱深和布雷密度的場地。如圖1所示，以無線傳感器網絡為基礎的雷場網絡在戰場環境下易受到敵方爆破掃雷、電磁掃雷等破壞性攻擊，而導致大面積的雷場節點通信功能損壞，網絡被分割成若干個互不相連的部分，智能雷場失去了整體協調攻擊地面裝甲目標的能力。

圖1 被分割為數個互不相連的部分的受損雷場網絡示意圖Fig.1 Articulation of a damaged minefield network that was partitioned into multiple disjoint segments

在傳統無線傳感器網絡中，當少量節點損壞時，通常采用調大節點功率的方式來愈合失效拓撲。然而遭受大面積節點損壞的雷場網絡卻無法通過該方式來愈合拓撲。目前各國都在研制具有自主移動能力的節點［1-3］，稱之為中續節點。該類節點在網絡完好的情況下處于休眠狀態，當網絡遭到破壞時，能夠按照特定策略遷移至指定位置替代受損節點，由該類節點進行的拓撲修復不僅能夠使全局拓撲恢復連通性，還能讓恢復的網絡通信路徑長度變短，從而更加節省網絡能耗。目前關于網絡拓撲修復的研究較為薄弱，文獻［4］采用STP-MSP 算法建立一顆包含網絡節點和斯坦納(Steiner)點的Steiner 樹，選擇并調度一些節點移動到這些Steiner 點上，從而修復網絡拓撲。文獻［5］采用近似算法，首先找到各相鄰片區的最優Steiner 點位置，再對各點使用質心量算方法獲取最優解，解決水下無線傳感器網絡的拓撲修復問題。文獻［6］針對網絡中某個節點失效而造成網絡連接中斷的情況，采用啟發式算法CRR 指導對失效節點的鄰居節點向指定地點移動，從而恢復網絡連通性，并且恢復后的網絡擁有更好的負載均衡性。

離散量子粒子群優化算法是由Yang 等于2004年提出的［7］，是量子粒子群優化算法在離散問題上的改進算法。算法將量子粒子群算法中的粒子離散化，成為離散的粒子矢量。蛙跳優化算法在離散問題上的應用是由Martinez-Garcia 等于2008年提出的［8］，蛙跳優化算法的原理是，將整個青蛙群體按照一定規則劃分成若干個子群，子群獨立進化，一定階段后，再融合在一起，重新劃分后再獨立進化，直到滿足結束條件。二者都采用組織社會行為代替進化算法的自然選擇機制，但在算法表現方面有著不同的特點。離散量子粒子群優化算法(QDPSO)簡潔效率高，局部搜索速度快，但會由于粒子在運動過程中產生惰性而發生早熟收斂，導致陷入局部最優解。蛙跳優化(JFO)的局部搜索速度較慢，但其采用多種群的進化方法，擁有優良的全局搜索性能。蛙跳和離散量子粒子群混合優化(JF-QDPSO)算法采用二者相結合的方法，利用QDPSO 算法進行子群內部局部搜索，利用JFO 的多子群進化方法進行子群間的混選，跳出局部最優，以達到收斂速度快及全局搜索性能好的目的。

本文針對網絡節點受到大面積損壞的情況，將網絡拓撲愈合問題映射到斯坦納最小樹(SMT)問題，通過引入JF-QDPSO 算法求解中續節點位置，修復網絡拓撲。該策略采用群體智能算法，具有執行簡單、計算時間短以及恢復后的網絡平均通信鏈路小等優點，具有較強的實用性。

1 問題描述及轉化

設智能雷場網絡中共有N 個具有移動和定位能力的中續節點，當網絡遭到攻擊被分割成數個互不連通的部分后，需要啟動中續節點來代替受損節點修復網絡拓撲。這里忽略智能雷場節點隨即拋灑布設的情況，僅考慮人工定點布設節點。就該問題而言，扮演替代角色的中續節點的位置選取至關重要，節點的遷移行為不僅需要恢復受損拓撲，更能使修復的網絡節省能耗，縮短網絡通信鏈路長度，因此智能雷場網絡修復問題可歸結為最優化網絡拓撲的中續節點位置選取問題。對于此類連通數個被分割的部分形成通路的最優問題，通常都被歸為SMT［9-10］問題。

定義1 給定圖G =(V，E)，V 為圖G 的節點集，E 為圖G 的邊集，費用函數C:E→R+，R+為正實數，目標節點集D?V.則SMT 為從圖G 中找出連通D 中所有節點的最小生成樹，即使樹的費用最小，則該最小生成樹稱為SMT.

然而，根據智能雷場網絡通信的特殊性，需要規定每個連通節點間的距離d(i，j)最多不能超過通信距離R，且費用函數C 的最小值即為所形成的連通網絡通信鏈路長度最小值。

定義2 抽象受損智能雷場網絡為圖G =(V，E，C).其中:V 表示節點集，E 表示節點間的無線鏈路集合，C 為費用函數，表示所有無線鏈路的總長度。滿足:eij表示節點i，j 之間的鏈路，目標節點集D?V.因此，智能雷場網絡大面積受損修復問題被轉化為:確定中續節點的位置，使得在圖G 中能夠形成一個連通所有目標節點的子樹T，且所有無線鏈路總長度最小，即

2 基于區域網格模型的JF-QDPSO 算法

2.1 標準粒子群算法

粒子群算法是由Kennedy 等［11］提出的一種智能優化算法，優點為算法簡潔，易于實現，且沒有梯度信息。該算法通過初始一群隨機粒子(每個粒子代表著一個潛在解)，并利用迭代方式，使每個粒子向自身找到的最好位置和群體中最好粒子靠近，從而搜索最優解。標準粒子群算法迭代過程如下

式中:vij為第i 個粒子j 維的飛行速度;xij為粒子位置;k 為迭代次數;r1和r2為［0，1］之間的隨機數;c1和c2為加速因子;pbest是粒子i 迄今為止搜索到的最優位置;gbest為整個粒子群迄今位置搜索到的最優位置。

2.2 雷場網絡模型

本文關注的核心問題是中續節點的放置位置，假若雷場網絡中節點隨意放置，會使得算法的搜索空間無限大，不利于實際工程問題的解決。為了縮小算法搜索空間規模，本文將雷場網絡的節點放置網格化。圖2顯示了網格型的智能雷場網絡結構，中續節點的可能放置位置必須在網格交點處，且單位網格長度等于節點間通信距離R.

2.3 蛙跳和離散量子粒子群混合優化算法

通過將雷場區域網格化，放置中續節點的位置由連續空間變為可供選擇的離散點，因此，本文采用QDPSO 和JFO 相結合的算法解決雷場網絡修復問題。

JF-QDPSO 算法的粒子群表述為

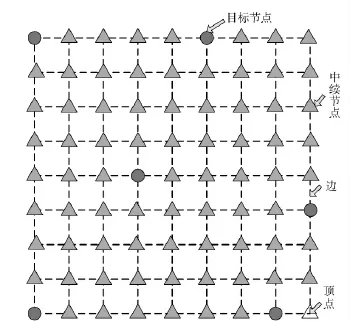
圖2 基于網格模型的雷場網絡結構Fig.2 Grid-based minefield network architecture

式中:S 為整個青蛙種群;K 為子群數量;m 為單個子群所包含的粒子規模;Xki表示單個粒子位置。在智能雷場網絡大面積受損修復問題中，單個粒子位置由一串離散的二進制碼表示Xki=［xki1，xki2，…，］，n 為中間節點的數量，此處xkij只能取0 或者1.當xkij取1 時，表示中間節點j 被選擇為中續節點的放置位置，當xkij取0 時，則在該節點處不放置中續節點。

JF-QDPSO 不采用標準粒子群算法的粒子飛行速度來更新粒子，取而代之的是粒子從一個可行解跳躍到另外一個可行解。每個粒子Xi跳躍到下一時刻位置Xi+1由以下3 種變量決定:該粒子迄今為止搜索到的最好位置b;子群內部所有粒子迄今為止搜索到的最好位置gi;整個種群所有粒子迄今為止搜索到的最好位置g*.

本文提出的算法1～3 顯示了JF-QSPSO 求解雷場網絡大面積損壞修復問題的具體細節。算法1 是算法的主體結構，算法2 保證經過每次跳躍過程后Xi+1也是問題的可行解，算法3 起到本地搜索的作用，在滿足問題可行解的前提下盡可能多的除去被選中的中續節點。

算法首先產生一個規模為m 的子群S，初始化粒子X1為［1，1，…，1］，因此X1必然是該問題的一個可行解。在的每一次迭代過程中，原先粒子位置Xi經過一次隨機跳躍，變成另外一個可行解Xi+1.隨機跳躍過程是由一個在0 和1 之間的隨機數ξ 控制的，算法等概率的在Xi、bi、gi、g*之中選擇一個數為selected.隨后執行Combine(Xi，selected)(見算法2)將粒子Xi與被選擇粒子selected 結合起來。這里運用到了comp(Xi)的概念［12］，它表示至少包含一個目標節點的斯坦納連通圖，當且僅當comp(Xi)=1 時，Xi才是問題的一個可行解。算法2 首先在［0，num(|Xi|)］之間選擇一個隨機數ψ，隨后從集合|Xi|隨機刪除一個中續節點，或者從集合selected 中隨機增加一個節點為中續節點，此操作循環ψ 次后終止。隨后更新Xi及comp(Xi)，如果Xi是非可行解時(comp(Xi)＞1)，隨機添加一個節點為中續節點，直到得到可行解(comp(Xi)=1).算法3 起到了一個本地搜索的作用，在不影響解可行性的前提下，盡量縮小中續節點數量。本地搜索之后，變量(bi，gi，g*)都會被更新，用到下一次循環當中。這里，循環的次數可以理解為子群的數量，當循環次數達到指定的子群數量或者得到了滿意的g*，則循環中止，輸出斯坦納樹T.

1)算法1:蛙跳和離散量子粒子群混合優化算法求解雷場網絡大面積損壞快速修復問題。

輸入:網格劃分后的連通權重圖G =(V，E，C)，其中包含了n 個頂點，l 條邊，以及Q?V 個目標節點;

輸出:連通所有目標節點且權重值最小的斯坦納樹T;

初始化:令|Xi|為中續節點的集合，即|Xi| ={xij=1/xij，j =［1，n］};令C(Xi)為粒子Xi的適應度函數，C(Xi)=隨機產生子群Sk粒子規模m，Sk=［Xk1，Xk2，…，Xkm］.

-運行算法2Combine(Xi，selected)，將粒子Xi與被選擇粒子selected 結合起來;

-運行算法3Local-Search(i，Xi)，進行本地局部搜索;

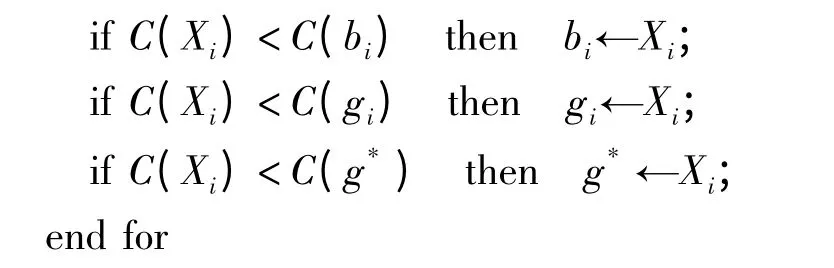
until 達到循環中止條件;

-輸出斯坦納樹T=G(|g*|，E(|g*|))，其中E(|g*|)為連接g*中的中續節點且邊長小于等于通信距離R 的邊。

2)算法2:Combine(Xi，selected)

-令comp(Xi)為至少包含一個目標節點的斯坦納連通圖;令num(|Xi|)為集合|Xi|中中續節點的數量;在［0，num(|Xi|)］之間選擇一個隨機數:ψ←Random(0，num(|Xi|));

3 仿真實驗

平均鏈路長度和平均計算時間是評價雷場網絡修復算法的重要參數。鏈路長度短說明在能夠保證重建網絡連通的前提下，運用的節點數量少，且修復后的網絡通信能耗小，生存周期長;計算時間少則表明算法執行時間短，算法效率高。

為了驗證JF-QDPSO 的性能，針對中間節點數{100，400}和目標節點數{5，8，10}6 個樣本，對SMT-MSP［10］(Steiner minimum tree with minimum number of Steiner points)、QDPSO 和JF-QDPSO 進行比較，其中JF-QDPSO 的種群規模為100，分成20 個子群，最大迭代數1 000.PC 機平臺為Pentium 4 CPU，主頻1.43 GHz，內存1 GB，操作系統使用Windows XP，利用Visual C + +6.0 語言編程實現。表1給出了SMT-MSP、QDPSO 和JF-QDPSO 對六個樣本仿真計算100 次得出的平均網路鏈路長度和平均計算時間。從表1中可以看出:JF-QDPSO 和QDPSO 不僅從計算結果，而且在計算時間上也遠遠勝過SMT-MSP，這表明離散量子粒子群算法比啟發式算法SMT-MSP 簡潔高效，且能夠更好的應用于雷場網路拓撲修復中。此外，從JF-QDPSO 與QDPSO的比較來看，JF-QDPSO 在求解結果上比QDPSO 更優，然后求解速度上卻因多子群間的協作進化而略低于QDPSO.

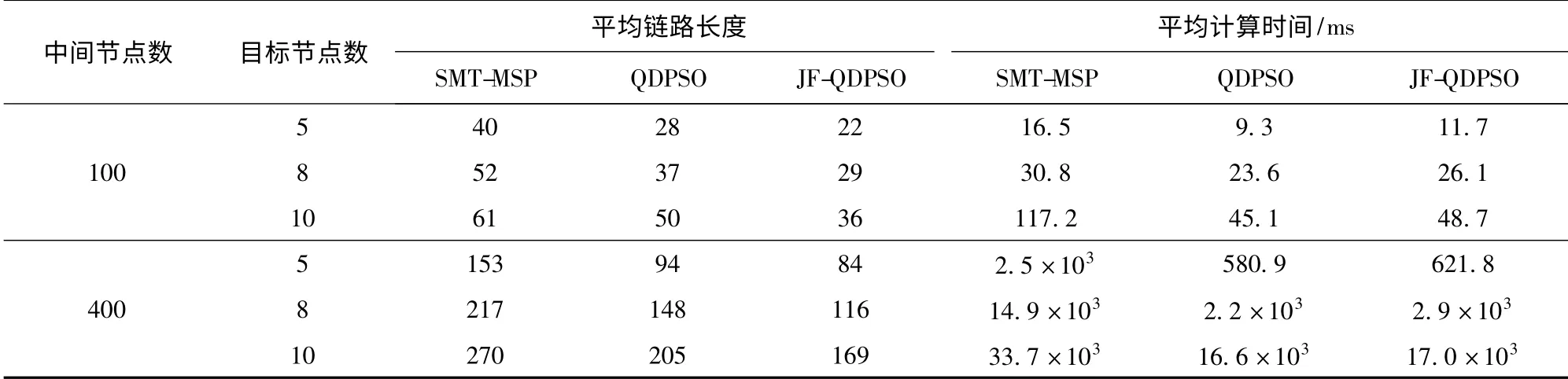
表1 3 種算法對不同樣本的平均鏈路長度和計算時間Tab.1 Average link length and computational times with different samples for three algorithms

圖3給出了在中間節點數為100，目標節點數為5 的情況下3 種算法的收斂曲線。圖中，SMTMSP 在95 代左右才趨近于收斂，且結果最差;QDPSO 在40 代左右就趨近于收斂，但效果一般;JFQDPSO 在60 代左右趨近于收斂，且效果最好，這說明蛙跳算法與離散量子粒子群算法的結合，有效克服了算法陷入局部最優解，體現了其收斂速度快及全局搜索性能好的特點。

圖3 3 種算法的收斂曲線Fig.3 Convergence performance for three algorithm

4 結論

本文研究了以無線傳感器網絡為基礎的智能雷場網絡大面積損壞拓撲修復問題。將該問題抽象為求解斯坦納最小樹問題，提出了蛙跳和離散量子粒子群混合優化算法。理論和數值仿真證明，該算法充分利用了粒子群算法收斂速度快、局部搜索能力強以及混合蛙跳算法全局尋優能力強、跳出局部最優能力好的特點，較SMT-MSP 算法在平均鏈路長度上較低了43.2%，在平均計算時間上降低了51.4%.可見，本文所提算法在有效恢復網絡拓撲的同時，降低了恢復后網絡的通信荷載，延長了網絡生存周期。

References)

［1］ Mattias S，Mathias B，Alessandro Si，et al.An autonomous spherical robot for security tasks［C］∥2006 IEEE International Conference on Computational Intelligence for Homeland Security and Personal Safety.AV Alexandria，AV:IEEE，2006:1233 -1236.

［2］ Sugiyama Y，Hirai S.Crawling and jumping by a deformable robot［J］.International Journal of Robotics Research，2006，25(5):603 -620.

［3］ 付夢印，楊毅，朱昊，等.移動機器人組合感知系統及其配準方法改進［J］.兵工學報，2011，32(6):712 -718.FU Meng-yin，YANG Yi，ZHU Hao，et al.Integrated perception system for mobile robot and its improved registration［J］.Acta Armamentarii，2011，32(6):712 -718.(in Chinese)

［4］ Cheng X Z，Du D Z，Wang L S，et al.Relay sensor placement in wireless sensor networks［J］.Wireless Netwroks，2008，14(3):347 -355.

［5］ 劉林峰，劉業.基于滿Steiner 樹問題的水下無線傳感器網絡拓撲愈合算法研究［J］.通信學報，2010，31(9):30 -45.LIU Lin-feng，LIU Ye.Study of topology recovery algorithm based on full Steiner minimum tree problem in underwater wireless sensor networks［J］.Journal of Communications，2010，31(9):30 -45.(in Chinese)

［6］ Mohamed Y，Rahul W.Connectivity restoration in wireless sensor networks using Steiner tree approximations［C］∥IEEE Global Telecommunications Conference.Miami:IEEE，2010:1 -5.

［7］ Yang S，Wang M，Jiao L.A quantum particle swarm optimization［C］∥Proceeding of the 2004 IEEE Congress on Evolutionary Computation.Alexandria:IEEE，2004:320 -324.

［8］ Martunez-Garcia F J，Moreno-Perez J A.Jumping frogs optimization:a new swarm method for discrete optimization［C］∥Teth.Rep.DEIOC 3/2008，Dep.Of Statistics，O.R.and Computing.Spain:University of La Laguna，2008:29 -46.

［9］ Lin G，Xue G.Steiner tree problem with minimum number of Steiner points and bounded edge length［J］.Information on Processing Letters，1999，69(2):53 -57.

［10］ Lloyd E L，Xue G.Relay node placement in wireless sensor networks［J］.IEEE Transcations on Computers，2007，56(1):134 -138.

［11］ Eberhart R，Kennedy J.A new optimizer using particle swarm theory［C］∥Proceeding of the Sixth International Symposium on Micro Machine and Human Science.Nagoya:Indianapolis Press，1995:39 -43.

［12］ Cerulli R，Fink A.Extensions of the minimum labelling spanning tree problem［J］.Journal of Telecommunications and Information Technology，2006，32(4):39 -45.