EMD過程中數據擬合的算法改進與實現*

寇艷廷，范濤濤，劉 晨，閻紅燦

（河北聯合大學 理學院，河北 唐山 063000）

希爾伯特—黃變換HHT（Hilbert-Huang Transform）是1998年由Huang等人[1-2]提出的一種信號分析方法，它通過經驗模態分解EMD（Empirical Mode Decomposition）基于信號的局部特征時間尺度將信號分解成有限數目的本征模態函數 IMF（Intrinsic Mode Functions）之和，對每個IMF進行Hilbert變換可以求得具有物理意義的瞬間頻率，非常適合對非平穩信號處理。所以許多研究學者將該技術應用于數據波的時頻分析[3-4]和時間序列的預測研究[5-6]，取得了顯著的成果。

時間序列模型適合于線性時序的預測，當用于預測非線性時間序列時，準確性較差；小波分析方法中數據基本假定為平穩序列，當用于非平穩時間序列預測時準確性不高；神經網絡具有逼近非線性的能力，然而當用神經網絡來預測股價時間序列時，其結果不是很理想；中國證券市場的混沌性暗示著金融時間序列的長期不可預測性和短期預測的可行性，但混沌模型與其他方法對股市進行預測時，也未能得到令理論界和實務界較滿意的效果。在研究金融數據預測時提出了將EMD與神經網絡結合的預測模型，就是利用EMD處理非平穩數據的優勢。

在EMD過程中，最為關鍵的就是如何擬合成與原始數據逼近的函數，即構造函數的算法問題。而要想構造較為準確的函數，關鍵是包絡線的選取算法。現有的EMD分解算法一般應用三次樣條插值法，雖然能夠得到較為理想的結果，但仍然有些偏差，特別是邊緣數據（拐點）誤差較大。本文系統分析了三次樣條插值算法和分段冪函數插值算法的特點，將其結合找到一種更好的求包絡線的算法，從而提出了一種更為有效的數據擬合函數構造方法。

1 經驗模態分解（EMD）

1.1 本征模態函數性質

EMD算法的目的就是將復雜數據（信號）分解為有限個本征模態函數IMFs，這里IMF須滿足如下兩個性質：

（1）信號的極值點（極大值或極小值）數目和過零點數目相等或最多相差一個；

（2）由局部極大值構成的上包絡線和由局部極小值構成的下包絡線的平均值為零。

1.2 EMD算法簡介

EMD算法步驟如下：

（1）計算出信號 s（t）所有的局部極值點。

（2）求所有的極大值點構成的上包絡線和所有的極小值點構成的下包絡線，分別極為 u0（t）和 v0（t）。

（3）記上、下包絡線的均值為：

（4）判斷 h0（t）是否滿足 IMF的上述兩條性質。若滿足，則 h0（t）為 IMF；否則，記 h0（t）為 s（t）。 重復步驟（1）~步驟（3），直到得到一個 IMF，記為 C1（t）。

（5）記 r1（t）=s（t）-C1（t）為新的待分析信號，重復步驟（1）~步驟（4），以得到第二個 IMF，記為 C2（t），此時余項 r2（t）=r1（t）-C1（t）。 重復上述步驟，直至得到的余項 rn（t）是一個單調信號或 rn（t）的值小于預先給定的閾值，分解結束。

如此，最終可得到 n 個 IMFs，C1（t），C2（t），…，Cn（t）余項為 rn（t）。 因此，原信號 s（t）可表示為：

2 分段冪函數插值算法的應用

EMD算法的核心部分就是求解包絡線算法，現有的技術一般采用三次樣條插值法。由于邊緣數據（端點）選取直接影響數據擬合效果，如果樣條插值中端點的選取再精確些，就會得到更好的擬合數據點，而分段冪函數具有端點延拓的特點，對邊緣端點有平滑處理功能，彌補了樣條插值法的缺陷。本節詳細討論分段冪函數插值在求解包絡線中的應用。

2.1 算法原理及分析

記所有的插值點 P1（x1，y1），P2（x2，y2），…，Pn（xn，yn），插值函數 y=f（x）。對任意 3 個相鄰點 Pi-1（xi-1，yi-1），Pi（xi，yi），Pi+1（xi+1，yi+1）進行冪函數插值：

分段冪函數插值算法的誤差范圍隨β的增大而減小，且誤差的最大范圍為[Mh2/2.5，5Mh2/2]。

2.2 算法實現

3 實驗仿真

結合實際數據，利用Matlab數學軟件進行實驗仿真，表1是實驗仿真的測試數據。

表1 數據記錄表

3.1 利用三次樣條插值函數繪制圖像

選擇Matlab內置函數spline，先編寫主函數，核心代碼如下：

以文件名yangtiao_main.m保存。運行程序，得到運行結果如圖1和圖2所示。

3.2 利用分段三次樣條插值保形：

主函數核心代碼： %分段三次Hermite插值法主函數

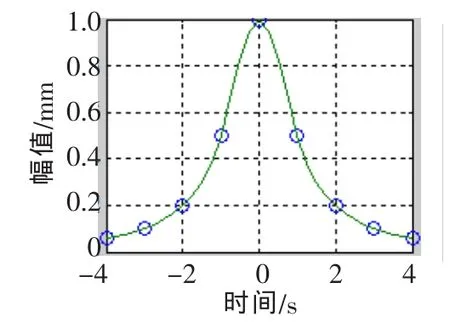
圖1 三次樣條插值采樣點

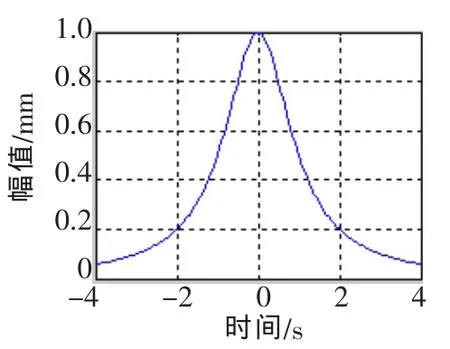
圖2 三次樣條插值擬合結果

運行程序，結果如圖3和圖4所示。

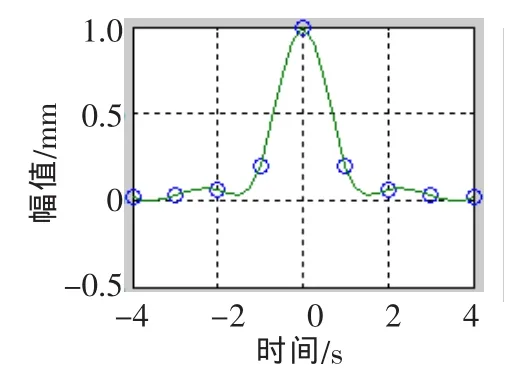
圖3 分段冪函數采樣點

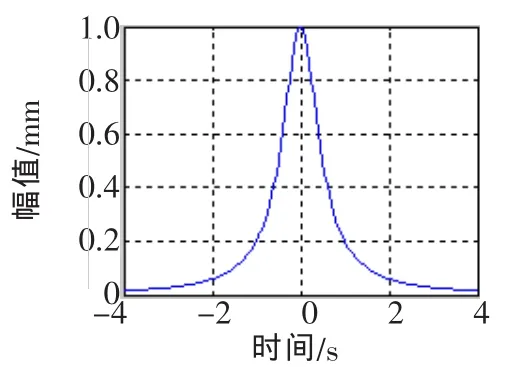
圖4 分段冪函數擬合結果

3.3 實驗分析

從圖1可以看出，經過分段冪函數的端點延拓處理，插值擬合的函數更接近于原始數據，大大提高了EMD中數據擬合的效果。為下一步數據分析和預測提供了技術保證。

本文在分析經驗模態分解算法的基礎上，討論了三次樣條插值求解包絡線的弊端，引入分段冪函數端點延拓技術，提高了數據擬合精度。實驗表明，對數據擬合算法的改進極大提高了EMD過程中函數擬合的效果，有利于提高時間序列分析和預測精度。

[1]HUANG N E， Shen Zheng， LONG S R， et al.The empirical mode decomposition and the Hilbert spectrum for non-linear and non-station time series analysis[J].Proc R SocLond，1998，45（4）：903-995.

[2]HUANG N E， Shen Zheng， LONG S R.A new view of non-linear water waves.The hilbert spectrum [J].Annual Review of Fluid Mechanics，1999，31：417-457.

[3]蓋強.局域波時頻分析方法的理論研究與應用 [D].大連：大連理工大學，2001：52-54.

[4]徐世艷.經驗模態分解的時頻分析方法及其應用[J].吉林大學學報，2009，9（27-5）：487-492.

[5]劉慧婷，倪志偉，李建洋.經驗模態分解方法及其應用[J].計算機工程及應用，2006，32（1）：44-47.

[6]玄兆燕，楊公訓.EMD在地面氣溫預測中的應用 [J].微計算機信息，2008，2（24-3）：230-232.