基于可靠性理論的被腐蝕鋼筋混凝土結構維修次數優化

李 暉，滕海文，2，趙 卓，賀志遠，霍 達，2

（1.北京工業大學 建筑工程學院，北京100124；2.北京工業大學 工程抗震與結構診治北京市重點實驗室，北京100124；3.鄭州大學 土木工程學院，鄭州450001）

確定合理的維修時間點及維修次數不僅可以延長結構的使用年限，還能夠降低建筑物的日常維護成本。Nader等［1］考慮了定期或不定期的維修時間間隔對結構的影響，并通過結構的性能指標來尋求最佳的維護策略。Michael等［2］認為最佳維修時間和修復程度的確定應主要依據結構的最佳收益率。Mullard等［3］針對受腐蝕鋼筋混凝土結構的維修效率進行了研究，提出以被腐蝕結構出現開裂為維修時間點為確定依據。謝桂華等［4］采用概率網絡估算法對被腐蝕混凝土結構的動態可靠度及維修決策方法進行了研究。秦劍君等［5］運用群體多目標規劃理論推導了建立被腐蝕結構維修策略模型的全過程。

目前，國內外針對一次性維修的優化研究較多，但由于被腐蝕結構所處的環境各不相同，各個結構的腐蝕速率也不同。對于那些長期受到嚴重侵蝕的結構，如果在結構服役期間僅考慮進行一次維修加固是不適合的。如何確定每個被腐蝕結構在其設計基準期內的最優維修次數就成了一個亟待解決的問題。本工作針對目前結構僅考慮一次維修加固的不足，討論了被腐蝕結構在其服役過程中經多次維修的動態可靠度變化規律，提出了被腐蝕結構在其設計基準期內考慮維修加固處理條件下的最優維修次數的實用方法，對被腐蝕結構合理優化維修次數具有一定的理論意義和實用價值。

1 被腐蝕鋼筋混凝土結構多次維修的動態可靠度衰減規律

在腐蝕性介質環境影響下，結構或構件的及抗力荷載效應均表現為一隨機過程［6］。在任意一次維修時間點表現為一隨機變量，假定在任意一次維修時間點（t＝tn），抗力及荷載效應均服從正態分布，則采用一次二階矩方法［7］。計算結構n次維修的動態可靠性指標的公式為：

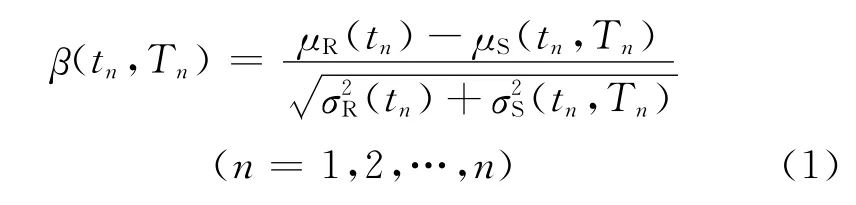
式中：β（tn，Tn）——已服役時間為tn、后續使用時間為Tn時結構的動態可靠度指標；μR（tn），σS（tn）——服役時間為tn時，結構抗力變量的均值和標準差；μS（tn，Tn），σS（tn，Tn）——服役時間為tn、后續使用時間為Tn時，結構荷載效應變量的均值和標準差。

對上述關系式進行簡化，近似認為荷載效應變量的均值與方差均為常數，不隨服役時間而改變，故受腐蝕結構n次維修的動態可靠度即是結構服役時間的函數。

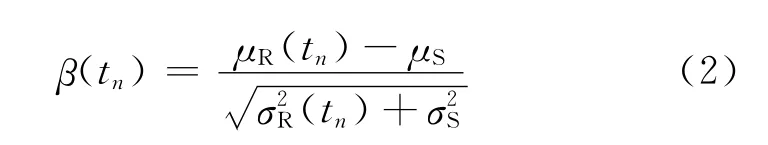
對于被腐蝕結構，其綜合動態承載能力是從結構正常承載力水平開始逐漸降低的。因此被腐蝕結構從投入使用到完成設計基準期的時間區段T內，結構可靠度水平的衰減量為［8］

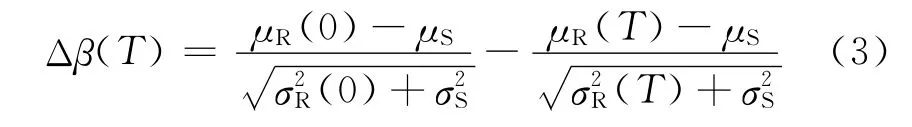
由此可見，受腐蝕結構的動態可靠度隨服役時間的變化規律主要取決于結構承載能力均值和標準差隨時間而變化的特點。

2 考慮多次維修條件下的優化設計

若假定在結構設計基準期內需進行多次維修，則與結構設計可靠度、多次維修的時間點、維修可靠度水平等參數完全相關。若以T表示已確定的結構設計基準期，tn表示結構多次維修的時間點，則維修目標所確定的結構后續使用時間為Tn＝T-tn。以C（0，T），（tn，Tn）分別表示結構的直接費用和多次性維修費用的總和，以表示結構n次維修所需要的時間（年），U表示正常條件下，該結構的年使用效益，則n次維修而導致的使用效益的損失為tncU，考慮n次維修情況下，被腐蝕結構總效益的優化設計與維修決策目標函數可表示為：

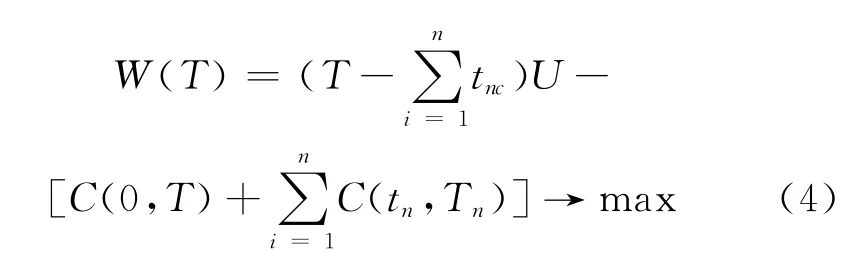
通常情況下，結構在設計基準期內的維修次數不會超過三次，當結構的維修次數n≤3時，結構的總維修時間與設計基準期相比較小，為簡化計算將其忽略不計。則使上述優化目標函數取極大值等價于：

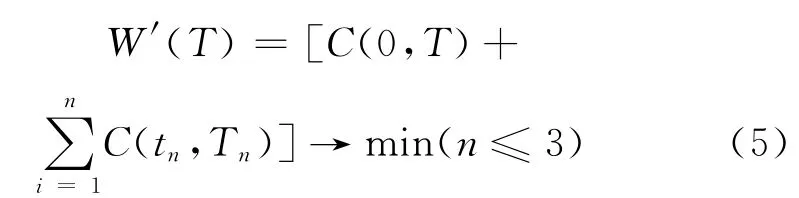
文獻［9］研究并建立了設計可靠度與結構造價之間的函數關系以及結構維修費用與維修可靠度間的函數關系。

當結構設計可靠度取時，造價則可表為［9］：

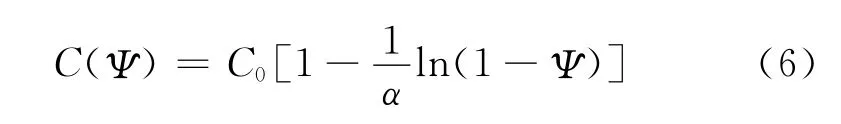
式中：C0表示結構可靠度趨近于零時的結構造價，根據近似工程經驗及專家判斷，對其進行大致估計。

當在時刻tn對結構進行維修，將其可靠度水平Ψn由提高到Ψ′n時，維修費用可表為：

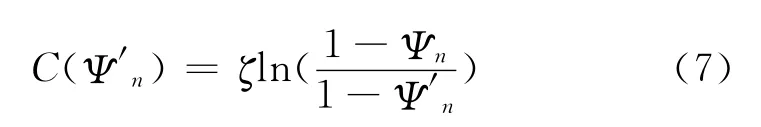
式中：ζ表示結構維修后的失效概率為維修前失效概率的0.368倍時所需要的維修費用，其值可利用綜合評定和專家經驗來進行評估；Ψn，Ψ′n分別表示結構第n次維修前后的可靠度水平。

上式（5）則可進一步表示為：

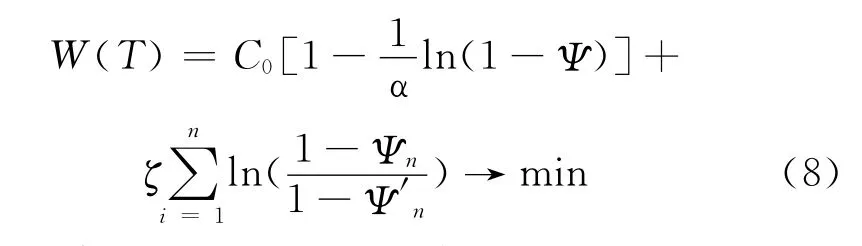
此式建立了結構設計可靠度、n次維修時刻可靠度及維修后結構可靠度與優化設計目標函數之間的顯式函數關系。但由于建筑結構腐蝕過程的復雜性，使得建筑結構可靠度隨服役時間的變化規律難以用簡單的函數式表達，因此上式具有定性意義，如果要進行定量的優化設計還需作進一步簡化。

通常情況下，建筑結構的設計基準期是由設計工藝確定的，當設計基準期內結構的維修次數分別為1次和2次時，建筑結構全過程動態可靠度水平的變化曲線分別如圖1和圖2所示。圖中縱坐標β（t）表示在t時刻結構的可靠度水平，其為無量綱物理量，橫坐標t表示結構的服役時間，其單位一般為年，也可以是天或月。β（0）表示結構在建成時的可靠度水平，然而隨著結構服役時間的延長，結構可靠度水平會因外界腐蝕環境的不同而呈現出不同的下降趨勢。其可靠度水平的下限值βmin可根據《建筑結構可靠度設計統一標準》（GB 50068-2001）確定。圖中T表示結構的設計基準期，t1、t2表示在設計基準期內，當可靠度水平下降到βmin時結構需要進行第一次及第二次維修的時間點，Δβ（t1）、Δβ（t2）則表示結構經第一次、第二次維修后可靠度水平的提升值。

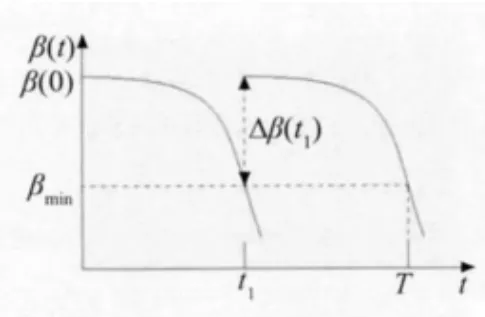
圖1 一次維修條件下的動態可靠度曲線

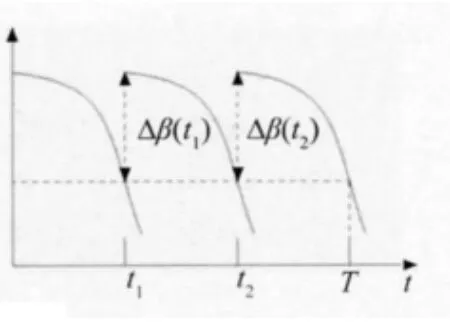
圖2 兩次維修條件下的動態可靠度曲線

由圖可知，對結構本身而言，在其設計的基準期內要求其動態可靠度水平滿足規范下限要求。圖中可靠度下限值與動態可靠度變化曲線構成的封閉圖形面積即是結構設計基準期內的安全裕度，其面積越大，則服役過程中結構的可靠度水平愈高，相應結構總投資額就越大。因此建筑結構優化目標函數（8）式的實質含義就是：結構在其設計基準期內，在滿足規范要求的前提下，安全裕度越小，越經濟。

3 受腐蝕鋼筋混凝土結構維修次數的優化

動態可靠度曲線的下降速率反映了鋼筋混凝土結構所受腐蝕的嚴重性，曲線的下降速率越大，結構所處的腐蝕環境越惡劣，所受腐蝕越嚴重［10］。若圖1、圖2中結構的設計基準期T均為50a，通過圖1與圖2對比可知，圖2中結構的可靠度曲線在單位時間內的下降速率要高于圖1，所以圖2中的結構所受到的外界腐蝕要比圖1嚴重，則圖2結構的第一次維修時間點t1要早于圖1，故選擇進行兩次維修。如果對圖2結構僅考慮一次維修，則其一次維修條件下的動態可靠度曲線如圖3所示。而如果對圖1結構考慮兩次維修，則其兩次維修條件下的動態可靠度曲線如圖4所示。

由圖3可知，對于受腐蝕影響嚴重的結構，如果僅考慮一次維修方案是顯然不合適的。同理對于受腐蝕影響較輕的結構，如果考慮兩次維修或多次維修也會產生不必要的浪費。那么如何能夠針對結構的受腐蝕情況來確定相應的維修次數就是受腐蝕結構維修次數優化的關鍵問題。

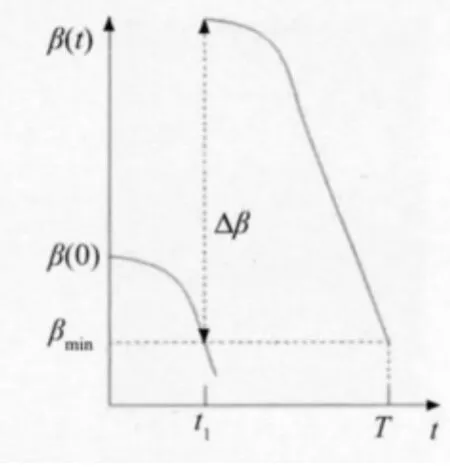
圖3 嚴重腐蝕條件下一次維修動態可靠度曲線

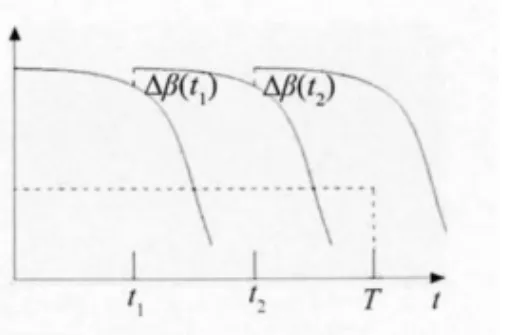
圖4 一般條件下兩次維修動態可靠度曲線

由圖1、圖2可知，在理想狀態下，當β（tn）＝βmin時，動態可靠度變化曲線與可靠度下限值構成的封閉圖形的面積達到最小，即此時最經濟。但在實際工程中大多數情況是β（tn）＞βmin或β（tn）＜βmin。由圖3、圖4可知，當β（tn）＜βmin時所產生的維修費用要遠大于β（tn）＞βmin時，所以受腐蝕結構維修次數的優化策略可表示為：

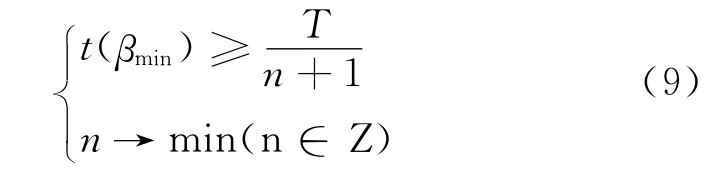
當維修次數n確定后，對維修時間點ti（i＝1，2，…，n）進行優化：

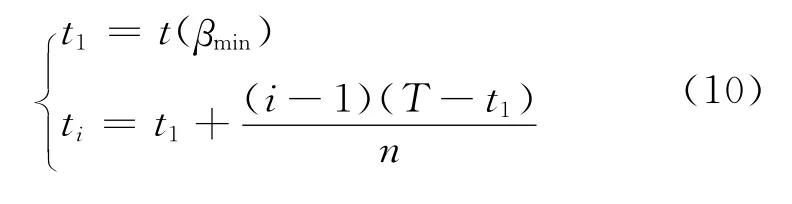
4 算例分析

在無維修條件下某鋼筋混凝土框架結構在腐蝕性介質環境中工作的動態可靠度曲線如圖5所示。試確定此結構在50a設計基準期內需進行幾次維修加固并確定各次維修的時間點。

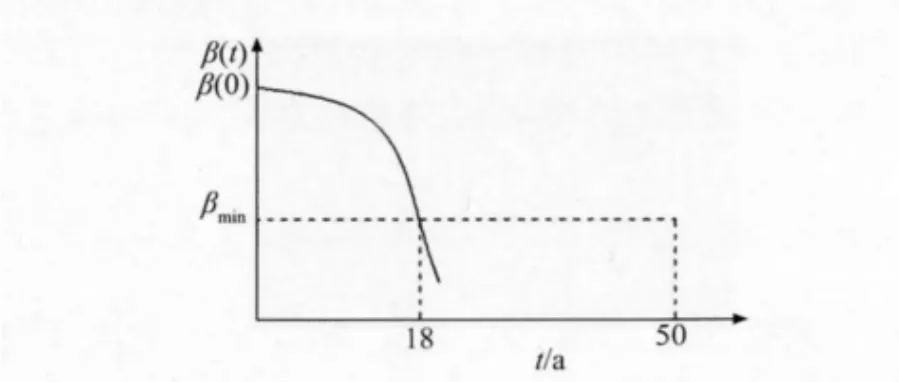
圖5 無維修條件下的動態可靠度曲線

（1）結構維修次數的優化 現假設對該結構分別進行一次、兩次和三次維修，即取n＝1，2，3代入（9）式。當n＝1時：

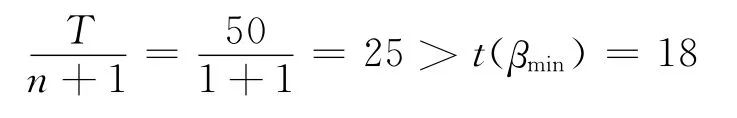
當n＝2時：

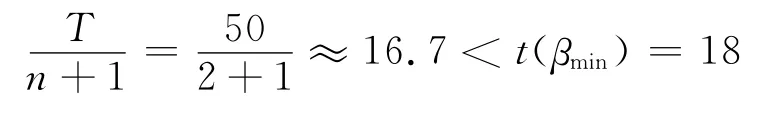
當n＝3時：

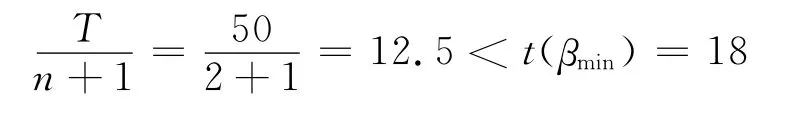
由（9）式所給條件得，即此結構在50年設計基準期內的最優維修次數為兩次。

（2）結構維修時間點的優化 由（10）式得：

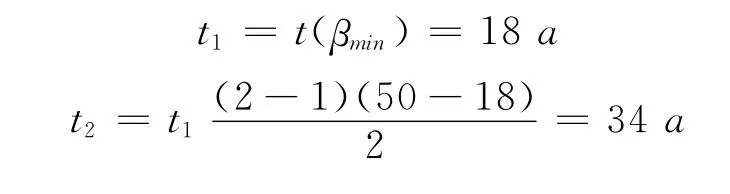
所以通過優化該受腐蝕結構應分別在服役18a和34a時進行維修。其優化后兩次維修條件下的動態可靠度曲線如圖6所示。

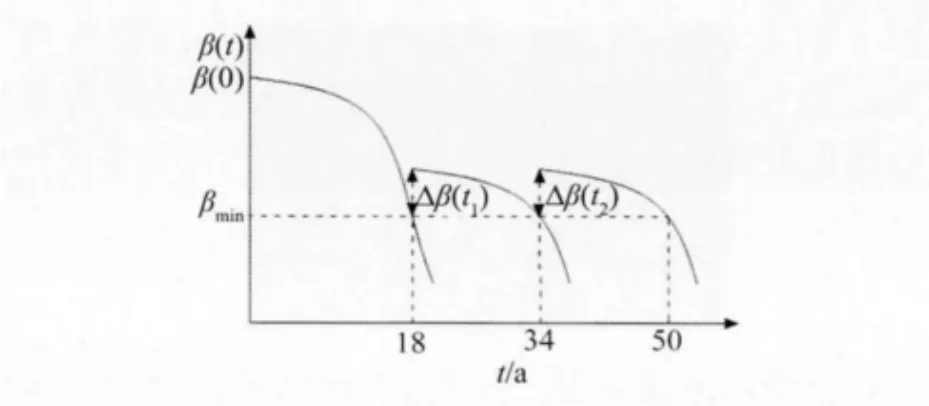
圖6 優化后兩次維修條件下的動態可靠度曲線

曲線與坐標軸所圍面積為工程總造價。將圖3與圖6對比可知，若只進行一次維修，其總造價將遠大于兩次維修。將圖4與圖6對比可知，若只簡單的將兩次維修時間點等分于設計基準期內，又會造成不必要的浪費。所以只有選擇好合理的維修次數及維修時間點，才能達到工程總造價最小的目的。

5 結論

長期處于腐蝕環境中的建筑結構，對其進行維修加固處理是使用過程中的必要環節，其設計可靠度、維修次數及維修時間點、維修可靠度水平的確定是一個復雜的全局優化問題。本工作研究了被腐蝕鋼筋混凝土結構在其服役過程中經多次維修的動態可靠度變化規律，提出了被腐蝕鋼筋混凝土結構在其設計基準期內確定最優維修次數的實用方法，并針對各維修時間點的確定進行了優化。該方法是全局規劃問題的一種定性簡化思路，對于被腐蝕嚴重且需進行多次維修加固的鋼筋混凝土結構具有一定的理論意義和實用價值。

［1］Nader M Okasha，Dan M Frangopol.Novel approach for multicriteria optimization of life-cycle preventive and essential maintenance of deteriorating structures［J］.Journal of Structural Engineering，2010，136（8）：1009-1022.

［2］Michael Macke，Shoko Higuchi.Optimizing maintenance interventions for deteriorating structures using cost-benefit criteria［J］.Journal of Structural Engineering，2007，133（7）：925-934.

［3］Mullard J A，Stewart M G.Stochastic assessment of timing and efficiency of maintenance for corroding RC structures［J］.Journal of Structural Engineering，2009，135（8）：887-895.

［4］謝桂華，李繼祥，王軍.受腐蝕混凝土結構的可靠性分析及維修決策方法［J］.四川建筑科學研究，2008，34（2）：89-92.

［5］秦劍君，劉西拉，左勇志，等.結構最優可靠度的選擇模型與經濟收益及維修策略的影響［J］.巖石力學與工程學報，2005，24（1）：97-104.

［6］郭院成，鐘維瑾，賈志堯.受腐蝕結構的動態可靠度分析［J］.鄭州工業大學學報（增刊），1999：66-69.

［7］趙國藩，金偉良，貢金鑫.結構可靠性理論［M］.北京：中國建筑工業出版社，2000.

［8］郭院成，李勐勛，趙 卓.化工結構考慮一次維修時的優化設計［J］.基建優化，2000，21（5）：1-3.

［9］郭院成，霍達，趙卓.化工鋼筋砼結構設計抗力水平的優化決策［J］.固體力學學報（專集），1999：232-235.

［10］吳謹.鋼筋混凝土結構銹蝕損傷檢測與評估［M］.北京：科學出版社，2005.