基于相互積分的應力強度因子數值分析

樂京霞 周 恒

（武漢理工大學交通學院 武漢 430063）

0 引 言

80%以上的結構嚴重破壞是由于疲勞和斷裂破壞引起的［1］．對于斷裂問題，常采用應力強度因子（stress intensity factor，SIF）這一物理量來反映裂紋尖端彈性應力場的強弱．傳統求解SIF方法很多，如應力函數法、積分變換法、有限單元法、邊界元法和邊界配置法等．以上方法理論成熟，但需要繁瑣的推導和計算．文獻［2］給出了部分簡單裂紋模型的SIF計算公式．然而真實構件中的裂紋形態分布各異，手冊不可能完全覆蓋．因此，利用商用有限元分析軟件對裂紋尖端應力場進行數值模擬進而計算SIF的方法，由于其簡便易行，逐漸成為工程中解決疲勞斷裂問題常用方法．

ANSYS求解斷裂力學問題的步驟為：首先進行線彈性分析或彈塑性靜力分析，然后用特殊的后處理命令、或宏命令計算所需的斷裂參數．其自帶的KCALC命令可直接由裂尖應力／位移場插值求解出SIF．在新推出的高版本ANSYS中增加了一種基于相互積分理論的數值計算命令CINT．本文利用ANSYS有限元分析軟件，基于上述兩種不同的斷裂力學理論模型，分別求解了張開型二維裂紋及三維裂紋的SIF值，并將數值計算結果與理論解析解和裂紋擴展實驗結果進行比較，得出了更為準確的張開型裂紋應力強度因子數值計算方法．

1 基于相互積分法理論的應力強度因子計算

相互作用積分法假定含裂紋彈性介質受到2個載荷的共同作用：有單獨真實載荷引起的裂紋尖端力學場，稱為真實應力σki，σkj；uk，i為真實場中的位移；σauxkj稱 為 輔 助 場 的應力；uauxk，i為 輔 助場中的位移；qi，j為裂紋擴展矢量；qn為裂紋擴展法向；δi，j為克羅次符號［3］．將 真實場 和輔助 場疊加代入J積分，再分離出由真實場和輔助場分別引起的J積分，剩余的真實場和輔助場相互作用項即為相互作用積分I，其表達式為

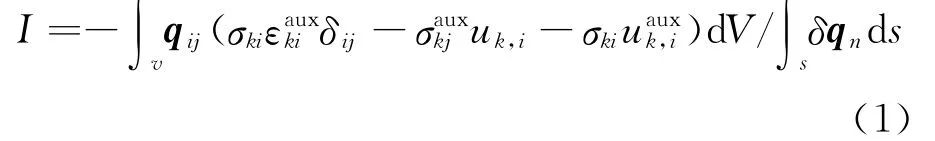
相互作用積分I和應力強度因子相關聯的定義式為

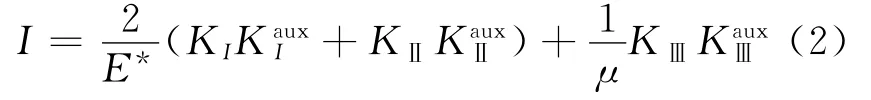
式中：Kaux分別為輔助場中的應力強度因子；E＊為平面應力和平面應變下的彈性模量；μ為剪切模量．

2 二維裂紋應力強度因子數值分析

2．1 基于ANSYS的數值模擬

數值模擬實驗的對象為對邊受拉應力σ的中心裂紋板，板的高度、寬度和厚度分別為2 H，2W和B，中心裂紋的總長為2a．假設板的材料各向同性、均勻、線彈性，其彈性模量和泊松比分別是E＝2×105MPa和ν＝0．25［4］．數值模擬根據受力不同和試樣幾何尺寸不同總共進行了6次，表1給出的是不同的實驗模型的具體參數．利用模型的對稱性，取模型的1／4進行分析，見圖1．在裂紋尖端第一排的單元要有奇異性，采用平面單元（PLANE183）進行網格劃分，各個模型的網格尺寸相同，方便計算結果的對比．采用Plane strs w／thk，不考慮厚度方向的影響，簡化為平面應力模型．模型左邊所有的節點X方向以及下面裂紋尖端以右的所有節點的Y方向進行約束，對模型的所有的上邊緣進行加載．

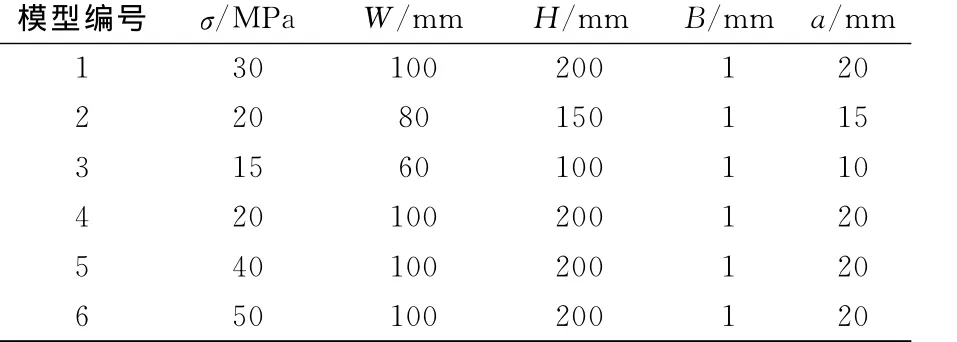
表1 數值模擬所選取的模型

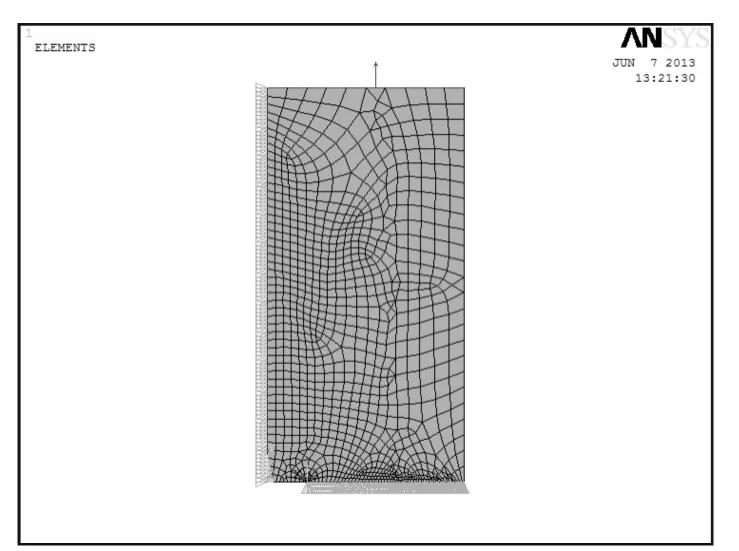
圖1 中心裂紋板有限元模型

針對上述中心裂紋板模型，利用ANSYS軟件進行有限元分析，圖2給出了裂尖區域應力云圖．然后分別采用位移插值法和相互積分法，計算得出各個模型的應力強度因子．高版本ANSYS提供的CINT命令可基于相互積分法求出SIF，本文考慮裂尖奇異性和應力集中等影響，取第二圈和第三圈單元積分值的算術平均作為最終SIF．

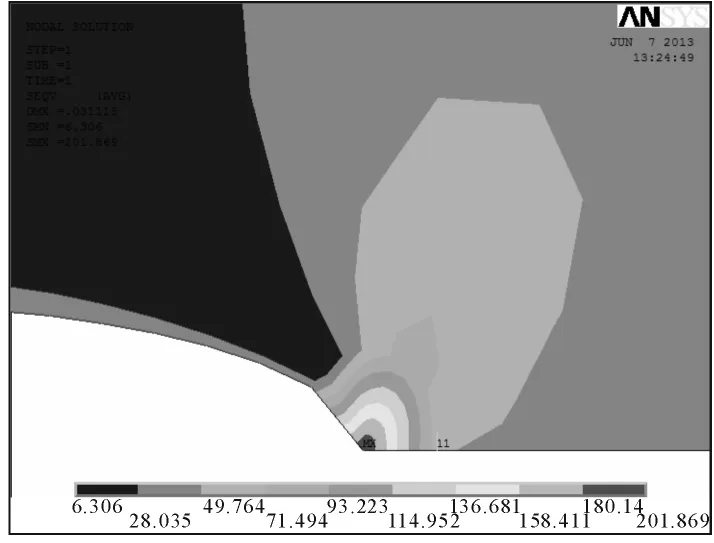
圖2 裂尖區域von－Mises應力云圖

2．2 與線彈性斷裂力學解析解的對比分析

對于無限遠受拉中心裂紋板問題，其應力強度因子已經有理論解，參看下式．

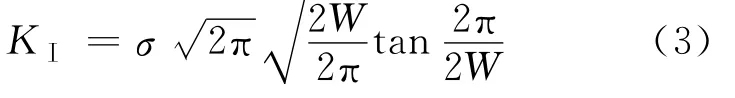
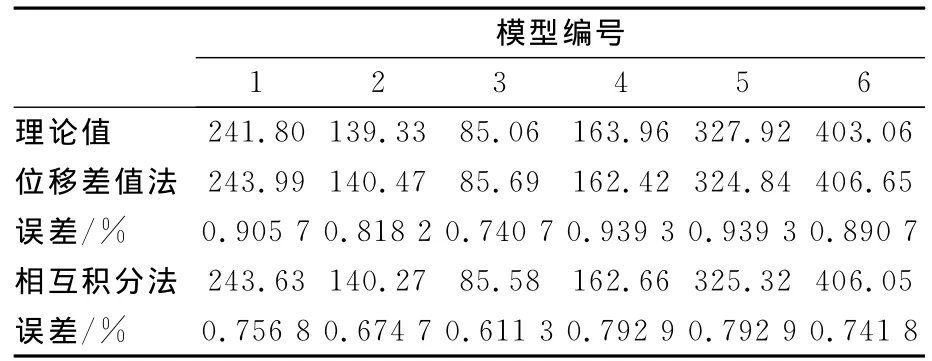
表2 應力強度因子的數值分析結果與理論解比較／應力強度因子

由表2可見，數值分析結果和理論解的誤差不超過1%，且模型載荷與裂尖應力強度因子的線性關系［5］，驗證了 ANSYS求解張開型裂紋SIF的可靠性．其中，基于相互積分的數值計算對網格精度要求低，計算更為簡便．

3 三維裂紋應力強度因子數值分析

3．1 應力強度因子的測量實驗

本文根據國標GB／T 6398—2000，通過裂紋擴展速率測試實驗推算出三維裂紋的應力強度因子，計算公式如下［6］．

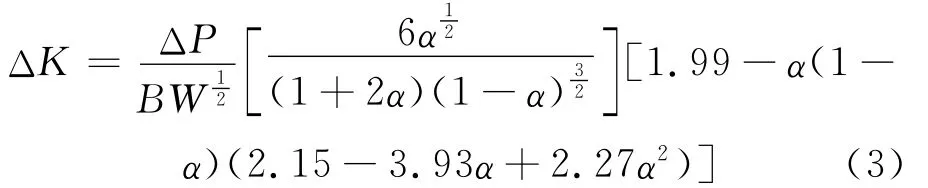
式中：ΔK是應力強度因子幅值；α＝2a／W．

所用試件類型為標準的單邊缺口三點彎曲試件．厚度方向B＝36mm，試件高度W＝75mm，試件跨距S≈4B＝300mm，預制初始疲勞裂紋長度為9mm．加載裝置為JXG－200高頻疲勞試驗機，材料為Q370qE高強度鋼板母材．實驗載荷最大值Pmax＝35kN，最小值Pmin＝3．5kN，載荷比為R＝0．1，載荷幅值為ΔP＝31．5kN．

3．2 基于ANSYS的數值模擬

對于上述實驗模型，采用ANSYS的SOLID186體單元，沿試件厚度B方向劃分3層網格進行有限元計算．試件所受載荷幅值為31．5kN，假定兩端分別約束X，Y，Z方向和X，Z方向的位移．采用彈性模量E＝2×105MPa和泊松比ν＝0．3進行計算．分別采用位移插值法和相互積分法，計算得出各個模型的應力強度因子．計算結果和實驗結果的比較見表3．

表3 應力強度因子幅值的數值分析結果和實驗值比較 MPa·m1／2

表3中列出的是試件表面Z＝75mm處的計算結果．從以上的計算中可以看出，位移差值法求取的ΔK不超過3%，而相互積分法計算誤差比前者小一個數量級，更接近與實驗測量值．另外，在采用位移插值法求解SIF時，沿著裂尖厚度方向每次只能計算出一個值，需要輸入裂紋前緣不同的位置坐標才能計算出不同位置的SIF．但是，相互積分法只需要一次后處理，就可以輸出沿著裂紋厚度方向SIF的系列值，更加適用于三維裂紋的數值分析．

4 結束語

文中對二維及三維張開型裂紋應力強度因子數值分析方法研究，并將數值計算結果同線彈性斷裂力學解析解和疲勞裂紋擴展實驗實測值進行了對比分析，得出如下結論：對于二維裂紋，位移差值法和相互積分法和理論值的誤差均不大于1%；對于三維裂紋，采用相互積分法求取的應力強度因子的誤差比位移差值法的計算結果小一個數量級．鑒于相互積分法只需要一次后處理，就可以輸出沿著裂紋厚度方向應力強度因子的分布，為三維裂紋擴展的數值模擬提供了參考．本文只對靜載荷和I型裂紋進行了模擬，今后，還可對動態載荷和復合型裂紋擴展進行更進一步的探索．

［1］崔維成，蔡新剛，冷建興．船舶結構疲勞強度校核研究現狀及我國的進展［J］．船舶力學，1998（4）：63－81．

［2］仇仲翼．應力強度因子手冊［M］．北京：科學出版社，1993．

［3］于紅軍．含復雜界面非均勻材料斷裂力學研究［D］．哈爾濱：哈爾濱工業大學，2010．

［4］解 德，錢 勤，李長安．斷裂力學中的數值計算方法及工程應用［M］．北京：科學出版社，2009．

［5］張曉敏．斷裂力學［M］．北京：清華大學出版社，2012．

［6］國家質量技術監督局．GB／T 6398—2000金屬材料疲勞裂紋擴展速率試驗方法［S］．北京：中國標準出版社，2000．