U型結構在鐵路路堤地段的應用研究

吳劍鋒，李季宏

(鐵道第三勘察設計院集團有限公司，天津 300251)

1 概述

U型結構作為一種輕型支擋結構，由于其剛度大、變形小、穩定性好、收坡防水支擋效果明顯，在許多鐵路工程建設中，特別是在地下水豐富、水位較高、放坡受到限制的挖方路基地段，愈來愈顯示其獨特的適應性。丁兆鋒[1]對U型槽設計中的理論計算及結構施工圖等關鍵技術問題進行了探討，孫愛斌[2]根據天津某公鐵立交工程中道路以下鉆方式通過地下水路塹的特點，對封閉式路塹U型槽結構的設計與計算進行研究。

但當前的理論研究及應用主要集中在挖方路基U型槽這一部分，對路堤地段U型結構這一部分的研究及應用還很少，結合某鐵路工程的工程實踐，對路堤地段U型結構的設計及應用進行了研究。

2 U型結構形式

U型結構主要由鋼筋混凝土邊墻與底板組成，結構內填筑路基填料，邊墻內側面設置一層砂夾卵石反濾層，基床表層上部鋪設不透水土工布防止雨水下滲，雨水流入滲水暗溝，并通過PVC排水管將暗溝水引到槽外，并在邊墻與底板上按一定距離設置泄水孔排水；暗溝上設電纜槽，墻頂設置欄桿。U型結構半斷面構造示意如圖1所示。

圖1 U型結構半斷面構造示意

3 結構設計

3.1 計算模型

U型結構受力主要包括：結構自重、列車活載、邊墻土壓力、水平地震力、地基反力。列車活載按換算土柱計算。

按照U型結構的受力特點，可取線路方向一延米按彈性理論進行簡化計算，簡化計算模型如圖2所示。U型結構邊墻按懸臂構件計算，底板按照彈性地基梁考慮。彈性地基梁采用Winkler模型計算

Pi=K0Si(1)

式中Pi——地基任一點所受的壓力強度，kN/m2；

K0——基礎系數，kN/m3；

Si——地基任一點的沉降值，m。

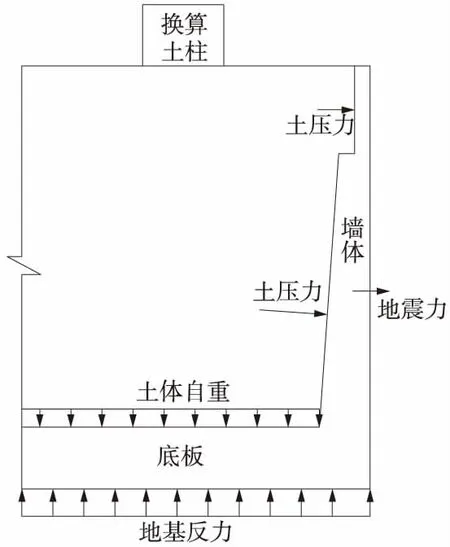
圖2 U型結構計算模型示意

3.2 土壓力計算

剛性墻體的位移模式包括平移(T)、繞墻底轉動(RB)及繞墻頂轉動(RT)等3種基本位移模式。U型結構邊墻作為懸臂構件，在土壓力作用下，將繞墻底向外轉動，故屬于RB位移模式。RB位移模式下，隨著轉角增大，墻后土體塑性區呈條帶狀逐漸向下發展，達到極限主動狀態時，形成的滑動破裂面與庫侖滑動面一致，滑動面內土體均處于塑性狀態，墻高內各點土體從上到下依次達到主動狀態[3]。Sherif[4]等通過模型試驗認為墻高內各點土體達到主動狀態所需的水平位移Sc為定值，約為0.000 3H～0.000 5H(H為墻高)。U型結構為鋼筋混凝土構件，剛度大，墻體位移一般小于Sc，計算時參照《鐵路路基支擋結構設計規范》相關規定，按主動土壓力考慮，同時附加安全系數1.1～1.3。

U型結構抗震設計需考慮地震土壓力。目前，實際工程中應用最廣泛的方法是基于極限平衡理論的Mononobe-Okabe理論。Mononobe-Okabe理論是在庫侖土壓力的基礎上，考慮地震慣性力后建立的地震土壓力合力計算公式。假設作用于墻背上的地震土壓力是由墻后填土在極限平衡狀態下出現的滑動楔體產生，該滑動楔體為剛體，在地震作用下具有相同的加速度。由作用于該滑動楔體上力的平衡條件，可得到作用于墻背上的地震土壓力合力PAE

(2)

KAE=

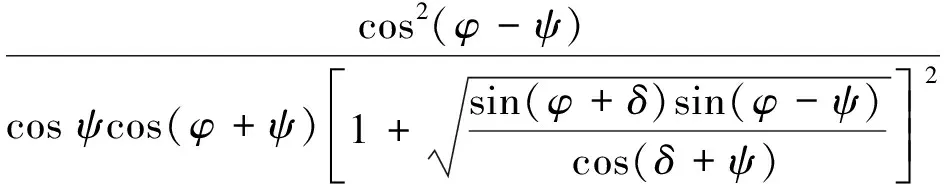
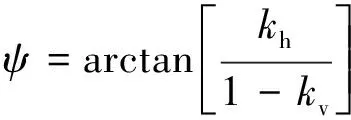
式中KAE——地基主動土壓力系數；

φ——墻后土體內摩擦角，(°)；

δ——墻后土體與墻背之間的摩擦角，(°)；

ψ——地震角，(°)；

kh——水平地震加速度與重力加速度的比值；

kv——豎向地震加速度與重力加速度的比值。

3.3 結構內力

根據結構力學計算方法，可得U型結構的彎矩圖，如圖3所示。由圖3可知，邊墻內側受拉，墻懸臂段底部B節點彎矩最大，彎矩值隨著墻高增加而增大；底板除邊墻位置處承受正彎矩外，其余部分均為負彎矩，且負彎矩值遠遠大于正彎矩值，底板彎矩值隨著墻高的增加與地基系數的降低而增大。A節點為墻截面尺寸變化點，墻截面尺寸小，故A、B節點處為墻截面控制截面，且易出現應力集中現象，是U型結構設計的重點，應采取加密箍筋等構造措施。底板的控制截面為跨中C處與底板固結段根部D處，此兩處的負彎矩最大。

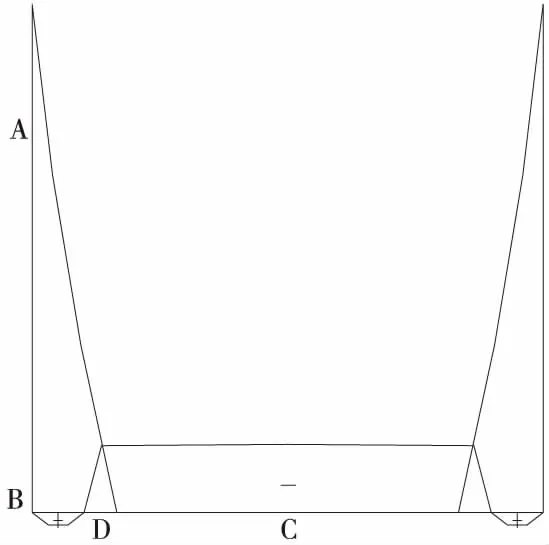
圖3 U型結構彎矩示意

4 計算實例

某雙線鐵路，標準線間距4 m，設計速度160 km/h，地震峰值加速度0.4g。線路位于平原區，均為填方段落，由于征地條件限制，擬采用鋼筋混凝土U型結構收坡，本工程雙線地段主體結構用地僅為9 m，收坡效果明顯。現以該鐵路DK140+050～DK140+250段落為工程實例，進行計算分析。該段落墻高7 m，地層如下：雜填土，黃褐色、稍密、潮濕、厚0.0～1.5 m；黏土，灰褐色，軟塑～硬塑，厚2.2～3.2 m；淤泥，灰褐色，流塑，厚4.6～6.1 m；粉砂，褐灰色，中密，飽和。

經計算，最不利荷載組合下，邊墻B點彎矩值MB=799 kN·m，邊墻根部D處D點彎矩值MD=816 kN·m。底板橫向寬度范圍內彎矩值如圖4所示。

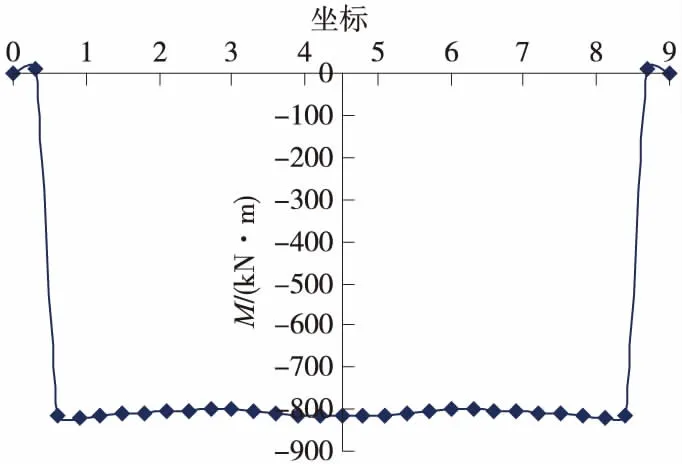
圖4 底板彎矩示意

U型結構邊墻和底板按照受彎構件單筋梁[6]計算，強度計算公式為

(5)

主筋截面面積計算公式為

As=α1fcbx/fy(6)

式中α1——系數，混凝土強度等級不超過C50時，取1.0；

fc——混凝土軸心抗壓強度設計值，N/mm2；

活佛把醫學和佛經結合起來，給我們講《四部醫典》。他告誡我們，對待病人就像對待母親一樣竭盡全力。即便是半夜出診，也不能心有怨言，更不可看重錢財。活佛教育我們，行醫時不能隨便增加醫藥費。病人因此耽誤病情，就等于謀財害命。真誠的話語就像太陽一樣溫暖人心。治療中好言好語容易做到，傾聽病人的感受則不太容易做到。一個好曼巴應該把病人當作家人朋友那樣說話。[注]訪談人：歐陽麗婷；訪談對象：久麥多杰；訪談時間：2015年9月28日；訪談地點：青海省興海縣莫多寺。

b——矩形截面寬度，m；

x——混凝土受壓區高度，m；

h0——截面有效高度，m；

fy——鋼筋抗拉強度設計值，N/mm2。

裂縫控制驗算公式為

(7)

式中αcr——構件受力特征系數；

ψ——裂縫間縱向受拉鋼筋應變不均勻系數；

σsk——按荷載效應的標準組合計算的鋼混構件縱向受拉鋼筋的應力，N/mm2；

Es——鋼筋彈性模量，N/mm2；

c——最外層縱向受拉鋼筋外邊緣至受拉區底邊的距離，mm；

deq——受拉區縱向鋼筋的等效直徑，mm；

ρte——按有效受拉混凝土截面面積計算的縱向受拉鋼筋配筋率。

經分析計算，邊墻所需的主筋面積為3 848 mm2，選用6φ20+4φ25，配置在墻內側；底板所需的主筋面積為4 378 mm2，選用3φ20+7φ25，配置在板上緣。箍筋與構造筋均按構造規定選用。

5 結論及建議

(1)U型結構在路堤地段具有良好的收坡效果，節省用地。

(2)U型結構計算時應考慮結構自重、列車活載、邊墻土壓力、水平地震力等荷載，考慮多種荷載的組合情況，按最不利荷載組合設計。

(3)土壓力計算可采用各種邊界條件下的庫侖主動土壓力進行計算，并考慮地震作用對土壓力的影響。

(4)U型結構設計可按單筋受彎構件計算，邊墻控制截面位于邊墻截面變化處與邊墻懸臂段根部；底板控制截面位于跨中截面與底板固結段根部處，且底板彎矩值隨著墻高的增加與地基系數的降低而增大。

(5)本文僅對路堤地段U型結構結構設計方面進行了闡述，未涉及到地基處理、排水設計、與接觸網支柱接口等系統設計，應作進一步研究。

[1] 丁兆鋒，吳沛沛.U型槽結構設計與分析[J].鐵道工程學報，2009，127(4)：13-16.

[2] 孫愛斌，吳連海.天津某封閉式路塹U型槽結構的設計與計算[J].鐵道工程學報，2006，97(7)：49-53．

[3] 龔慈.不同位移模式下剛性擋土墻土壓力計算方法研究[D].杭州：浙江大學，2005：31-34．

[4] Sherif M A， Fang Y S， Sherif R I.KAandK0behind rotating and non-yielding walls[J]. Journal of Geotechnical Engineering， 1984，110 (1)：41-56．

[5] 李毓林.鐵路路基手冊[M].北京：中國鐵道出版社，1992：346-351.

[6] 舒士霖.鋼筋混凝土結構[M].杭州：浙江大學出版社，2002：89-90．