透鏡的等光程性問題

王家慧 何志巍 金仲輝

(中國農業大學應用物理系 北京 100083)

在講授等傾干涉和夫瑯禾費衍射時，都要涉及透鏡光程性的問題．我們先來看看不同的物理教材是如何闡述這個問題的．

文獻[1]中是這樣敘述的，平行光束通過透鏡后，將會聚于焦平面上成一亮點F(圖1)．這是由于某時刻平行光束波前上各點(圖1中A,B,C,D,E各點)的相位相同，而到達焦平面后相位仍然相同，因而干涉加強．可見,這些點到F的光程都相等．

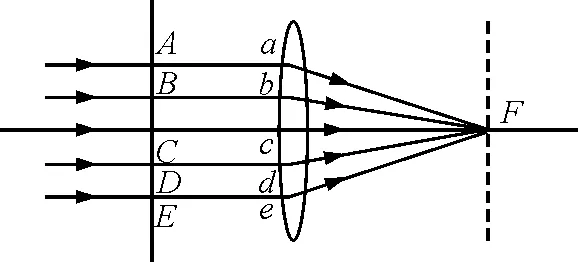
圖1

文獻[2]是這樣敘述的，平行光通過透鏡后，各光線要會聚在焦點，形成一亮點，這一事實說明，在焦點處各光線是同相的．

上述兩種教材對透鏡等光程的敘述基本上是相同的，但是從敘述的邏輯上來看，后者更恰當些，即從實驗結果(即像點是亮點)來看，可以推斷出，所有成像的光線是同相的，即所有成像的光線光程相同．相干疊加得到加強才得到亮點．而前者的敘述在邏輯上多少有些混亂，將因果關系顛倒了．

圖2

關于透鏡的等光程性還可用費馬原理來論證．費馬原理的表述為，空間Q，P兩點間光線的實際路徑是光程(QP)為極小值或極大值或恒定值的路徑．圖2中從物點S向透鏡發出再從透鏡射出會聚于S′的一束光是連續分布的，也就是說，從物點S到像點S′實際上有無窮多條光線路徑．根據費馬原理，它們的光程都應取極值或恒定值．這些連續分布的實際光線都取極小值或極大值是不可能的，唯一的可能性是取恒定值，即它們的光程都相等．

還有些教材對透鏡等光程性的論證是有缺陷的，例如，“正入射的平行光會聚于焦平面上F點(圖1)，雖然邊緣光線(如AaF)比中部光線(如CcF)經過的幾何路程長，但前者在透鏡中的路程比后者的短，考慮到透鏡的折射率大于1，可認為兩光線經過透鏡后光程的變化相等．”從以上敘述內容來看，顯然并沒有論證這兩條光線的光程是相等的，而僅僅是一種推想而已．

另一本教材對透鏡等光程性是這樣描述的，“經過透鏡邊緣與透鏡中心附近光線的幾何路程是不同的，例如CcF的幾何路程比AaF短(圖1)，但前者在透鏡中的路程比后者長，而透鏡材料的折射率大于1，如果折算成光程，通過計算可以證明兩者的光程相等，使用透鏡不會改變光程差．”從以上敘述內容來看，作者沒有給出簡明的方法來論證透鏡的等光程性，如果學生問我們如何來計算？恐怕不是簡單幾句話就可以說明白.

由以上的討論可以知道，教師在備課過程中需要閱讀不同的教材，認真分析和比較它們的不同之處，從中挑選一種比較正確的敘述方法．

參考文獻

1 馬文蔚.物理學(下冊).北京：高等教育出版社，2006.117

2 張三慧. 大學物理學(第2版)(第四冊). 北京：清華大學出版社，2000.139