淺談泥水平衡機(jī)械頂管施工技術(shù)
王晨旭 吳奇飛 郭耀龍
摘 ? ?要:泥水平衡機(jī)械頂管技術(shù)是一種比較成熟的應(yīng)用范圍較廣的非開槽施工技術(shù),為了更好地介紹泥水平衡機(jī)械頂管技術(shù),簡要地介紹泥水平衡機(jī)械頂管的關(guān)鍵措施,并提出管材加強(qiáng)等優(yōu)化,提高泥水平衡機(jī)械頂管技術(shù)實際施工中的效率。
關(guān)鍵詞:泥水平衡機(jī)械頂管;關(guān)鍵措施;優(yōu)化;總結(jié)
1 ?前言
泥水平衡機(jī)械頂管技術(shù)是一種非開槽施工技術(shù),目前已經(jīng)在城市地下管網(wǎng)工程中得到了大范圍的使用,該技術(shù)具有適用范圍廣、挖掘面穩(wěn)定、地面沉降少等優(yōu)點。現(xiàn)階段我國關(guān)于泥水平衡頂管的應(yīng)用仍處于經(jīng)驗性階段,很多實際的施工憑借經(jīng)驗施工,通過對實際工程施工經(jīng)驗的研究和總結(jié),可以改善該類工程的施工現(xiàn)狀,更好地指導(dǎo)該類工程的施工。
2 ?工程概況
商丘市污水管網(wǎng)和中水管網(wǎng)工程含12條污水管網(wǎng),全長42km。其中36km污水管網(wǎng)全部采用泥水平衡機(jī)械頂管施工,采用鋼筋混凝土沉井作為工作井與接收井,管材為“F”型Ⅲ級鋼筋混凝土鋼承口管,管徑為800mm~2000mm不等,管道埋深為5m~10m不等。
3 ?頂管施工關(guān)鍵措施
3.1 ?前期地形地質(zhì)調(diào)查
作為暗挖工程,前期的地形地質(zhì)調(diào)查尤為重要,在認(rèn)真研讀勘查報告的基礎(chǔ)上,泥水平衡機(jī)械頂管施工主要對以下幾方面進(jìn)行調(diào)查:
(1)對頂進(jìn)路線上方的建筑物及建筑物地基基礎(chǔ)進(jìn)行調(diào)查;(2)對沉井及頂進(jìn)路線的管線或臨近管線(具體位置、標(biāo)高、管道材料、管徑、權(quán)屬單位)、構(gòu)筑物(具體位置、構(gòu)筑物標(biāo)高、結(jié)構(gòu)形式),湖泊河流(具體水位及河床湖泊底部的標(biāo)高)、垃圾填埋場(填埋區(qū)域、深度)、建筑垃圾填埋區(qū)(填埋區(qū)域、深度)、下穿道路進(jìn)行統(tǒng)計;(3)對沉井施工區(qū)域上空架設(shè)的電線、電纜等其他障礙物進(jìn)行調(diào)查;(4)對進(jìn)場道路進(jìn)行調(diào)查;對主要施工交通路口、人行道出口等進(jìn)行調(diào)查;(5)互聯(lián)互通管線位置及管內(nèi)底標(biāo)高核查。
3.2 ?觸變泥漿減阻措施
當(dāng)機(jī)頭全部進(jìn)入封閉后,開始由機(jī)頭向管外壁注觸變泥漿,使管外壁形成泥漿套,起到減阻、潤滑作用。
(1)注漿孔設(shè)置。頂管機(jī)尾部設(shè)置一節(jié)注漿特殊管,管內(nèi)設(shè)置三道注漿孔,每道斷面上布置5個注漿孔,孔相互交錯,確保漿液能均勻分布,形成完整有效的觸變泥漿套。布漿與補(bǔ)漿采用同一根主管,注漿孔設(shè)置在靠近承口鋼套環(huán)覆蓋的位置,每一組注漿孔有3個,分別設(shè)置在混凝土管的腰部和頂部。通常在機(jī)頭后的1~3節(jié)管分別設(shè)置一組布漿孔,尤其注意第一節(jié)管道的布漿應(yīng)現(xiàn)先布后頂,使機(jī)頭漿套完整,從而完美進(jìn)洞。補(bǔ)漿孔按一定規(guī)律每3~8管節(jié)(按每節(jié)管道長2m考慮)應(yīng)設(shè)置一組
(2)注漿方法。注漿原則:先壓后頂,隨頂隨壓,隨頂隨補(bǔ),頻繁小量補(bǔ)漿。注漿應(yīng)由專人負(fù)責(zé)。注漿以頂管工具管后4~5節(jié)為主,注入漿液形成漿套。頂前4~5節(jié)管時球閥始終開著,頂進(jìn)距離超過100m后,注漿不允許停。從洞口位置往機(jī)頭方向逐一補(bǔ)漿,補(bǔ)至機(jī)頭后側(cè)后,重復(fù)向洞口位置補(bǔ)漿,每次管道頂進(jìn)中對每組補(bǔ)漿孔補(bǔ)漿,但每組補(bǔ)漿時間短,一般為2分鐘以內(nèi),頂管越長補(bǔ)漿時間越短。此補(bǔ)漿措施大大減小了頂進(jìn)過程中的摩阻力。正常施工中減阻泥漿的施工控制較好時,一般會遠(yuǎn)小于規(guī)范的計算值;因此大面積施工前可進(jìn)行試驗段,調(diào)整注漿量、注漿壓力、注漿方式以達(dá)到較好的減阻效果。并且可據(jù)此估算不加設(shè)中繼間情況下管道最大頂進(jìn)長度,確定每段頂進(jìn)中繼間的使用數(shù)量。
3.3 ?管材加固措施
在實際泥水平衡頂管施工過程中由于各種原因管材會出現(xiàn)破壞,現(xiàn)通過現(xiàn)場試驗和Midas數(shù)值模擬分析,對管材的受力性能進(jìn)行了一定的研究,對頂進(jìn)過程中的受力和變形進(jìn)行研究,發(fā)現(xiàn)管材主要發(fā)生破壞的原因是由于管材的插口和承口處發(fā)生應(yīng)力集中現(xiàn)象,從而局部應(yīng)力超過混凝土強(qiáng)度,發(fā)生破壞。其次是由于在頂進(jìn)過程中管材在土壓力和頂力的共同作用下發(fā)生破壞。針對這兩種破壞形式,分別在插口和承口區(qū)域通過加設(shè)鋼拱架進(jìn)行補(bǔ)強(qiáng)、采用更厚的環(huán)鐵減小管材的局部承壓區(qū)和通過U型鋼筋加強(qiáng)鋼筋骨架的方式,對管材進(jìn)行一定的優(yōu)化設(shè)計,從而更好地符合實際施工的需求。
3.4 ?進(jìn)出洞口措施
在頂進(jìn)施工中,進(jìn)出洞口的成敗決定了整個工程的成功與否。進(jìn)出洞口的順利施工主要從洞口加固和洞口止水兩個角度來考慮。在頂進(jìn)軸線的進(jìn)出洞口位置5m范圍內(nèi)進(jìn)行注漿加固,保證在進(jìn)出洞口范圍內(nèi)土質(zhì)的穩(wěn)定,防止地層發(fā)生坍塌,影響洞口的穩(wěn)定性,這是保證進(jìn)出洞口安全最有效的措施。另一措施則是止水裝置,采用預(yù)埋螺栓、鋼壓環(huán)及橡膠圈共同組成的止水裝置,可以有效防止施工過程中的水、土流失,影響洞口范圍內(nèi)土層的穩(wěn)定性,這是保證泥漿套形成的重要措施。
3.5 ?測量與糾偏措施
頂管施工應(yīng)針對每段頂管建立獨立的控制網(wǎng)絡(luò),直線頂管過程中測量可采用激光經(jīng)緯儀,曲線頂管除采用管內(nèi)支導(dǎo)線人工測量外,目前應(yīng)用較廣的為自動測量系統(tǒng)。施工前應(yīng)對測量儀器進(jìn)行檢查校驗,過程中應(yīng)對控制樁進(jìn)行復(fù)核,采用激光經(jīng)緯儀測量時,每班組交接工作時,應(yīng)重新進(jìn)行方向校核。頂管糾偏必須堅持勤測微糾少糾,在頂管頂進(jìn)過程中要不斷與設(shè)計軸線相比較,發(fā)現(xiàn)偏差及時糾正,糾偏角度在10~20之間,不得大于1度。糾偏應(yīng)在在管道頂進(jìn)過程中進(jìn)行,避免靜止?fàn)顟B(tài)糾偏。
3.6 ?障礙物處理措施
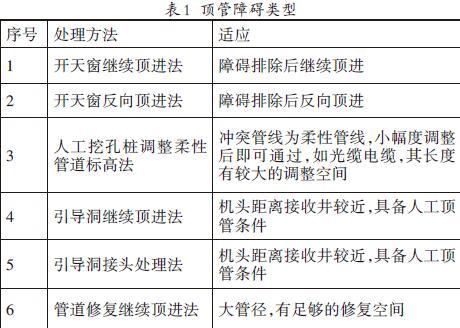
作為一種典型的非開槽施工技術(shù),面對復(fù)雜多變的地下施工條件,頂管遇障成為頂管施工必須要面對的一個問題,頂管遇障的原因不同也就造成了處理方式的不同,目前常見的頂管遇障措施主要分為以下幾種。
雖然目前很難提供經(jīng)濟(jì)而又實用的方式完全避免頂管遇障,但是針對不同的情況,快速、準(zhǔn)確地提供切實有效的處理方式,不讓頂管遇障成為施工中不可處理的難題,拖延工程進(jìn)度,影響工程質(zhì)量,這是目前該類問題的另一出路。
4 ?結(jié)束語
泥水平衡法頂管施工的技術(shù)體系目前已經(jīng)較為完善,但因其受地形地質(zhì)、地上及地下障礙物等多方面因素的影響,施工人員必須因地制宜,不斷總結(jié)經(jīng)驗,進(jìn)行動態(tài)施工管理,注重過程技術(shù)問題處理,以提高了施工的安全性,從而保障了工程的效益。
參考文獻(xiàn):
[1] 葛春輝.頂管工程設(shè)計與施工[M].北京:中國建筑工業(yè)出版社,2012.
[2] 武志國,陳勇,王兆銓.頂管技術(shù)規(guī)程[M].北京:中國建筑工業(yè)出版社,2016.
[3] 張明媚.淺析泥水平衡法頂管施工技術(shù)[J].科技經(jīng)濟(jì)市場,2006(12):66+74.

