西洞庭湖區杉木林分相對樹高曲線模型的研究

孫擁康，李際平，呂 勇

（中南林業科技大學 林學院，湖南 長沙 410004）

西洞庭湖區杉木林分相對樹高曲線模型的研究

孫擁康，李際平，呂 勇

（中南林業科技大學 林學院，湖南 長沙 410004）

為了在森林資源調查中能夠方便快捷地估測出具有較高精度的林分蓄積量，以西洞庭湖區96塊林分樣地資料為基礎，建立該區杉木林分相對樹高曲線模型。經假設檢驗（t檢驗）得該模型估計精度較理想，可達到近似實測樹高曲線法的水平，既避免了較大地域范圍因形高變異而引起估測立木材積的較大偏差問題，又降低了實際工作中的技術難度和工作量。

西洞庭湖區；杉木；相對樹高曲線模型；假設檢驗

蓄積量是衡量森林產量、森林生產力、森林多種效益的重要指標[1]。有效減小估測誤差，并獲得較高精度的林分蓄積量，對森林資源科學經營管理及合理開發利用，確定采伐限額和伐區設計，滿足森林資源資產評估需要，促進林業生產等都具有重要的實際意義。

由于同樹種相同胸徑的立木在較大的地域范圍其形高變異較大，使估測的立木材積與真實材積存在較大的偏差，這對于森林采伐限額的控制、林木資產的評估與管理都極為不利[2]。如果利用二元材積表估測立木材積，固然可以提高估測的精度，但內業工作繁瑣，大大增加了實際工作中的技術難度和工作量。在此背景下，駱期邦等[3]通過研究提出建立相對樹高曲線模型，進而獲得具有較高精度林分蓄積的方法，并得到較好的應用推廣；謝哲根等[4]在此基礎上，對林分徑階蓄積量與材種出材量測算進行了方法上的改進研究，并獲得了較高的估測效果；曾偉生等[5-7]也結合相對樹高曲線模型，分別對天然林直徑分布規律、胸徑與冠幅相關性、出材率表編制等進行了有益的研究和探索。但是，由于受地理區域的限制，研建模型的結果常缺乏廣泛的代表性。因此，筆者以湖南省常德市西洞庭湖區域杉木林分為研究對象，設置不同行政區域不同立地條件下杉木林分臨時標準地，并結合該區森林資源二類調查資料，建立其相對樹高曲線模型，以期為該區杉木林分立木材積的估算提供一種快捷而精確地方法。

1 材料與方法

1.1 研究區概況

西洞庭湖區位于湖南省常德市、洞庭湖西部，地勢上處于云貴高原、湘西山地向洞庭湖平原過渡的交接地帶，屬中亞熱帶季風氣候，氣候溫和濕潤、四季分明。西洞庭湖區植被豐富，產量大，蘊藏量高，既是重要的用材林生產基地，又是區域社會經濟發展的重要經濟來源。區域林區總面積為444 100.22hm2，其中杉木類面積為45 090.7 hm2，占總面積的10.14%。

1.2 相對樹高曲線法的基本原理

1.2.1 相對樹高曲線的定義

在同一林分中，林木各徑階平均高與林分平均高的比值(Rhi)和各徑階平均胸徑與林分平均胸徑的比值(Rdi)之間有較好的相關關系，見公式(1)。

此函數（曲線）稱為相對樹高曲線。研究表明[8]，由于相對樹高曲線可能因樹種等因子不同而產生差異，因此在研究時要分樹種進行模型設計。

1.2.2 模型的基本原理

相對樹高曲線是將胸徑和樹高的具體數值變換成無量綱的相對值，即相對樹高(Rhi)和相對胸徑(Rdi)，由兩者之間的緊密相關性擬合而成。因任何具體林分的相對樹高曲線均通過平均直徑和平均高相對應的1.0這一點上，從而使得差異很大的不同林分樹高曲線收斂為變動范圍很小的相對樹高曲線簇。基于此特性，在進行樣地調查時，只要進行每木檢尺，測定林分平均直徑和平均高，便可由各徑階中值除以林分平均直徑，求得相應的Rdi，將Rdi代入模型Rhi=f(Rdi)便可求得相應的Rhi；再將Rhi乘以林分平均高，即可得各徑階相應平均高，從而實現了利用二元立木材積表估測各徑階和樣地總材積的目的[9]。

1.3 研究資料和數據預處理

1.3.1 研究資料概況

為了建立西洞庭湖區杉木林分相對樹高曲線模型，于2010年8月和2011年8月，對該區森林資源二類調查資料進行了收集整理，并進行實地調研，通過建立臨時標準地(10 m×10 m)，收集了該區不同立地條件下杉木幼、中、成熟林樣地共157塊，其中隨機選取96塊樣地數據作為建模樣本，剩余61塊作為模型適用性檢驗樣本，樣本概況（見表1）。

表1 建模及檢驗樣本分布概況Table 1General distribution of modeling samples and test samples

1.3.2 各樣地數據的預處理

對各樣地進行每木檢尺，每個徑階測3～5株樣木樹高，計算各樣地各徑階樣木平均胸徑和平均樹高，采用繪圖法繪制實測樹高曲線，由樹高曲線查得各徑階中值對應的樹高值，即為徑階平均高。根據各樣地每木檢尺結果，進行斷面積加權求得林分平均胸徑，結合樹高曲線查得對應的林分平均樹高。將每塊樣地的各徑階中值除以林分平均直徑,求出各徑階相對直徑Rdi，各徑階平均高除以林分平均高，求出各徑階相對樹高值Rhi[10-11]（見表2）。

根據表2統計的所有建模樣地相對直徑及相對樹高的分布范圍，可以確定相對直徑的變動范圍主要集中在0.4～1.8，按間距0.2劃分為1個組距（當樣地的實測樹高曲線不滿足相對跨度要求時，采取按曲線趨勢順延的方法補齊）[12]，這樣可以從每個樣地數據中得到8對對應的相對直徑和相對樹高數據，以此標準化數據作為建模的基礎數據，既能夠有效地控制相對樹高曲線的形狀，又能充分利用各樣地提供的信息，提高所建相對樹高曲線模型的質量[13]。

1.3.3 建立相對樹高曲線模型

（1）模型結構的設計。常用的相對樹高曲線數學模型有20多個[14]。經反復擬合優選發現，理查德函數變型的固定參數式是建立該區相對樹高曲線模型的最有效方程，其通式為公式(2)。

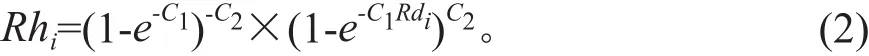
式（2）中：Rhi為相對樹高，Rdi為相對直徑，C1、C2為模型待求參數。

（2）相對樹高曲線模型模擬結果。以相對直徑Rdi為橫座標，相對樹高Rhi為縱坐標，將各樣地的Rdi和Rhi成對值做散點圖（見圖1）。根據圖1所有點的相關趨勢，利用SPSS軟件，模型采用非線性加權迭代回歸估計方法擬合，權函數采用模型本身[15]。擬合結果如表3所示。由表3可得杉木相對樹高曲線模型，見公式(3)。

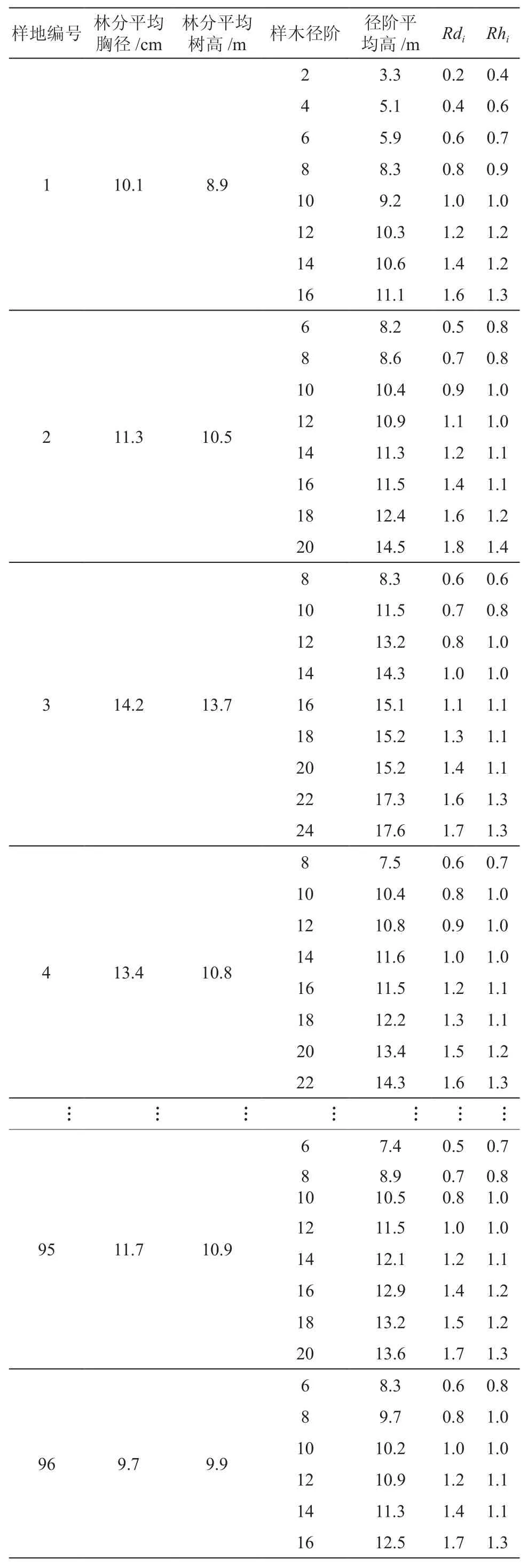
表2 各樣地建模數據統計Table 2Statistics of modeling data from different plots

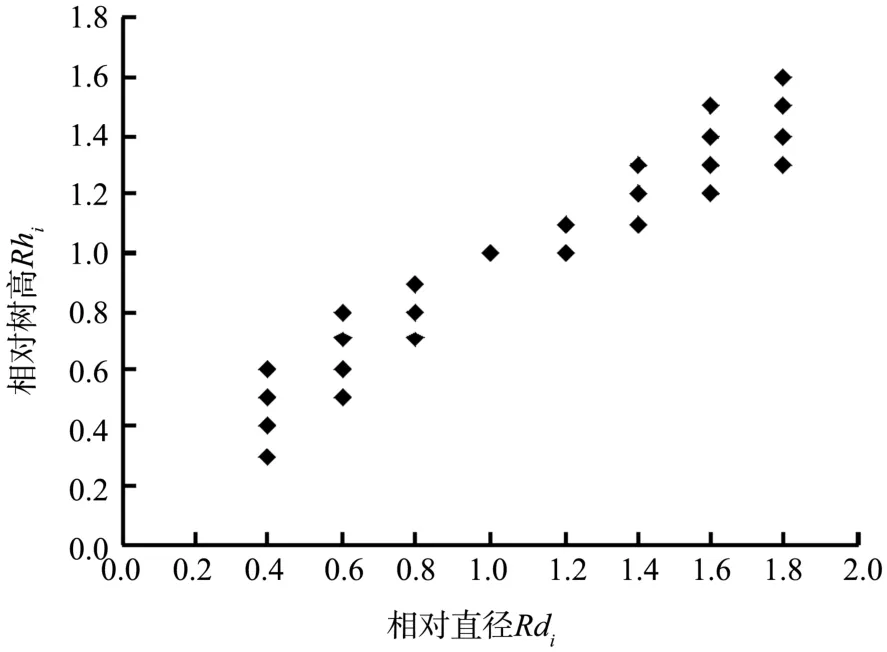
圖1 杉木相對直徑與相對樹高散點圖Fig.1Scattergram between relative diameter and relative height

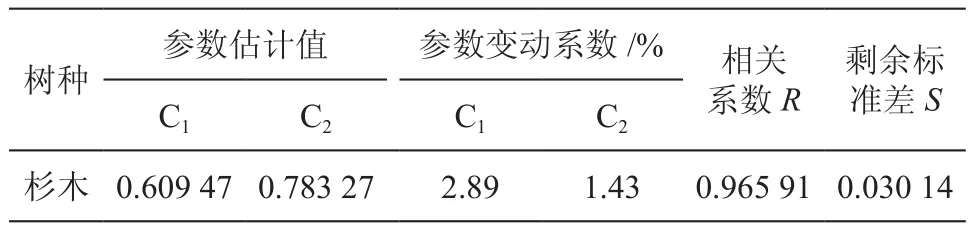
表3 模型模擬結果Table 3Results of model simulation

以擬合結果看模型相關性很好，但對立木材積估測是否有較高的精度，還需測定比較。

2 模型的估測檢驗

以樣地為單位，對剩余61塊杉木樣地（各徑階均勻都有）分別進行材積估計，檢驗模型的適用性。通過以上相對樹高曲線模型進行換算，即可得各徑階相應平均高，結合《湖南省森林資源規劃設計調查技術規定》[16]中二元材積表估測各樣地各徑階立木材積，再由各徑階立木材積相加得各樣地材積[17]，作為估計值。利用樣地每木檢尺記錄的實測胸徑和樹高，結合二元材積表估測得出的各樣地材積值作為真實值，進行成對數據的比較假設檢驗（t檢驗），見公式(4)～(7)。

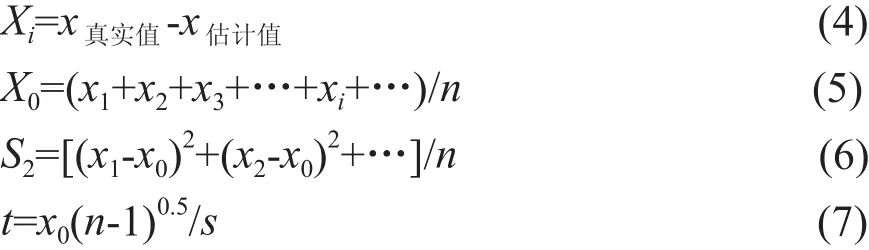
式（4）～（7）中：Xi為每對觀測值之差；X0為所有差的平均值；S2為方差；s為標準差；n為數據對子個數；t為檢驗統計值。計算結果如表4所示。

以上述結果查表得t0.05(60)=2.000，t＜t0.05，表明利用上述相對樹高模型估測的杉木材積估計值與真實值無顯著性差異，精度在允許誤差范圍內，可以在該區使用。

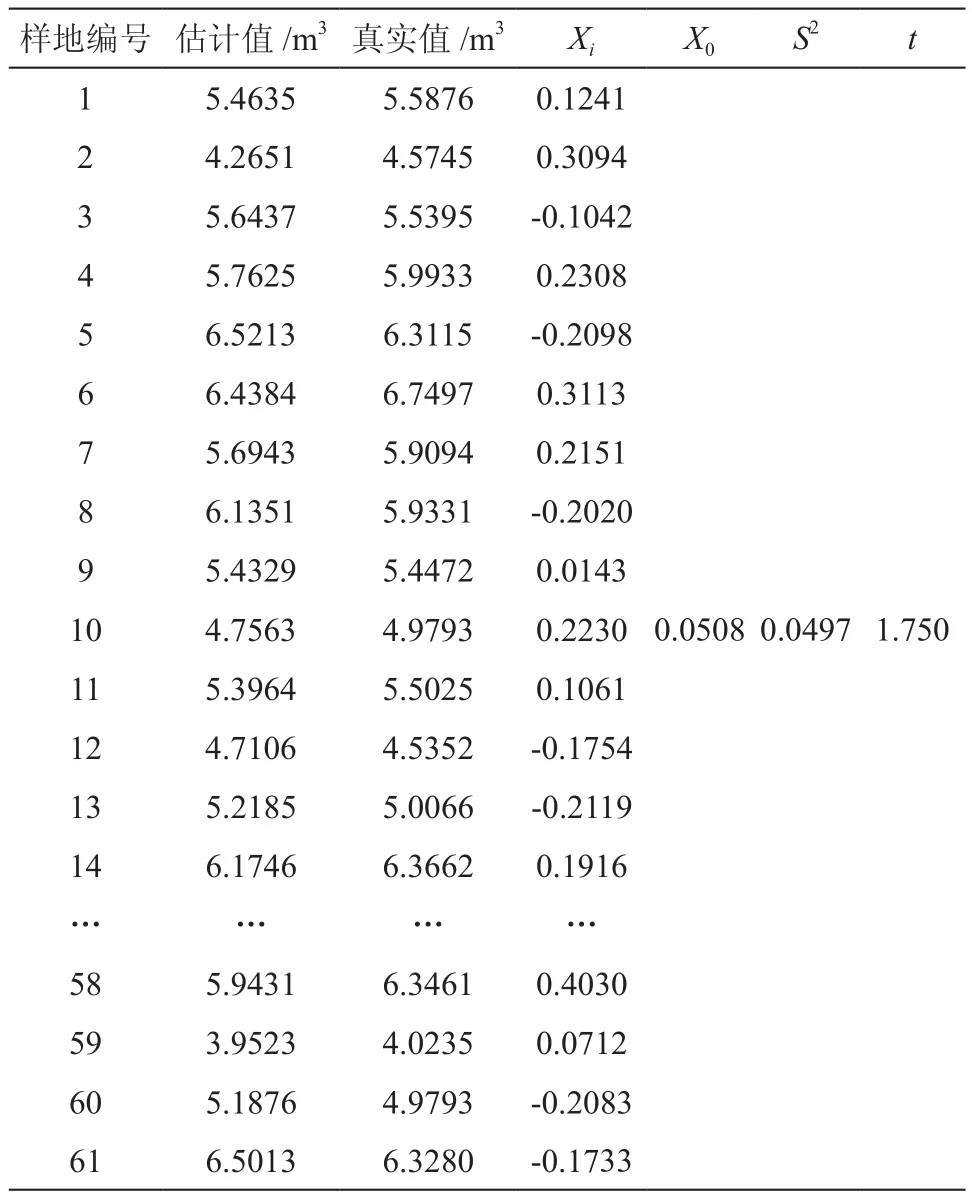
表4 假設檢驗（t檢驗）結果Table 4 Hypothesis testing (t test) results

3 結 論

（1）采用理查德函數變型的固定參數式建立該區杉木林分相對樹高曲線模型，從模型的相關性來看質量較好，模型的預估精度在96%以上，相對誤差在0.5%以內，同時通過利用樣地林分材積估計對模型進行成對數據比較假設檢驗（t檢驗），結果無顯著性差異，表明該模型可達到在該區域應用的精度要求。

（2）利用標準化數據建立西洞庭湖區相對樹高曲線模型，是一種有效可行的新方法，既能有效保證所建模型的質量，又能獲得較高預估精度。模型的建立可廣泛應用于該區杉木林分資源調查、生物量調查等工作中，有重要的實用價值。

（3）由于相對直徑主要集中在0.4～1.8，而相對樹高本身的變動范圍很小，這就為同地區其他樹種合并建立多樹種樹高曲線模型提供了可能。

4 討 論

（1）由于相對樹高曲線模型本身所固有的優良特性，即使采用固定參數模型建模也能滿足精度要求。但由于受地理條件限制，建立具有廣泛適用性的模型，仍是林業工作者需進一步的探索和研究的問題[18]。

（2）在收集建模的樣本時，樣本資料應盡可能覆蓋平均高與平均直徑的整個變化幅度，盡可能收集到最大和最小的平均直徑、平均高的樣地資料，這樣才能建立高質量、高精度的相對樹高曲線模型。但是，由于數據量及調查時間的限制，要獲得研究區較高質量和精度的相對樹高曲線模型，有待于進一步的調查研究。

[1] 程武學,楊存建,周介銘,等.森林蓄積量遙感定量估測研究綜述[J].安徽農業科技,2009,37(16):7746-7750.

[2] 周啟水,潘維旺,阮若江,等.相對樹高曲線模型的建立與應用[J].江西林業科技,1998(4):10-11.

[3] 駱期邦,吳志德.相對樹高曲線模型的研究和應用[J].中南林業調查規劃,1995,14(2):1-3.

[4] 謝哲根,孫孟軍,楊建新,等.林分徑階蓄積量與材種出材量測算的研究[J].中南林業調查規劃,2004,23(2):1-3.

[5] 曾偉生,廖志云.西藏天然林直徑分布模型及其應用研究[J].中南林業調查規劃,2008,27(3):4-7.

[6] 何開倫,魏安世,余松柏.廣東省主要用材林樹種胸徑與冠幅相關性研究及應用[J].廣東林業科技,2006,22(1):33-35.

[7] 陳希英.閩東柳杉人工林林分出材率表的編制研究[J].福建林業科技,2005,32(3):106-107.

[8] 駱期邦,曾偉生,彭長清.可變參數相對樹高曲線模型及其應用研究[J].林業科學,1997,33(3):202-211.

[9] 張志云,歐陽勛志,蔡學林.林分立木材積估計的新方法[J].江西農業大學學報,1999,21(1):100-102.

[10] 宋永俊.相對樹高曲線法在計算林分蓄積上的應用[J].云南林業調查規劃設計,1996,1(1):7-11.

[11] 葉金勝.廣東省主要樹種相對樹高曲線模型的研建[J].廣東林業科技,2006,22(1):26-30.

[12] 岑巨延,李巧玉,曾偉生,等.廣西速豐桉人工林相對樹高曲線模型研究[J].中南林業科技大學學報,2007,27(4):24-27.

[13] 曾偉生,駱期邦,賀東北,等.海南省主要樹種相對樹高曲線模型的建立和應用研究[J].中南林業調查規劃,1999,18(2):1-7.

[14] 駱期邦,寧 輝,賀東北,等.二元立木材積動態模型研究[J].林業科學研究,1992,5(3):263-270.

[15] 曾偉生.再論加權最小二乘法中權函數的選擇仁[J].中南林業調查規劃,1998,17(3):9-11.

[16] 湖南省林業廳.湖南省森林資源規劃設計調查技術規定[M].湖南:湖南林業廳,2004:78-84.

[17] 孟憲宇.測樹學[M].北京:中國林業出版社,2006:132-133.

[18] 謝哲根,劉安興,陳學堂,等.相對樹高曲線研究[J].浙江林學院學報,1998,15(1):69-75.

Study on relative tree height curve model of Chinese fi r stand in west Dongting lake region

SUN Yong-kang, LI Ji-ping, LU Yong
(School of Forestry, Central South University of Forestry and Technology, Changsha 410004, Hunan, China)

In order to obtain a high-precision estimation of stand volume conveniently and quickly in forest resources investigation,based on the data of 96 plots of Chinese fi r stand in west Dongting lake region, the relative tree height curve model for the region was built. The experimental results with hypothesis testing (t-test) show that the accuracy of volume estimate of the model was relatively ideal, and the accuracy was almost as high as that by using tree height curve. The obvious deviation caused by form height variation was avoided when estimating the tree volume in a large regional scope, at the same time, the technical diff i culty and the workload in fi eld was reduced in the practical work.

west Dongting lake region; Chinese fi r; curve model of relative tree height; hypothesis testing

S757

A

1673-923X(2012)09-0047-04

2012-08-15

國家自然科學基金（30972362）；中南林業科技大學研究生科技創新基金資助項目（2010sx04）

孫擁康（1987-），男，河北邯鄲人，碩士研究生，主要從事林業系統工程的研究；E-mail：cssyk2011@163.com。

[本文編校：歐陽欽]