USO-KBR測距系統建模與仿真

辛寧 邱樂德 張立華 丁延衛 覃政

（1 航天東方紅衛星有限公司，北京 100094）

（2 中國空間技術研究院，北京 100094）

1 引言

低-低衛星跟蹤衛星（SST-LL）重力測量衛星是利用衛星測量地球重力場的主要方法之一，對測繪、地震、海洋、水文、地球物理、資源勘探和軍事等均有著非常重要的意義。2002年3月，美德成功發射了基于SST-LL 的“重力恢復和氣候實驗”（GRACE）雙星，用于探測全球重力場。兩顆相同的低軌衛星GRACE-A 和GRACE-B 運行在相同的軌道上，相距約200km 相互跟蹤，以獲得中長周期的高精度全球重力場模型及其隨時間的變化。

K 頻段微波測距（KBR）系統是SST-LL重力測量衛星的關鍵載荷，采用雙頻雙向測量載波相位對比技術，測量兩顆低軌衛星間的距離變化及其變化率，其星間距離測量精度達到10μm。KBR 系統中超穩定振蕩器（USO）作為整個系統的頻率基準，其輸出頻率穩定度直接影響到KBR 系統的測距精度；因此，要研制高精度的KBR 系統，對USO 頻率穩定度及相位測量等仿真研究是不可或缺的環節。GRACE衛星USO的艾倫（Allan）方差達到2×10-13／s，而目前國內所能達到的指標一般為2×10-12／s。文獻［1］研究了基于GRACE衛星的KBR 仿真系統，但其中未涉及USO噪聲及鎖相環相位測量方面的仿真。文獻［2］研究了KBR 系統中載波相位等觀測量的數學模型，但對數學模型描述不清晰，系統仿真結果精度較低。本文對KBR系統內部的USO、鎖相環等關鍵部件進行仿真，并且利用基于衛星軌道動力學基礎上的軌道模型構建仿真場景，建立了高精度觀測數據仿真系統，可為我國重力測量衛星KBR 系統的設計提供仿真分析手段。

2 KBR 系統仿真原理及組成

2．1 KBR 系統仿真原理

KBR 系統采用同步的雙頻雙向對比測距技術，其基本測量原理為：兩顆衛星分別命名為衛星A 和衛星B，每顆衛星發射K／Ka頻段連續微波信號，被另外一顆衛星接收，并測量相位的變化，測量結果傳輸到地面進行綜合處理，從而測量兩顆衛星之間的距離［3］。設A 星和B 星在t時刻發射的微波信號FA（t）和FB（t）的信號振幅為MA、MB，信號頻率為fA、fB，信號初始相位為φ0A、φ0B，則

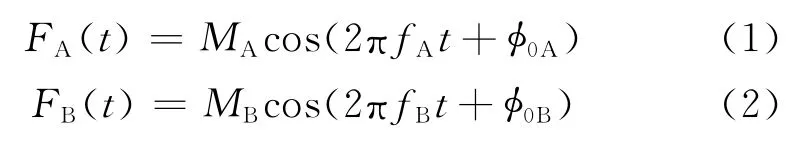
在t時刻，A 星接收到τAB時間（B 星到A 星的傳播時間）前B星發射的微波信號與本地發射信號混頻，相乘得

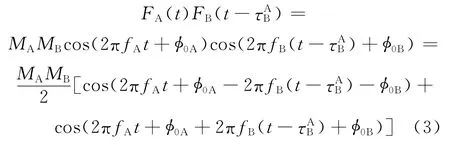
經過低通濾波器濾去高頻分量，可得

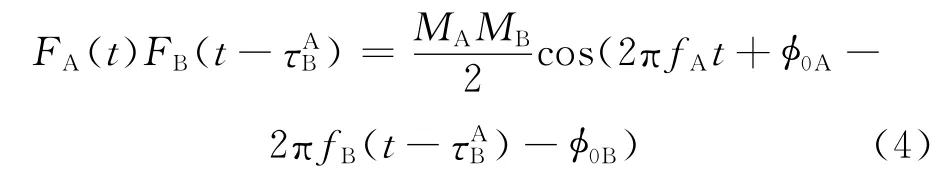
同理，在t時刻，B 星接收到τBA時間前A 星發射的微波信號與本地發射信號混頻，低通濾波相乘可得

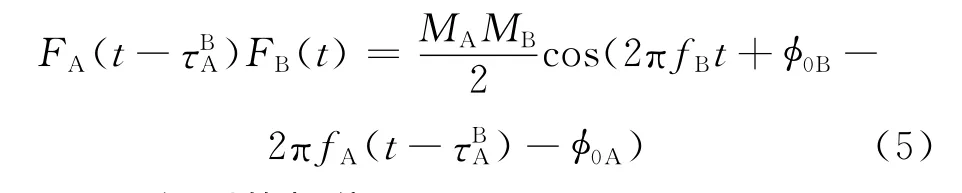
A 星得到的相位

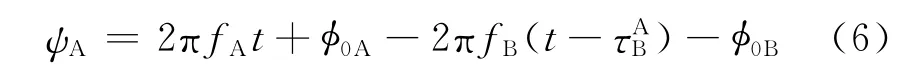
B星得到的相位

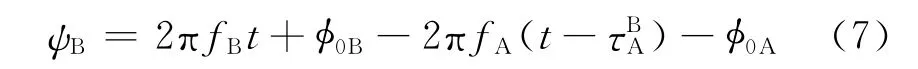
衛星的相位數據下傳到地面進行綜合，得

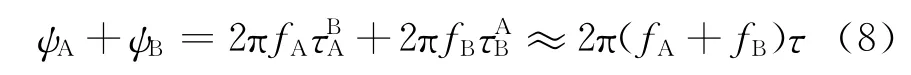
兩顆衛星之間的距離為

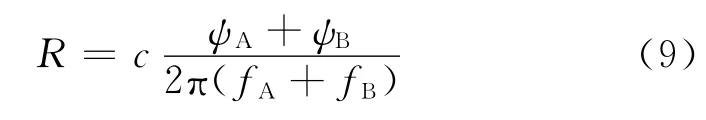
式中：c為光速。

為了去掉電離層的干擾，通常使用雙頻段的距離測量系統。經過電離層修正之后，式（9）可轉換為［3］

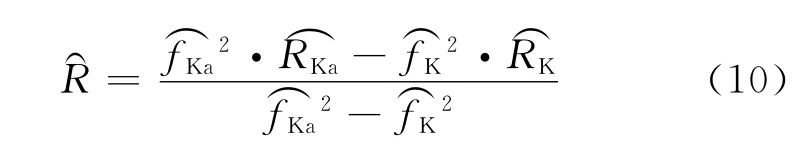
2．2 仿真系統組成

根據KBR 系統進行星間測距的原理，K／Ka頻段雙向相位測量仿真流程如圖1 所示，采樣間隔為0．1s；雙頻雙向星間距離仿真流程如圖2所示。

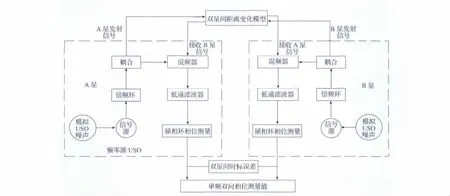
圖1 K／Ka頻段雙向相位測量仿真流程Fig．1 Flow chart of K／Ka dual one-way phase measurements

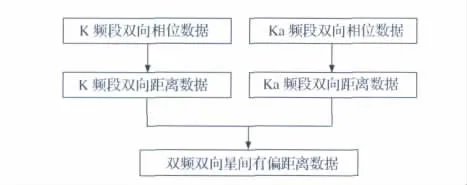
圖2 雙頻雙向星間距離仿真流程Fig．2 Flow chart of dual-band dual one-way inter-satellite range

3 KBR 系統中部件仿真模型

3．1 USO 噪聲模型

USO 中的非確定性噪聲主要包括頻率白噪聲、相位閃爍噪聲和相位白噪聲，相應的噪聲頻域模型為3種冪率譜模型［4］。

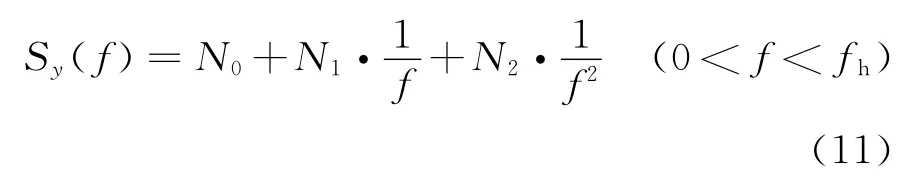
式中：Sy（f）為相對頻率偏差y的譜密度，其中f為USO 的實際頻率值；N0為頻率白噪聲項；N1為頻率閃爍項；N2為頻率白噪聲隨機游走項；fh為振蕩器輸出的上限頻率。

USO 頻率穩定度常用艾倫方差σy2（τ）來表示，其中τ為采樣間隔時間。艾倫方差可以覆蓋振蕩器所有的噪聲過程，也可以直接同功率譜密度互相轉換。振蕩器誤差時域與頻域的換算關系為

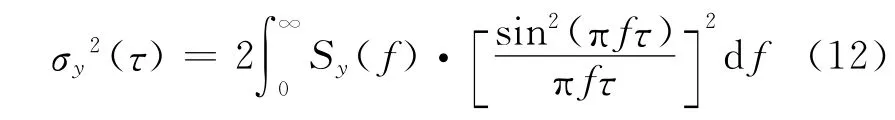
由式（11）、（12）可以推出

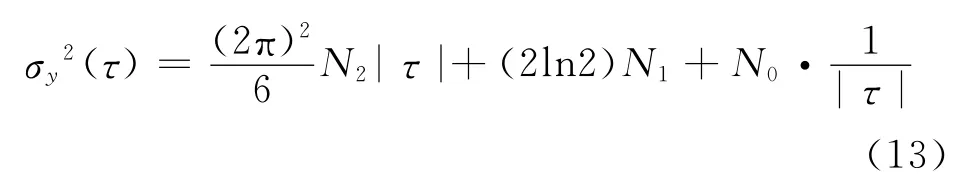
在已知3個以上艾倫方差值時，可采用最小二乘法進行求解，由此可進一步計算任意τ所對應的艾倫方差值和相位噪聲功率譜密度Sy（f）。通過Sy（f）即可計算獲得USO相位隨機誤差的時域模型。

由USO 噪聲引起的系統測距誤差Δρ的功率譜密度為

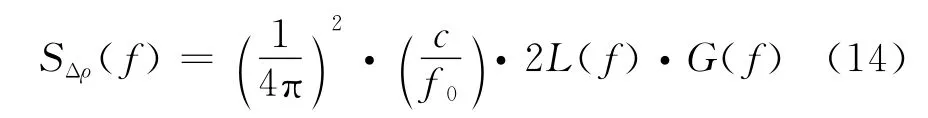
式中：USO的頻率標稱值f0＝4．832MHz；USO實際頻率值f的單邊功率譜密度系統函數

GRACE衛星USO 的艾倫方差如表1所示。

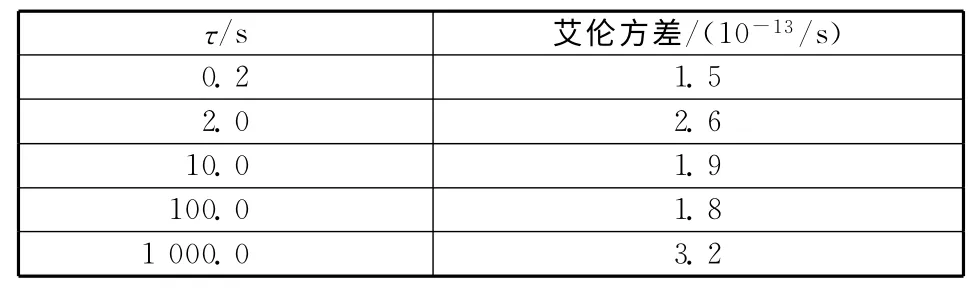
表1 GRACE衛星USO 的艾倫方差Table 1 Allan variances of USO in GRACE

3．2 雙星間距離變化模擬

雙星間距離及其變化率的模擬須建立在衛星精密定軌的基礎上，應用重力場模型及大氣阻力模型等動力學模型，采用龍格庫塔數值積分方法對雙星軌道進行外推，獲取兩顆衛星運行軌道坐標，從而可確定星間距離作為距離參考值。具體的積分公式可參見文獻［5］，仿真所用的雙星軌道參數如表2 所示，重力場模型為GGM02［6］，階數為60×60，大氣阻力模型為DTM 模型。

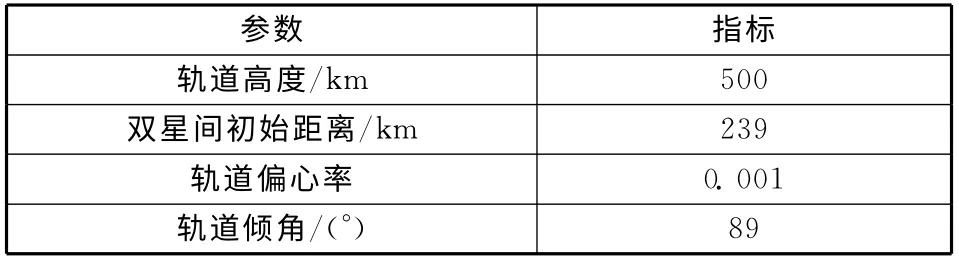
表2 雙星運行軌道參數Table 2 Orbit elements of two satellites

3．3 倍頻環

仿真分析中A 星、B 星的USO 頻率和射頻（K／Ka頻段）頻率如表3所示。

表3 USO 頻率和射頻頻率Table 3 Frequencies of K／Ka band and USO

倍頻環采用標準的Costas鎖相環模型［7］，模型框架如圖3 所示。倍頻后的信號由壓控振蕩器輸出，其中K 頻段的分頻器分頻系數為5 076，Ka頻段的分頻系數為6 768。二階環路濾波器阻尼因子大小為0．707；環路自然頻率為1 000；鑒相器算法為ATAN（Qp／Ⅰp），其中Qp為載波正交信號，Ⅰp為載波同相信號。

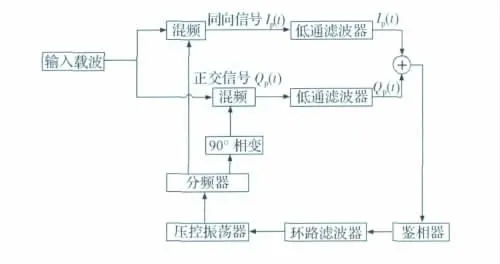
圖3 典型的Costas鎖相環結構Fig．3 Structure of Costas phase lock loop

3．4 鎖相環相位測量

相位測量采用一階鎖頻環與二階鎖相環相結合的測量方式［7］，鎖相環與鎖頻環均采用Costas環結構，其中積分清零時間為0．005s，三階環路帶寬為10Hz，二階鎖相環環路濾波器阻尼因子大小為0．707，環路自然頻率為1 000，鑒相器算法為Qp·Sign（Ⅰp）。

3．5 其他誤差模型

雙星相位觀測值合并時應考慮雙星時間同步誤差修正，利用GPS精密時鐘解可對KBR 相位觀測值時標進行修正；然后再將基于改正后的時標的相位觀測值對均勻分布的標稱采樣時間點進行內插，本文將雙星間的時標誤差定為150ps。系統噪聲誤差利用功率譜密度為的高斯白噪聲進行模擬，多徑傳播誤差為3μm／mrad，雙星天線指向誤差為0．3 mrad［8］，天線相位穩定性誤差、通道時延穩定性誤差及其他不可預計誤差均為1μm。

3．6 仿真系統精度計算

根據文獻［9］提供的KBR 系統的主要誤差公式，利用本文采用的模型參數對KBR 仿真系統的誤差進行分析，結果見表4。

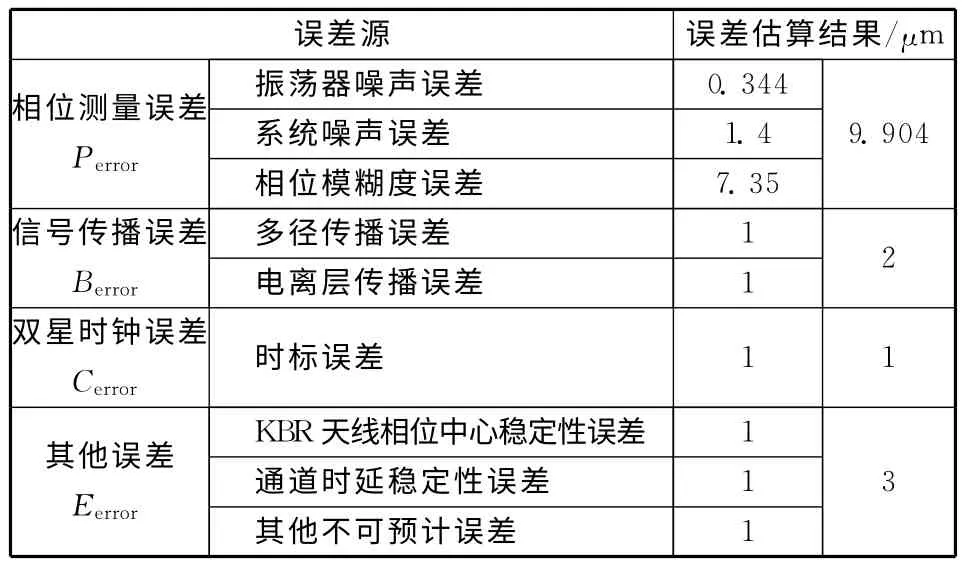
表4 KBR 系統仿真誤差Table 4 Simulation errors of KBR system

KBR 仿真系統的誤差為

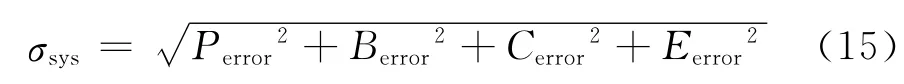
將表4 中估算結果代入式（15），可得σsys≈在重力信號頻段0．000 1～0．1Hz內，測距誤差具有平坦的噪聲譜密度特性，因此，KBR 仿真系統測距精度優于10μm的精度指標要求。

為了保證仿真系統獲得較高的精度，本文主要采取了如下措施：①KBR 仿真系統中使用的數據和模型均參照GRACE 衛星公布的數據；②鎖相環和倍頻環的仿真設計參考了目前GPS接收機的成熟仿真設計模型，達到1／6 000 的測相精度，滿足1×10-3～1×10-4的測相精度指標；③在系統仿真過程中設置時間同步管理機制，保證了各個部件仿真的時間同步。

4 仿真結果分析

USO 噪聲雙邊功率譜密度（PSD）仿真結果見圖4，相位噪聲分析中常使用單邊功率譜作為衡量參數，結果見圖5。

USO噪聲經過雙向對比系統后的雙星距離噪聲功率譜密度見圖6，由USO 漂移導致的星間速率噪聲功率譜密度見圖7。可以看出，雙向對比測量技術能很好地消除USO的中頻和低頻噪聲。

引入軌道參數及動力學模型后仿真的雙星間距離變化如圖8所示。由于軌道周期為5 600s，且軌道偏心率不為0，因此星間距離變化表現為周期5 600s、振幅1km 的余弦波形。

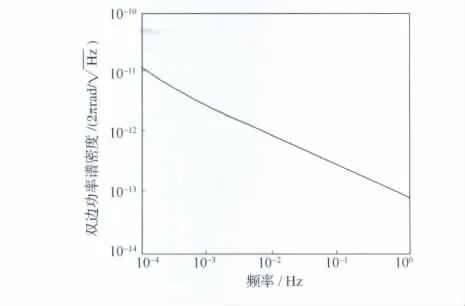
圖4 USO 噪聲雙邊功率譜密度Fig．4 Two-sided frequency spectrum of USO noise

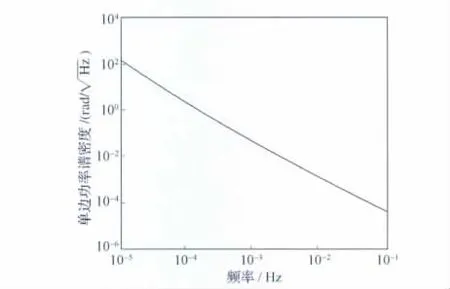
圖5 USO 噪聲單邊功率譜密度Fig．5 Single-sided frequency spectrum of USO noise

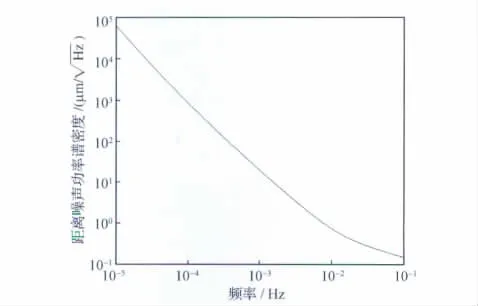
圖6 由USO 噪聲引起的星間距離誤差功率譜密度Fig．6 Power spectral density of inter-satellite range error due to USO noise

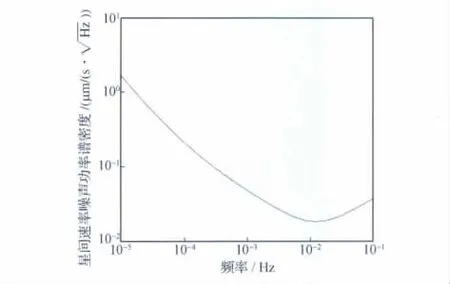
圖7 由USO 噪聲引起的星間速率誤差功率譜密度Fig．7 Power spectral density of inter-satellite range-rate error due to USO noise

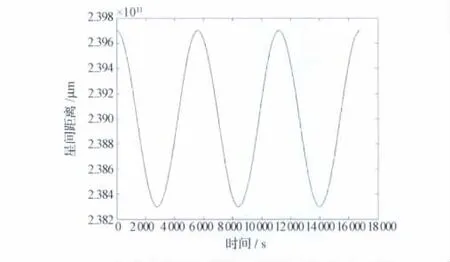
圖8 雙星間距離變化Fig．8 Change of inter-satellite range

單頻單向相位測量仿真結果如圖9所示。由于衛星發射頻率與接收頻率存在頻率差，A 星獲得K／Ka頻段載波相位線性減少，B 星獲得的K／ka頻段載波相位線性增加。測量相位所用的鎖相環會周期性清零，防止載波相位測量值溢出。

雙頻雙向相位測量仿真結果如圖10所示，圖中曲線是通過雙星獲取K／Ka單向載波相位相加得到的，且相位曲線的周期也為5 600s。

單向測距方法與雙向測距方法誤差功率譜密度對比見圖11。由于星間距離變化周期為5 600s，因此雙向測距誤差功率譜［10］的主頻率為10-4Hz。由圖11可以看出：當頻率小于主頻率時，誤差值較高；當頻率大于主頻率時，誤差值迅速降低，接近，相當于系統噪聲。與單向測距方法相比，雙向測距方法能有效地減少低頻和中頻的相位噪聲。將單向及雙向誤差功率譜密度進行傅里葉逆變換，可得到相應誤差的時域分布，對中誤差進行統計，單向測距中誤差為105 632．532 9μm，雙向測距中誤差為9．81μm（與仿真系統計算精度相對應），雙向測距方法與單向測距方法相比，可以極大地降低測距誤差。

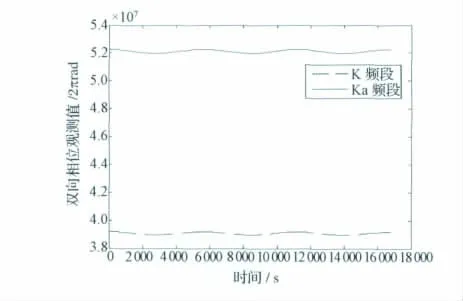
圖9 單頻單向相位測量仿真結果Fig．9 Simulation results of time series of single one-way measurements

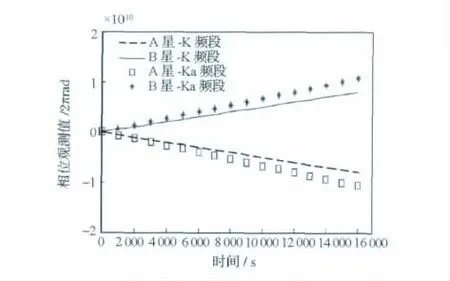
圖10 雙頻雙向相位測量仿真結果Fig．10 Simulation results of dual-band dual one-way phase measurements

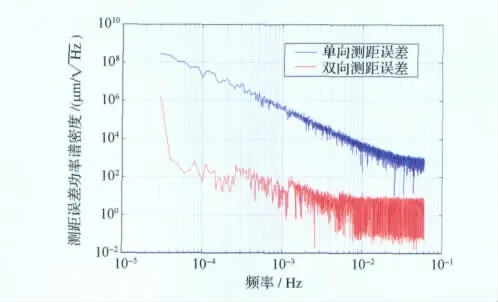
圖11 單向測距與雙向測距誤差功率譜密度對比Fig．11 Comparison of range error power spectral density between single one-way and dual one-way ranging

5 結束語

從KBR 系統的工程設計實際出發，對KBR 系統的關鍵部件進行了建模和仿真研究。從仿真結果可知，本文設計的系統模型及仿真系統具有較高精度。但是，仿真中尚未考慮光時校正誤差模型［11］，在后續的工作中可開展針對這一模型的研究，以得到更精確的仿真結果。本文提出的仿真驗證平臺，可為KBR系統的設計提供參考；通過更改軌道參數和動力學模型，該仿真平臺還可應用到月球及火星重力場探測的研究中。

（References）

［1］Kim J，Tapley B D．Simulation of dual one-way ranging measurements［J］．Journal of Spacecraft and Rockets，2003，40（3）：419-425

［2］康開軒，李輝，鄒正波，等．精密星間微波測距系統觀測數據模擬與預處理技術［J］．大地測量與地球動力學，2011，31（2）：71-75

Kang Kaixuan，Li Hui，Zou Zhengbo，et al．Simulation of measurements and pre-processing technology for high accurate inter-satellite microwave ranging system［J］．Journal of Geodesy and Geodynamics，2011，31（2）：71-75（in Chinese）

［3］佘世剛，王鍇，周易，等．高精度星間微波測距技術［J］．宇航學報，2006，27（3）：402-406

She Shigang，Wang Kai，Zhou Yi，et al．The technology of high accuracy inter-satellite microwave ranging［J］．Journal of Astronautics，2006，27（3）：402-406（in Chinese）

［4］Jeongrae K．Simulation study of a low-low satellite tracking mission［D］．Austin：The University of Texas，2000

［5］Wang Furun．Study on center of mass calibration and K-band ranging system calibration of the GRACE mission［D］．Austin：The University of Texas，2003

［6］Tapley B D．GGM02-an improved Earth gravity field model from GRACE［J］．Journal of Geodesy，2005，79（8）：doi：10．1007／s00190-005-0480-z

［7］Bradford W，James J，Spilker J．Global Positioning System：theory and application［M］．Houston：American Institute of Aeronautics and Astronautics Inc，1996：456-467

［8］Jeongrae K．Flight performance analysis of GRACE Kband ranging instrument with simulation data［J］．Astronautica，2009，65（11／12）：1571-1581

［9］佘世剛．高精度K 頻段星間微波測距技術研究［D］．蘭州：蘭州大學，2008

She Shigang．Study of the technology of high accuracy K band inter-satellite microwave ranging［D］．Lanzhou：Lanzhou University，2008（in Chinese）

［10］Powers E J．Digital time series analysis and applications-class note［M］．Berlin：Springer-verlag，1997

［11］Kim J，Tapley B D．Error analysis of a low-low satellite-to-satellite tracking mission［J］．Journal of Guidance，Control，and Dynamics，2002，25（6）：1100-1106