部分二次特征值及其敏感性配置
謝溪莊
(華僑大學 數學科學學院,福建 泉州 362021)
部分二次特征值及其敏感性配置
謝溪莊
(華僑大學 數學科學學院,福建 泉州 362021)
利用響應矩陣法配置主動振動控制中的配置特征值及其敏感性,使得特征值和敏感性配置的個數不受限制.提出用帶等式約束的二次規劃問題,來求解主動振動控制中單輸入狀態反饋控制系統的部分特征值及敏感性配置問題.數值實驗表明:轉化成二次規劃問題來求解的方法,其特征值配置問題滿足要求,敏感性配置也相對滿足要求.
特征值;敏感性;二次規劃問題;響應矩陣法;主動振動控制
在結構動力學中,許多反特征值問題中都要求系統有特征值的敏感性.例如,在主動振動控制中不僅要求通過引入某種控制器,使得部分系統的特征值可以移動到指定的位置,從而使系統的動態性能得到改善,而且要使特征值的敏感性達到一定的要求.Ram等[1]提出了用響應矩陣法解決主動振動控制中的特征值配置問題.對于主動振動控制中單輸入狀態反饋控制系統的部分特征值及敏感性配置問題[2],Mottershead等[3]提出可以將特征值及其敏感性配置轉化成線性方程,并通過解線性方程組的方式來解決問題.然而,當方程組為超定方程組時,可能出現無解的情況.因此,本文中提出用帶等式約束的二次規劃問題來求解.
1 響應矩陣法
首先考慮二階矩陣微分方程為

式(1)中:M,C,K是n×n實對稱陣,M 是正定的,C,K 是半正定的.通過變量分離z(t)=xeλt,其中λ∈x,x∈xn是一個常向量.由此可得
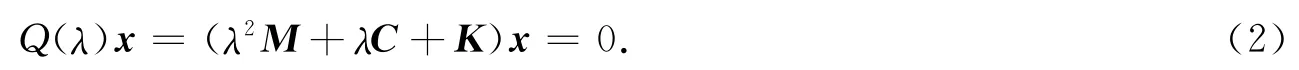
記Q(λ)=λ2M+λC+K,矩陣多項式Q(λ)稱為開環二次束,(λ,x)稱為Q(λ)的特征對.
開環的響應矩陣的形式如下

也可以把它表示成如下形式,即

式(4)中:adj A為矩陣A的伴隨矩陣;det A為矩陣A的行列式.
2 響應矩陣法配置主動振動控制的特征值及其敏感性
考慮單輸入狀態反饋主動振動控制系統為


其中:b,f,g∈Rn.
結合式(5),(6)及變量分離z(t)=xeλt,有

式(7)中:Qc(λ)=[λ2M+λ(C+bfT)+(K+bgT)]為閉環二次束.
由Sherman-Amorrison式

可得閉環的響應矩陣為

部分特征值配置問題就是給定 M,C,K∈Rn×n,向量b∈Rn,集合L={μ1,μ2,…,μp},滿足當μj∈L時,ˉμj∈L且{μ1,μ2,…,μp}∩{λ1,λ2,…,λ2n}=?,其中λi為Q(λ)的特征值.求得f,g∈Rn,使得{μ1,μ2,…,μp}為Qc(λ)的p個特征值.
若{μ1,μ2,…,μp}為Qc(λ)的p個特征值,由文獻[3]可知
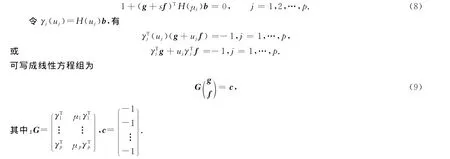
由式(9)可知,當L={μ1,μ2,…,μp}滿足μj∈L,ˉμj∈L時,f和g是實向量,且當p<2n時,線性方程組(9)有無數多個解.另外,由文獻[3]可以得到特征值關于向量g的敏感性為
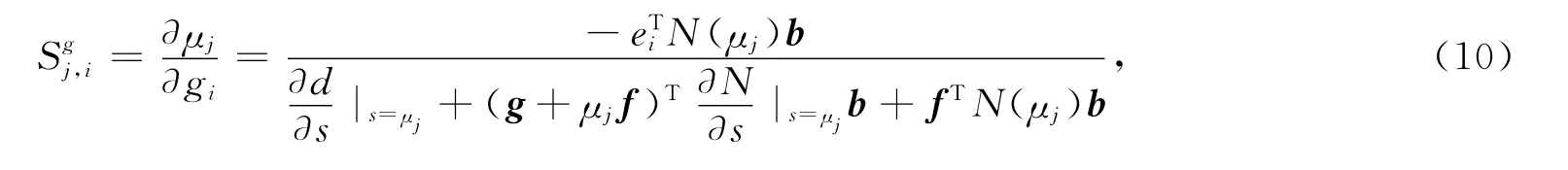
特征值關于向量f敏感性為
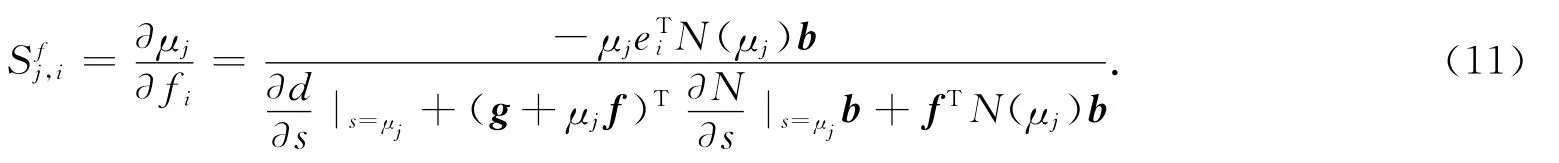

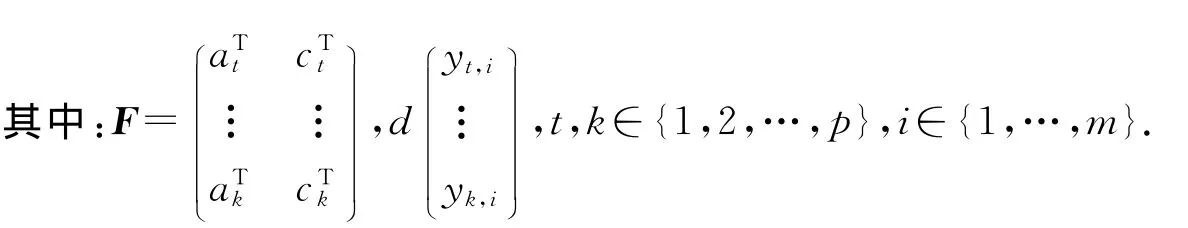
3 帶等式約束的二次規劃問題
對特征值的配置與對其敏感性的配置都可以轉化成求解關于f和g的線性方程組.令u=(gTfT)T,要對兩者同時進行配置時,結合式(9)和式(12)可以求解下面的二次規劃問題[4],即
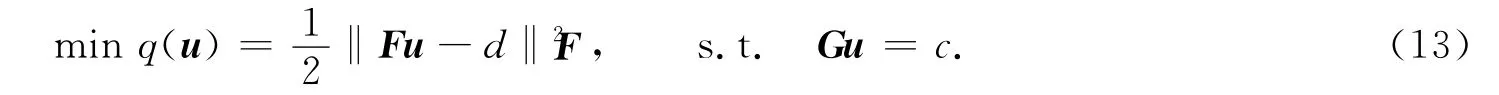
其中:‖·‖F為F-范數.
當F,G是滿秩矩陣時,q(u)是強凸函數,Ω={u∈R2n|Gu=c}是一個閉凸集,二次規劃問題(13)有唯一解,且等價于求解下面的線性方程組,即

其中:FH為f的共軛轉置陣[5].
Mottershead等[3]提出通過下面的線性方程組來求解g和f,即

注1 當F,G不是滿秩矩陣時,可以先將線性方程組(14)的系數矩陣進行QR分解,提取其中滿秩的部分,建立新的二次規劃問題進行求解.
4 數值實驗
設M,C,K,b具有下面的形式,即

其開環的特征值為λ1,2=-0.016 6±0.551 6i,λ3,4=-0.252 8±2.228 9i,λ5,6=-0.252 8±2.228 9i.
例1 將前面4個開環特征值λ1,2,λ3,4替換為u1,2=-0.02±0.8i,u3,4=-0.3±1.9i,給定u3,4=-0.3±1.9i,相對于g的第1個分量的敏感性為.可求解下面的線性方程組(14),得唯一解為

其相應的閉環特征值為u1,2=-0.02±0.8i,u3,4=-0.3±1.9i,u5,6=0.154 3±2.560 1i且u3,4的敏感性.
從上面的實驗可以看出,在例1中,式(13)與式(14)的解是相同的.此時式(13)的目標函數q(u)=1.46×10-6(其值不為0是由于計算機的計算誤差).
例2 在例1的基礎上,再給定u1,2=-0.02±0.8i,相對g的第1個分量的敏感性為.顯然,這種情況下線性方程組(14)是一個超定方程組,無解.只能求解二次規劃問題(13)且可解得

其閉環特征值為u1,2=-0.02±0.8i,u3,4=-0.3±1.9i,u5,6=-0.037 2±2.431 6i;而其相應的敏感性為=-0.05+0.133 5i,=-0.05-0.133 5i,=-0.018 4-0.124 9i,=-0.018 4-0.124 9i.
由此可以看到特征值配置問題滿足要求,敏感性配置雖不是為給定的值,也是比較相對滿足要求的.此時,式(13)的目標函數q(u)=5.06×104.
[1]RAM Y M,MOTTERSHEAD J E.Receptance metheod in active vibration control[J].AIAA Journal,2007,45(3):562-567.
[2]龔德恩.利用矩陣廣義逆的極點配置問題新解法[J].華僑大學學報:自然科學版,2000,21(1):101-106.
[3]MOTTERSHEAD J E,TEHRANI M G,RAM Y M.Assignment of eigenvalue sensitivities from receptance measurements[J].Mechanical Systems and Signal Processing,2009,23(6):1931-1939.
[4]BERTSEKAS D P.凸分析與優化[M].北京:清華大學出版社,2007.
[5]NOCEDAL J,WRIGHT S J.Numerical optimization[J].2nd ed.Berlin:Springer-Verlag,2006.
Assignment of Eigenvalue and Corresponding Sensitivities
XIE Xi-zhuang
(School of Mathematical Sciences,Huaqiao University,Quanzhou 362021,China)
By means of assignment for the eigenvalue and the corresponding sensitivities in active vibration control by receptance method,the number of the assigned eigenvalue and sensitivities isn′t limited.We present an equality-constrained quadratic programming method to solve the problem of eigenvalue and sensitivities assignment in active vibration control using single-input state feedback.It is shown that the eigenvalue and sensitivities can be assigned by the quadratic programming method by numerical tests.
eigenvalue assignment;sensitivity;quadratic programming;receptance method;active vibration control
黃曉楠 英文審校:張金順,黃心中)
O 231.1
A
1000-5013(2012)01-0117-04
2011-05-22
謝溪莊 (1981-),男,助教,主要從事應用數學的研究.E-mail:xzx@hqu.edu.cn.
國務院僑辦科研基金資助項目(09QZR10)

