彈簧質量系統固有頻率忽略自身質量的計算誤差

邱偉華

（柳州職業技術學院，廣西 柳州 545006）

只需要一個獨立坐標，就可完全定義其幾何位置的系統，就是單自由度系統，也就是最簡單的、最基本的離散系統。實際工程中，很多簡單系統可以簡化為單自由度系統，例如簡單彈簧和質量系統。當我們對只包含慣性元件和彈性元件的系統，不考慮阻尼進行討論，這就是最簡單的單自由度無阻尼系統。

筆者介紹了單自由度彈簧質量系統固有頻率的計算方法，并依靠不同的方法，比較了忽略彈簧自身質量以及考慮彈簧自身質量對于固有頻率的影響。

1 無阻尼彈簧質量系統的自由振動[1]

如圖1所示，就是本文要討論的單自由度無阻尼系統。

圖1 彈簧質量系統及簡化坐標

該系統有質量為m的重物（慣性元件）和剛度為k的彈簧（彈性元件）組成。假設不考慮重物的尺寸效應，可以用一個簡單質點來表示這一類重物。為了描述圖示系統位置，采用如圖1所示的單軸坐標系。坐標原點選取在質點靜平衡位置，用x表示質點在任意時刻處于坐標系中的坐標，以向下的方向為正。在此系統運動過程中，x 是時間t的函數，可以稱為質點的位移函數。由于只需要一個空間坐標x，就可以完全確定圖中質點任意時刻的位置，因此可以認為該系統就是單自由度系統。不考慮阻尼的情形下，系統將在初始條件激勵下，圍繞靜平衡點做無阻尼自由振動。

2 振動方程的建立方法[2]

對于簡單系統，振動微分方程的建立主要有2種方法。本文首先進行不考慮彈簧自身質量情形下的微分方程建立方法。

2.1 用牛頓第二定律法建立微分方程

牛頓第二定律又稱運動定律，即物體動量的改變與施加的力量成正比。對于圖示系統，定義質點的靜平衡位置為坐標原點，則質點與坐標原點O的距離為x，可得作用在質點上的彈簧力為[3]

式中，

ξs=mg/k表示彈簧在重物作用下的靜伸長，符號表示力fs的方向始終與（x +ξs）的方向相反，其作用是始終試圖恢復彈簧的原長，一般稱為彈性恢復力。

又由牛頓第二定律有

上兩式運算結果得

式（3）就是圖1所示單自由度無阻尼系統的自由振動微分方程，其是一個二階線性常系數齊次微分方程。為了使得圖1所示系統產生自由振動，需要有一個初始激勵，或者說系統應該有一個非零的初始狀態。初始激勵，也就是初始擾動，通常由t=0 時刻的位移和速度來表示，即為

2.2 用能量法建立系統微分方程

對于本文討論的假設情形無阻尼狀態，那么可以認為是不存在能量耗散，也不會對外提供額外能量，那么系統的機械能是守恒的。機械能守恒的數學表達式為

式中，

Tmax為系統動能最大值；

Umax為系統勢能最大值；

等式含義即是系統的動能最大值等于勢能的最大值。

在此還有另一種表達方式

求導后有

根據圖1的彈簧質量體系，若把坐標原點選在質點的靜平衡位置，選擇質點m的任意時刻坐標為x，可以求得任意時刻系統動能為

假定系統在靜平衡的位置作為勢能零點，對于質點m 處于x位置時刻的系統勢能為

把T 和U 代入（7）可得：

即獲得和式（3）相同的微分方程。

因此，可以得出結論，即使使用方法的不同，不影響同一系統具有相同的運動微分方程。

3 運動微分方程的求解

通過上邊的微分方程建立，可知同一系統的運動微分方程具有唯一形式，下邊將對此微分方程進行求解。

3.1 振動微分方程的求解與振動特性分析

這是一個常系數微分方程，可以直接解出。假設方程（3）具有如下形式的特解

代入式（13）得

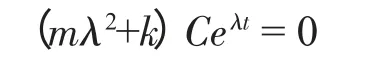
由于系統的振動位移不恒等于零，因此可得

此式即為式（3）的特征方程。解方程易得

此式中

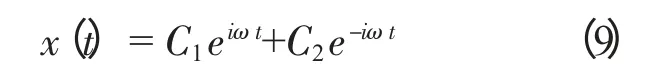
由特征根可以得到式（3）的通解為此式即為質點任意時刻的運動軌跡方程的復數表達方式，式中C1和C2均為待定常數。為了更清楚看出運動的特點，可以用歐拉公式進行轉化，以三角函數來表示運動的軌跡。根據歐拉公式代入式（9）并整理有[4]

由于C1和C2均為待定常數，而且C1和C2必須為一對共軛復數，進一步整理得

式中，C 和D 均為待定常數，進一步三角變化得

式中的A 和φ 均為由初始條件確定的待定常數。

此時可以看出，本文討論的質量體系的運動方式為一個以A為振幅，以ω為固有頻率，以φ為初始相位的無阻尼簡諧振動。其中

即為簡諧振動的固有頻率。

必須強調，以上計算都是以忽略彈簧自身質量作為基礎的。

3.2 考慮彈簧自身質量情況下的固有頻率計算

一般的理論力學考慮中，彈簧自身質量都是不予考慮的。但是在實際工程中，大型彈簧的實際質量很大，在固有頻率的計算中，忽略彈簧自身質量之后的影響非常大，因此有必要給出考慮彈簧自身質量之下的彈簧質量系統固有頻率的計算結果，并和理想狀況下的固有頻率進行對比。

方程的建立，使用能量法。

如圖2所示，可設彈簧長度為l，單位長度的質量為ρ，坐標原點選在系統靜平衡處，當彈簧端點的位移是x的時候，靜平衡時刻距離固定支點端距離為s 處，彈簧位移為sx / l，此處的質量為ρds。

圖2 考慮彈簧質量情況下的計算

此時可知，彈簧的動能為

則系統的總動能為

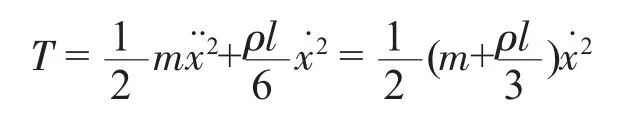
而系統的總勢能為

根據式（7）

以及微分方程求解如文中第3 節計算得考慮了彈簧質量情況下的彈簧質量系統的固有頻率

4 結束語

由上邊計算可以知道，在實際工程中，一旦考慮了彈簧的自身質量，那么簡單彈簧質量系統的固有頻率對比不考慮彈簧自身質量的理想結果，實際中的固有頻率，是低于忽略彈簧自身質量的理想結果的。

[1]諸德超，邢譽峰.工程振動基礎[M].北京：北京航空航天大學出版社，2005.

[2]（美）Singiresu Rao.機械振動[M].李欣業，張明路，譯，北京：清華大學出版社，2009.

[3]尹冠生理論力學[M].西安:西北工業大學出版社，2004.

[4]陳宗煊，劉名生.復變函數[M].北京：科學出版社，2010.