Lambert轉移中途修正的全局概率最優策略

徐 明

(北京航空航天大學 宇航學院，北京100191)

譚 田 李志武

(航天東方紅衛星有限公司 研發中心，北京 100094)

徐世杰

(北京航空航天大學 宇航學院，北京100191)

隨著人類空間活動的發展，航天器對軌道機動能力的需求越來越強.以軌道攔截、遠程交會等飛行任務為例，往往對機動初始、終止位置以及轉移時間有嚴格約束，即Lambert問題.由于Lam－bert轉移不存在解析解［1－2］，眾多學者著重利用優化算法進行求解:參考文獻［3］首先利用遺傳算法得到圓軌道之間的最優轉移;參考文獻［4］通過改進遺傳算法進一步得到Lambert雙脈沖轉移的最優解.但這些研究成果均建立在各種測量誤差已知的假設下;考慮到誤差分布的隨機性，所得到的最優解并不具有普適性.

事實上，在轉移期間施加中途修正，可有效地減少交會的落點偏差:這在地月轉移和拉格朗日點轉移中已有成功應用［5］.中途修正策略的設計包括修正次數、每次軌控時刻以及修正量;本文基于參考軌跡提出線性和非線性3種策略，并應用Monte－Carlo和遺傳算法的聯合仿真，得到實現代價函數(落點誤差最小)在概率意義下的最優解.

與以往直接求解Lambert問題不同，本文將限制性三體問題中求解周期性特解的微分修正算法［6－8］加以改造，得到 J2－Lambert轉移軌道并作為中途修正的參考軌跡.顯然，J2－Lambert轉移軌道基本消除攝動項的影響，則中途修正僅需要補償導航誤差、初始偏差修正的控制偏差等，無需補償攝動力等影響.

1 微分修正算法生成J2-Lambert轉移軌道

根據r0，rf及Δθ可計算二體Lambert轉移軌道［1］.顯然，考慮J2攝動后，該變軌策略將造成較大的偏差.本文基于生成Halo軌道［2］和J2不變軌道［3］的微分修正算法，設計 J2－Lambert轉移軌道.

Lambert變軌策略給出位置交會的轉移軌道，控制量為位置0處的脈沖速度增量Δθ;微分修正算法將改進ΔV及轉移時間Δt=tf－t0，以實現位置f處的交會.Lambert軌道轉移見圖1.

圖1 Lambert軌道轉移

貼近真值的迭代初值，可以保證微分修正算法迭代過程的收斂.由于J2攝動的數量級僅為10－3m/s2，故本文 ΔV的初值取自二體 Lambert變軌策略;為了將探測器導引到目標位置，每次迭代過程都將軌道積分至Rf處，且與Rf具有相同的x(或y，z)坐標分量，而tf即取為該軌道積分時間.顯然，0處軌道速度V0的變化ΔV將導致軌道積分時間tf的變化Δtf.

考查第m次迭代，對轉移末端f處的位置矢量作一階Taylor展開，可得

速度修正量ΔV應使得

整理式(1)和式(2)，可得

實際上，微分修正算法可推廣到更高階引力場模型;但考慮到測量和軌控等誤差對落點偏差的影響大于非球型攝動高階項，即J3－/J4－Lambert轉移軌道并不能明顯改善中途修正的效果;故本文僅利用微分修正算法消除主攝動(J2)項引起的落點偏差.

2 轉移軌道的線性化

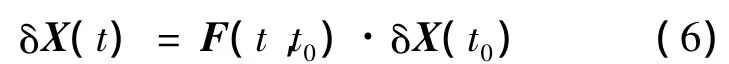
其中，單值矩陣定義為

可通過求解矩陣微分方程得到:

單值矩陣具有如下性質:

3 中途修正策略設計

3.1 基于參考軌跡的線性修正策略I

設Lambert轉移過程中進行k次修正.根據修正次數，整個名義軌道被劃分為k+1段，如圖2所示.

圖2 Lambert轉移中的中途修正

速度增量ΔVm由于修正軌道，以實現探測器在時刻到達目標位置故由式(10)可解得

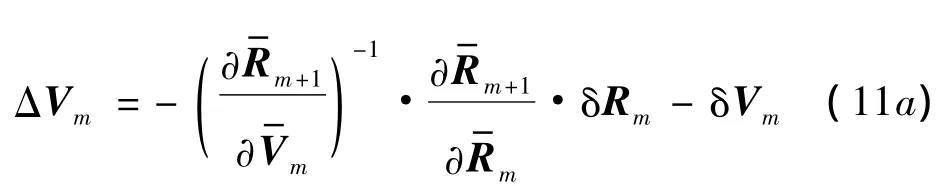
該變種可以看作有k個獨立的修正策略Ⅰ組成，且每個策略僅進行一次修正.

3.2 基于參考軌跡的線性修正策略Ⅱ

為了解決以上問題，本文擬采用隨機最優控制理論設計修正策略Ⅱ.

為了方便表示，將δX記為Y，將 F(tm+1，tm)簡記為F(m+1，m).則探測器運動狀態的一階近似由以下線性差分方程表示:

式中，D(m)=F(m+1，m)·［03×3I3×3］T;白噪聲向量W∈N(0，G)和N∈N(0，Q)分別來源于系統未建模誤差及每次修正引入的誤差和測量誤差.

交會(或攔截)位置精度與燃料消耗的加權關系，由二次型代價函數F0確定，其定義為

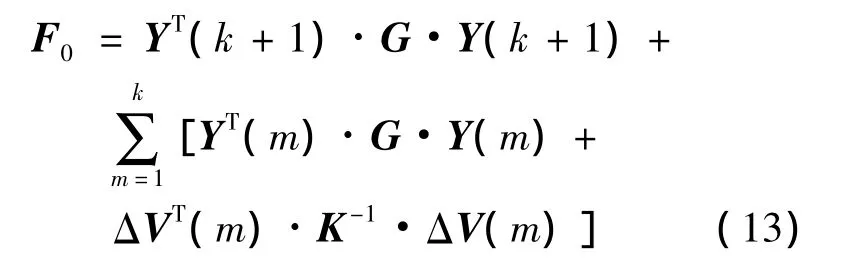
對于該最優問題式(12)～式(13)，可以按照不完全狀態信息情形下離散隨機最優控制的動態規劃法［5，9］求解.求解過程分為以下 3 步:

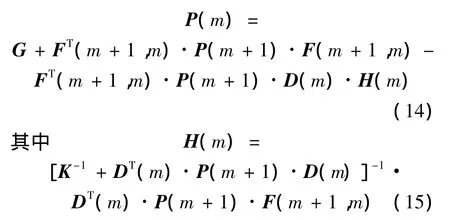
稱為Kalman增益.

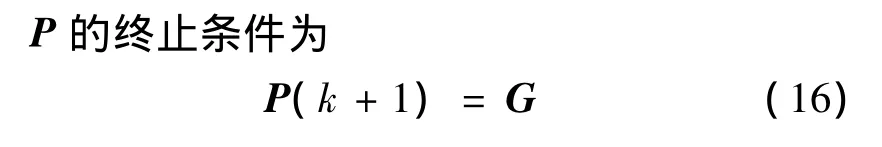
線性最優濾波器:

從而最優速度修正為

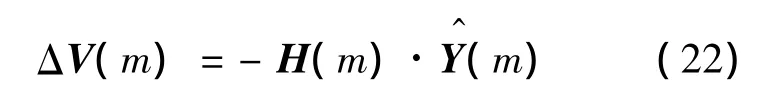
3.3 策略Ⅰ和Ⅱ的關系

不考慮燃料代價，則代價函數F0中加權矩陣取 GR=I3×3，K→∞，即 K－1=0.通過求解 Riccati方程及Kalman增益，可得

式(23)表明，策略Ⅰ本質上是策略Ⅱ的特殊形式.

3.4 基于Lambert迭代的非線性修正策略Ⅲ

微分修正即可設計參考軌跡，還可設計修正策略.整個Lambert轉移過程依次在…，k時刻進行k次修正;對于任意修正點，探測器的狀態記為和，完成該轉移的剩余時間為則根據第1節發展的“J2－Lambert轉移軌道的微分修正生成算法”，可以解算出轉移到期望終端狀態Rf和Vf的修正脈沖ΔVm.

顯然，策略Ⅲ獨立于名義軌道，具有更強的魯棒性;策略Ⅰ(特別是其變種)，僅是策略Ⅲ的一階近似，故策略Ⅲ具有更高精度.策略Ⅰ和Ⅱ僅需進行線性運算，且反饋矩陣經離線設計并裝訂在星上處理器以減少計算量;相反地，策略Ⅲ需要進行非線性的迭代運算，這將耗費相當的計算資源.

4 最優修正時刻選擇

完整的修正策略應包括修正量輸出和修正時刻確定.對于給定修正量輸出策略，希望設計合適的修正點，以實現代價函數在概率意義下的最優.

而修正時刻的確定，需要針對具有不同統計特性的誤差散布來源，對整個隨機過程建立復雜的統計學模型;且中途修正不同于連續控制:對于整個動力系統的演化過程，僅需有限次的不連續控制.因此，很難給出概率意義下最優修正時刻的解析形式，本文將基于Monte－Carlo和遺傳算法的聯合仿真給出數值求解方法.

記εi為最后落點誤差，其中i=90% ～99%，表示該誤差的置信水平.則對于任意的修正時刻τ，存在映射 Θ:τ→εi(τ).顯然，映射 Θ 存在于統計學意義，并且可由Monte－Carlo仿真得到確定.

本文期望找到合適的τ，以使得εi達到最小值.因此，最優修正時刻的選擇轉化為映射Θ的最優化計算;而工程上，置信水平一般取為90%，95%，99%，即該問題本質上是多目標優化問題.幸運地是，遺傳算法的計算結果表明:該多目標最優化模型的Pareto最優解為同一結果，即存在多目標優化最優解.

為了優化算法的實現，需對優化變量修正時刻τ作必要的離散化處理:對整個轉移時間Δt=tf－ t0等間隔離散為 N 段，即└t0，t1，…，tN－1，tf┘;并離線計算出各子區間的單值矩陣F(tm+1，tm)，m=0，1，…，N －1，用于構造修正策略Ⅰ或Ⅱ.

5 仿真算例

根據表1的軌道根數確定Lambert轉移軌道，如圖3所示;整個轉移時間Δt=9 000 s.在J2項攝動的影響下，該轉移軌道將有65.09 km的落點偏差;在21×21階引力攝動下，落點偏差將達到65.134 km;經過“生成 J2－Lambert轉移軌道的微分修正算法”矯正后，該轉移軌道在21×21階引力攝動下偏差僅為35.9243 m.

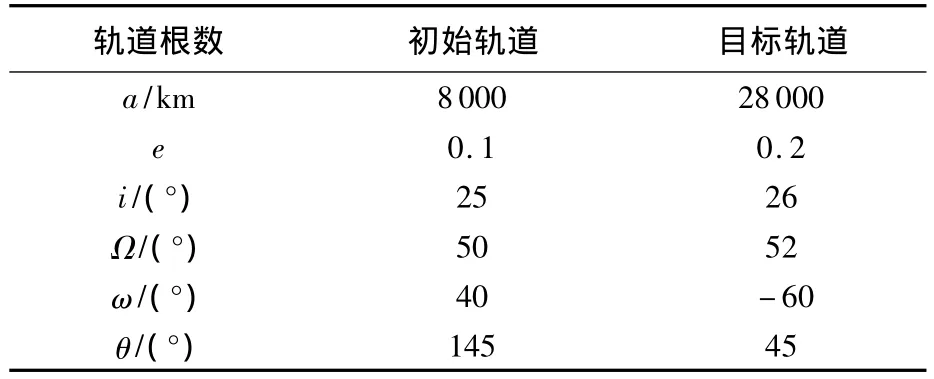
表1 初始軌道和目標瞬時軌道根數

由于存在導航誤差E1和轉移軌道的初始偏差E2以及Lambert脈沖速度偏差E3，將會造成探測器真實飛行軌道偏離名義軌道，故中途修正是必要的;而中途修正將會引入修正速度偏差E4.

以下誤差源認為服從Gauss分布，均值都為零，方差各為:E1和E2的位置偏差200 m，速度偏差0.01m/s(1σ);E3和E4的速度大小偏差0.1%，速度在徑向方向偏差0.573°(3σ).而速度法平面內的偏差滿足［0，2π］上的均勻分布.

本文采用修正策略Ⅰ來制導Lambert轉移，并利用“Monte－Carlo和遺傳算法的聯合仿真”求解最優修正時刻.遺傳算法的參數取為:種群數為40，遺傳代數為25，選擇代溝為0.9，交叉概率為0.7，變異概率為 0.0017;Monte－Carlo 仿真次數為500.優化變量τ的離散間隔N取為300.

優化目標為尋找ε90%，ε95%和ε99%的最小值，而遺傳算法的數值結果顯示:該多目標最優化模型的Pareto最優解為同一結果，即存在多目標優化最優解 τ*=390 s，對應的落點誤差分別為8.82 km(置信度90%)，9.94 km(置信度95%)和10.82 km(置信度99%).最優解的尋優過程見圖4，而最優修正策略的落點誤差分布見圖5.

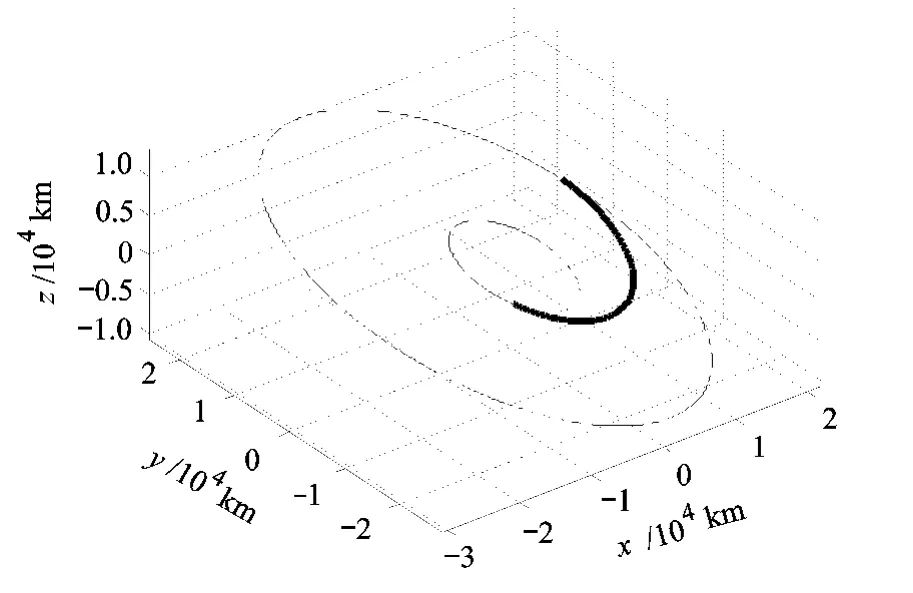
圖3 Lambert轉移軌道

圖4 遺傳算法的尋優過程

圖5 最優修正策略的落點誤差分布

6 結論

本文應用Monte－Carlo法和遺傳算法的聯合仿真求解Lambert轉移中途修正的全局概率最優策略.以往利用優化算法直接求解Lambert問題，需要已知各種測量誤差的大小，即所得到的最優解并不具有普適性.為了有效地減小交會的落點偏差，可在轉移期間施加中途修正.本文針對轉移的最終落點誤差，設計3類中途修正策略以適應不同的精度需要.以第Ⅰ類修正策略為例，應用Monte－Carlo和遺傳算法的聯合仿真，得到在概率意義下的最優修正時刻.

中途修正的參考軌跡設計，基于限制性三體問題中求解周期性特解的微分修正算法構造，以消除攝動項的影響，則中途修正僅需要針對導航誤差、初始偏差修正的控制偏差等進行補償.

本文應通過Monte－Carlo法和遺傳算法的聯合仿真發現“不同置信水平具有相同的概率最優策略”結論;該結論對于設計工程實用的修正策略具有重要意義，而如何從理論上證明上述結論將是下一步的工作重點.

References)

［1］Battin R H.An introduction to the mathematics and methods of astrodynamics［M］.New York:AIAA Inc，1987

［2］韓潮，謝華偉.空間交會中多圈Lambert變軌算法研究［J］.中國空間科學技術，2004(5):9－14 Han Chao，Xie Huawei.Research on algorithm of loopy Lambert transfer in space rendezvous［J］.Chinese Space Science and Technology，2004(5):9 －14(in Chinese)

［3］Spencer D B，Kim Y H.Optimal spacecraft rendezvous using genetic algorithms［J］.Journal of Spacecraft and Rockets，2002，39(6):859－865

［4］陳統，徐世杰.基于遺傳算法的最優 Lambert雙脈沖轉移［J］.北京航空航天大學學報，2007，33(3):273 －274 Chen Tong，Xu Shijie.Optimal Lambert two－impulse transfer using genetic algorithm［J］.Journal of Beijing University of Aeronautics and Astronautics，2007，33(3):273 －274(in Chinese)

［5］Xu Ming，Xu Shijie.Trajectory and correction maneuver during the transfer from Earth to Halo orbit［J］.Chinese Journal of Aeronautics，2008，21(3):200 －206

［6］Xu Ming，Xu Shijie.Nonlinear dynamical analysis for displaced orbits above a planet［J］.Celestial Mechanics and Dynamical Astronomy，2008，102(4):327 －353

［7］Xu Ming，Xu Shijie.Structure－preserving stabilization for Hamiltonian system and its applications in solar sail［J］.Journal of Guidance，Control and Dynamics，2009，32(3):997 －1004

［8］Xu Ming，Xu Shijie.J2invariant relative orbits via differential correction algorithm［J］.Acta Mechanica Sinica，2007，23(5):585－595

［9］Noton M.Spacecraft navigation and guidance［M］.London:Springer，1998