Some New Properties of An E-Convex Function

ZHOU Mi

（Branch College of Technology，SanYa College of HaiNan University，Sanya 572022，China）

Some New Properties of An E-Convex Function

ZHOU Mi

（Branch College of Technology，SanYa College of HaiNan University，Sanya572022，China）

In Ref.1,Youness introduced a class of sets and a class of functions called E-convex sets and E-convex functions by relaxing the de fi nitions of convex sets and convex functions.In Ref.2,Duca and Luspa gave some properties of E-convex functions using two notions of epigraph（epiE（f）and epiE（f））.In this paper,on the basis of the results obtained in Ref.2,some new characterizations of E-con?vex functions are discussed under a relatively weak convexity condition.

E-convex set；E-convex function；nearly convex set；epigraph；slack2-convex set

CLC mumber:O 221.2；O 177.92 Document code:A Article ID：1674-4942（2012）01-0005-04

1 Introduction

The concept of convexity is important for studies in optimization and variational inequalities.To gener?alize the convexity of functions attracted more atten?tions of researchers[1-7].Youness introduced the con?cepts of E-convex sets and E-convex functions in Ref.1.For convenience,we recall some de fi nitions and give other related concepts and lemmas,which are required in the later discussions.

De fi nition 1 Let E∶Rn→Rnbe a function.A subset M?Rnis said to be E-convex if

De fi nition 2 Let M be a nonempty subset of Rnand let E:Rn→Rnbe a function.A function f∶M→R is said to be E-convex on M if M is E-convex and

Lemma 1 [See Ref.1.]If a set M?Rnis E-con?vex with respect to a mapping

E∶Rn→Rnthen E（M）?M，

where E（M）={E（M）|x∈M}

Next,we give another concept of a nearly convex set.

De fi nition 3 A subset M of Rnis said to be near?ly convex,if there is an α∈(0 ,1)such that for all x,y∈M,we have αx+(1 -α)y∈M.

Remark 1 It is easy to check that every con?vex set is also nearly convex,but the converse is not always true.For example,the set

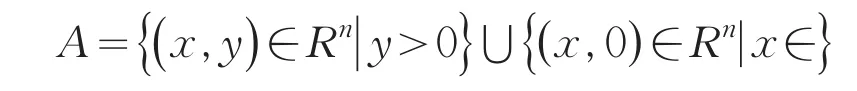
is nearly convex but not convex.

If M is a nonempty subset of Rnand E∶M→M and f∶M→R are two functions.We consider the fol?lowing four sets:

De fi nition 4 If X?Rn,then f∶X→R is said to be upper semicontinuous at-x ∈Xif,for every ε＞0,?δ＞0 such that for all x∈X with x∈B,

In Ref.1,the concept of E-convex sets and E-convex functions were given,its properties were proposed,and the related results were used in the study of E-convex programming.In Ref.2,Duca and Lupsa gave some characterizations of E-convex func?tion using notions of epiE（f）and epiE（f）.In this pa?per,on the basis of the results obtained in Ref.2,we discuss some new characterizations of E-convex func?tions under a relatively weak convexity condition.

2 Main Results

First,let us review the theorem 1[See Ref.2]be?low.

Theorem 1 Let M be a nonempty subset of Rnand let f:M→R and E:Rn→Rnbe two functions.If M is an E-convex set and epiE（f）is a convex set,then f is an E-convex function on M.

We can exclude the convexity hypothesis of the set epiE（f）and in exchange we ask for the set epiE（f）to be near convex and the function f to be upper semi?continuous.

Now see the following theorem as follows.

Theorem 2 Let M be a nonempty subset of Rnand let f∶M→R be an upper semicontinuous function on M,and E:Rn→Rnbe another function.If M is an E-convex set and there exist an α0∈( )0,1 such that

Then,f is an E-convex function on M.

To prove this theorem,firstly we need to intro?duce the following lemma.

Lemma 2 If f is a real-valued function on an E-convex subset M of Rnand if there exists an α0∈（0，1）such that

Thus,we can get that

[1]Youness E A.E-convex sets,E-convex functions and E-convex programming[J].Journal of optimization Theo?ry and Applications,1999,102:439-450.

[2]Duca D I,Lupsa L.On the E-epigraph of an E-convex function[J].Journal of Optimization Theory and Applica?tions,2006,129(2):341-348.

[3]Yong W H.Optimality Conditions for Vector Optimiza?tion with Set-Valued Maps[J].Bull Austral Math Soc,2000,66:317-330.

[4]Chen X S.Some properties of semi-E-convex functions[J].Journal of Mathematical Analysis and Applications,2002,275:251-262.

[5]Noor M A.Fuzzy preinvex functions[J].Fuzzy Sets and Systems,1994,64:95-104.

[6]Abou-Tair I A,Sulaiman W T.Inequalites via convex functions,Internat[J].J Math Math Sci,1999,22:543-546.

[7]Lupsa L.Slack convexity with respect to a given set,Itiner?ant Seminar on Functional Equations,Approximation,and Convexity[M].Babes-Bolyai University Publishing House Cluj-Napoca,Romania,1985:107-114.

E-凸函數的一些新性質

周密

（海南大學三亞學院 理工分院，海南 三亞 572022）

文獻[1]中Youness提出一類E-凸集和一類E-凸函數，削弱了已有的凸集和凸函數.文獻[2]中Duca和Luspa 利用兩種上方圖的概念（epiE（f）和 epiE（f）），給出了E-凸函數的一些性質.本文在較弱的凸性條件上，利用文獻[3]所得結論給出了E-凸函數的一些新性質.

E-凸集；E-凸函數；幾乎凸集；上方圖；松馳2-凸集

2011-10-10

海南省自然科學基金資助項目（110009）

畢和平