大學本科非數學專業《線性代數》課程教學中的思維訓練

蔡美香

(中南林業科技大學 理學院，湖南 長沙 410004)

大學本科非數學專業《線性代數》課程教學中的思維訓練

蔡美香

(中南林業科技大學 理學院，湖南 長沙 410004)

在大學本科非數學專業《線性代數》課程教學中的思維能力的訓練主要是邏輯思維能力與創造性思維能力的訓練。論文對邏輯思維的分析與綜合、分類與比較、抽象與概括，歸納與演繹四種思維過程，創造性思維中的發散性思維和逆向思維分別舉例說明其訓練過程，以期達到提高學生整體思維水平的目的。

《線性代數》；邏輯思維能力訓練；創造性思維能力訓練。

1 引言

美國自然科學基金會最近指出：“當代自然科學的研究正在日益呈現出數學化的趨勢”。數學在當代科技、文化、社會、經濟和國防等諸多領域有著特殊重要的地位。《線性代數》作為高校理工科專業甚至部分文科專業開設的一門數學公共基礎課，著重訓練學生掌握一些有用的運算工具和算法，為學生學習本專業的其他課程提供有力的數學基礎，并為學生處理實際應用問題提供解決多元線性問題的有效工具。同時，《線性代數》課程注重對學生進行邏輯思維能力和創造性思維能力的訓練，這兩種思維能力的培養，將會使學生受益終生。

作為《線性代數》的授課教師，在教學上要注意處理好講授算法和進行思維訓練這兩方面的關系，合理的安排教學時間。在長期的教學實踐中發現，大學本科非數學專業的學生對算法的掌握度普遍較好，而對思維訓練普遍反映較難，部分同學甚至有抵觸情緒。鑒于此，探討在《線性代數》的教學過程中這兩種思維能力的訓練方法是非常有必要的。

2 《線性代數》課程教學中邏輯思維能力的訓練

邏輯思維，是指人們在認識過程中借助于概念、判斷、推理等思維形式能動地反映客觀現實的理性認識過程，又稱理論思維。只有經過邏輯思維，人們才能達到對具體對象本質的把握，進而認識客觀世界。它是人的認識的高級階段，即理性認識階段。邏輯思維能力是指正確、合理思考的能力，即對事物進行觀察、比較、分析、綜合、抽象、概括、判斷、推理的能力，采用科學的邏輯方法，準確而有條理地表達自己思維過程的能力。

邏輯思維能力不僅是學好數學必須具備的能力，也是學好其他學科，處理日常生活問題所必須的能力。邏輯思維能力是在發現問題與解決問題的過程中鍛煉出來的。在《線性代數》的教學過程中，最有效的訓練學生邏輯思維能力的方法是教師提問，由學生獨立思考或相互討論得出答案。具體來說，由于邏輯思維有分析與綜合、分類與比較、抽象與概括，歸納與演繹四種思維過程，下面分別就《線性代數》的教學過程舉例說明。

2.1 分析與綜合

分析是在思維中把對象分解為各個部分或因素，分別加以考察的邏輯方法。綜合是在思維中把對象的各個部分或因素結合成為一個統一體加以考察的邏輯方法。

以行列式按行展開法則的證明為例。考慮的對象為一般的n階行列式應用分析法，將之分解為如下n個特殊的行列式：

分別考慮每一個特殊行列式的值，通過逐行對調與逐列對調，可將第i行的元素aij調到第一行第一列的位置，且除第i行外，其余行的元素的上下左右位置不變，可分別得出如上n個行列式的值分別為提出問題：綜合考慮這n個行列式的和，會有什么結論？這就是行列式按第i行展開公式

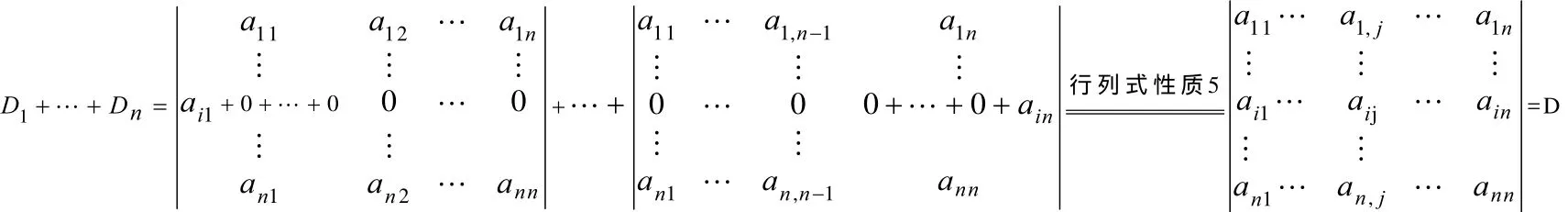
2.2 分類與比較

根據事物的共同性與差異性就可以把事物分類，具有相同屬性的事物歸入一類，具有不同屬性的事物歸入不同的類。比較就是比較兩個或兩類事物的共同點和差異點，通過比較就能更好地認識事物的本質。

以逆矩陣概念的提出為例。眾所周知，數有加、減、乘，除四種基本運算，矩陣也有加、減、乘積運算，唯獨沒有“除”的運算。對于數的除法，有，若b=0，那么a÷b無意義。提出問題：矩陣運算中是否有類似于“倒數”的概念呢？在數字運算中，有一個特殊的數字“1”，當a≠0時，有聯想到矩陣當中有一個特殊矩陣E，它在矩陣中的特殊性類似于數字“1”在數中的特殊性，于是順理成章的提出逆矩陣的概念，若有則記或繼續思考矩陣A存在逆矩陣的充要條件，必要性直接由定義等式兩邊同時做行列式運算可推出充分性需另證（由可得）。當矩陣可逆時，若形式上需要除以一個矩陣，可以用乘上這個矩陣的逆矩陣來做，比如解系數矩陣為方陣的線性方程組當|A|≠ 0時，但是這里不得不比較矩陣乘以逆矩陣與數乘以倒數的差別但前例這是因為數與數相乘是可以交換順序的，而矩陣與矩陣相乘，不一定能交換順序。矩陣形式上的除法本質上是做矩陣乘法，如上例本質上是由等式兩邊同時左乘得來，這里一定要注意是左乘逆矩陣還是右乘逆矩陣。

2.3 抽象與概括

抽象就是運用思維的力量，從對象中抽取它本質的屬性，拋開其他非本質的東西。概括是在思維中從單獨對象的屬性推廣到這一類事物的全體的思維方法。

以用矩陣的初等變換解線性方程組為例，取教材[1]中第三章第一節中引例：

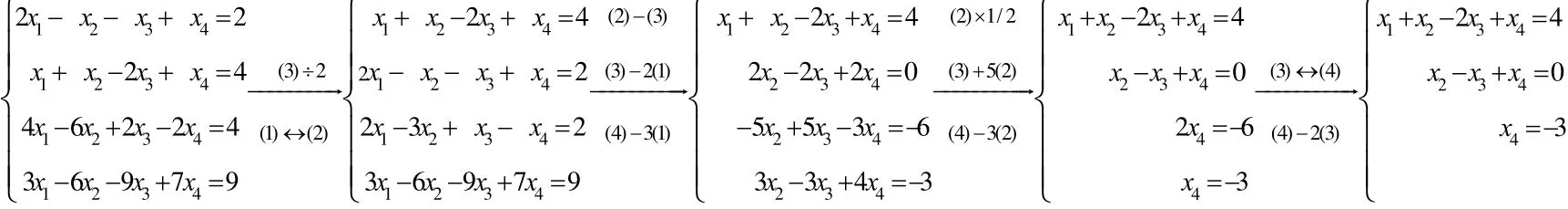
在用消元法解線性方程組的過程中對線性方程組施行了如下三種變換：①交換兩個方程的位置；②某個方程乘上一個不為零的數；③一個方程乘上一個數后加到另一個方程。施行這三種變換后得到的新的線性方程組與原方程組是同解的。我們對如上過程進行抽象分析，就會發現，消元的本質就是通過如上三種變換將某個方程的某個未知變元的系數變為0。若固定未知變元的順序，第1-4列分別代表第五列代表常數項b，實際上以上過程只是對方程組的系數和常數進行運算，未知數并沒有參與運算。于是，可將方程組的系數和常數構成一個增廣矩陣，對增廣矩陣施行如下相應的初等行變換：

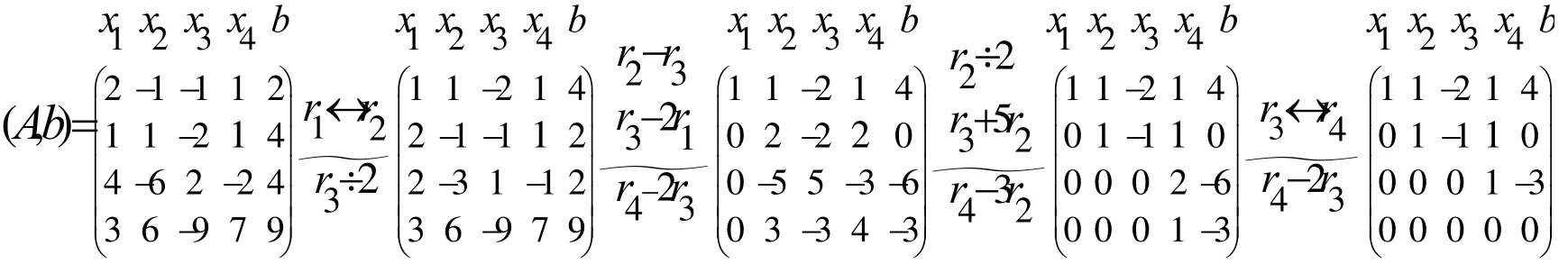
繼續施行行初等變換直到將矩陣化成行最簡形，得出方程組的通解。對如上過程進行概括總結，可以將矩陣的初等行變換應用到解一般的具有n個未知變元，m個方程的線性方程組中。同時，提出問題：“是否可以應用矩陣的初等列變換來解題呢？”只要學生對這種方法的本質把握好了，相信不難得出“前n-1列可以交換，但要注意各列所代表的未知變元要跟著走，最后一列代表常數列，不可以和前面的列進行交換”的正確答案。這里還可繼續對學生進行創造性思維的訓練：提出問題：矩陣的初等列變換對不同形式的通解起了一個什么樣的作用？學生會繼續思考：行階梯形矩陣中階梯口所在的列所代表的未知變元為非自由未知量，應用矩陣的初等行變換解線性方程組，有盡量選擇前面的未知變元做非自由未知量的趨勢，而矩陣的初等列變換可能會改變非自由未知量的選擇，因此可能會得到不同形式的通解。

2.4 歸納與演繹

歸納是從個別性的前提推出一般性的結論，前提與結論之間的聯系是或然性的。以非齊次線性方程組Ax=b解的結構為例。提出問題：能否由齊次線性方程組Ax=0的通解歸納得出Ax=b的通解？若Ax=0的通解為設Ax=b的任意的一個解為的一個特解，那么必為的解，可以得到于是得出非齊次線性方程組Ax=b解的結構：非齊通=齊通+非齊特。

演繹是從一般性的前提推出個別性的結論，前提與結論之間的聯系是必然性的。以矩陣的對角化與對稱矩陣的對角化為例。我們知道，n階矩陣A能夠對角化的充要條件是存在n個線性無關的特征向量構成可逆矩陣使得這是對任意矩陣的一個一般性的結論。提出問題：對稱矩陣對角化時有什么更特殊的結論嗎？由于對稱矩陣的特征值全為實數，且不同的特征值所對應的特征向量是正交的，可以得出一個更特別的結論：對稱矩陣一定可以對角化，且存在矩陣P，不但是可逆的，而且是正交的，使得

3 《線性代數》課程教學中創造性思維能力的訓練

創造性思維是一種具有開創意義的思維活動，即開拓人類認識新領域，開創人類認識新成果的思維活動。狹義上，它往往表現為發明新技術、形成新觀念，提出新方案和決策，創建新理論。從廣義上講，創造性思維不僅表現為作出了完整的新發現和新發明的思維過程，而且還表現為在思考的方法和技巧上，在某些局部的結論和見解上具有新奇獨到之處的思維活動。

在《線性代數》課程的教學過程中主要是嘗試訓練學生廣義上的創造性思維。學生形成創造性思維的主要條件是強烈的好奇心、堅強的信念和永不滿足的求知欲，以及有關的廣博知識，主要表現在想像、尤其是創造性想像的參與。對于非數學專業的學生，除了要關注一般人才的培養，還需重視各類優秀人才的培養問題。對學生創造性思維的訓練，為優秀人才的迅速成長創造了良好的條件，營造了良好的環境。在《線性代數》課程的教學實踐中，對學生創造性思維的訓練，主要表現在對學生發散性思維和逆向思維的引導上。

3.1 發散性思維

發散性思維由美國著名心理學家Guiford于1967年提出，創造性思維的本質是發散思維，又稱求異思維、擴散思維等，是指沿著各種不同的方向去思考，重組眼前的信息和記憶系統的信息，從而產生出大量獨特的新思想。它克服了常規思維中單向思維的缺陷，是一種不依常規、尋求變異，從多方面探索答案的思維形式，是創造性思維的重要組成部分。

“一題多解”是發散性思維的一種典型表現，體現在課程內容上，即“一個內容，多種解釋”。以最簡單的解線性方程組為例，繼續將前述引例進行初等行變換，直至化成行最簡形，可得與原方程組同解的線性方程組為

3.2 逆向思維

逆向思維，是指在思維活動時，從相反方向去觀察和思考，避免單一正向思維和單向度的認識過程的機械性，這樣往往獨具一格，常常導致創造性的發現，取得突破性的成果。逆向思維也是創造性思維的組成部分。

則逆向命題不成立。這里可以繼續引導學生分別就這兩種情形舉出示例。

[1]同濟大學數學系.線性代數[M].北京:高等教育出版社,2007.

[2]課題組.數學學科專業發展戰略研究報告[J].中國大學教學,2005,(3):4-9.

[3]鄔學軍,唐明.線性代數是藍色的——大學非數學專業《線性代數》的課程設計[J].大學數學,2008,(6):12-16.

[4]皋古之.線性代數教學中學生創新思維的培養[J].新思路,2011,(10):38-39.

[5]李毅夫.線性代數教學中培養學生的發散思維[J].高師理科學刊,2007,(6):103-105.

[6]喻光偉.線性代數中的一些邏輯形式分析[J].教育與人才,2009,(25):107-108.

G642

A

1673-2219（2012）08-0013-04

2012－04－05

中南林業科技大學人才引進基金，編號104-0163。

蔡美香（1981－），女，湖南邵陽人，博士，主要從事動力系統的分支和混沌理論研究。

（責任編校：京華，俊華）