有限域上線性q-相伴多項式及其應用

陳引蘭

(湖北師范學院 數學與統計學院,湖北 黃石 435002)

1 由q-相伴多項式構造高次不可約多項式或本原多項式

有限域上的不可約多項式作為有限域上多項式環的素元，在構造有限域和計算有限域中的元素時都是必不可少的，而且在密碼、編碼理論及隨機數的產生等方面也有著廣泛的應用[1～3]。

關于有限域Fq上不可約多項式的存在性問題，設n是給定的正整數，d|n，記Nq(n) 為Fq上所有n次首1不可約多項式的個數，μ(d) 表示莫比烏斯函數。我們有：

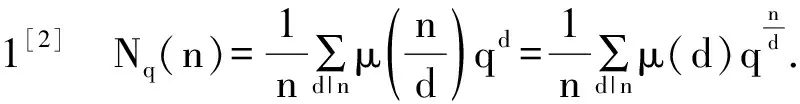
由此可知，有限域Fq上n次不可約多項式存在，而且隨n增大而增加，但要構造出任意次數的所有不可約多項式仍然是困難的。本節利用線性q-相伴多項式由低次不可約或本原多項式構造高次不可約多項式或本原多項式。為此，先介紹線性q- 相伴多項式。

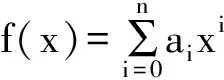
定理1[2]設f(x)是Fq[x] 上不可約多項式，F(x)為f(x) 的線性q-相伴多項式，記g(x)=F(x)/x，則g(x)的任一不可約因式的次數均為ord(f(x)) .

注 在Fq[x] 中，使得f(x)|(xn-1) 的最小的正整數n稱為f(x)的階，記為ord(f(x)) .

本原多項式一定是不可約多項式，但不可約多項式不一定是本原多項式。Fq上n次本原多項式是Fq上所有n次不可約多項式中階最高(qn-1) 的多項式。下面的結論推廣了文[3]中的結論(定理3)。

定理2 設f(x) 是Fq[x] 上不可約多項式，且f(0)≠0，則g(x)=F(x)/x在Fq[x] 上不可約的充分必要條件是f(x) 是Fq[x] 上的本原多項式或本原多項式的非零常數倍。

證明 充分性:設f(x) 是Fq[x]上的本原多項式或本原多項式的非零常數倍，且deg(f(x))=n，則f(x)為Fq[x]上的不可約多項式，且ord(f(x))=qn-1.由定理1知：g(x)的任一不可約因式的次數均為ord(f(x))=qn-1，而deg(g(x))=qn-1，所以g(x) 為Fq[x] 上的不可約多項式。

必要性:設g(x)=F(x)/x在Fq[x] 上不可約，又f(x)是Fq[x]上不可約多項式，且f(0)≠0，由定理1知： deg(g(x))=ord(f(x)),而deg(g(x))=qn-1，所以ord(f(x))=qn-1，即：f(x) 為Fq[x] 上n次qn-1 階且f(0)≠0的不可約多項式。

若f(x)是首1的，則f(x)是Fq[x]上的本原多項式；

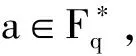
定理得證。

對于定理2，何時g(x) 仍為Fq[x]上的本原多項式呢？當f(x)是Fq[x]上的本原多項式或本原多項式的非零常數倍時，將g(x)看作定理中的f(x) ，不難得到:

定理3g*(x)=G(x)/x在Fq[x] 上不可約的充分必要條件是g(x)=F(x)/x為Fq[x] 上的本原多項式。其中G(x)是g(x)的線性q-相伴多項式。

特別地，若f(x) 是F2[x] 上的n次本原多項式，且f(0)≠0，則g(x)=F(x)/x為F2[x]上的 2n-1次不可約多項式，當 22n-1-1為素數時，2n-1 一定為素數(見文[4])，此時有ord(g(x))|(22n-1-1)，而22n-1-1 為素數，且ord(g(x))>1，所以ord(g(x))=22n-1-1，即g(x)為Fq[x] 上的本原多項式，故g*(x)=G(x)/x在Fq[x]上不可約。于是有

推論1 當 22n-1-1為素數時，若f(x) 是F2[x] 上的本原n次多項式，則g(x) 為F2[x] 上2n-1 次本原多項式。

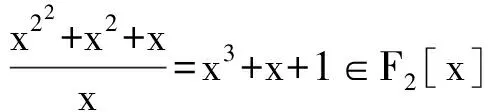
2 由 q-相伴多項式求兩高次多項式的最大公因式

先證明多項式與其q-相伴多項式的整除關系等價。文[2]中下面的結論是借助形式除法的定義給出證明的。這里我們直接證明該結論。

定理4 設L1(x),L2(x) 分別是Fq[x]上多項式l1(x),l2(x)的線性q-相伴多項式，則下列條件等價：

1)L1(x)|L2(x);

2)l1(x)|l2(x).

若L1(x)|L2(x),設l2(x)=l1(x)·h(x)+r(x) ，其中0≤deg(r(x))

反之，若l1(x)|l2(x) ，設l2(x)=g(x)·l1(x) ,則L2(x)=G(L1(x))，其中G(x)是多項式g(x)的線性q-相伴多項式，于是L1(x)|L2(x).

由定理4，我們容易得到下面求最大公因式的定理。

定理5 設L1(x),L2(x) 分別是Fq[x]上多項式l1(x),l2(x)的線性q-相伴多項式，且 (l1(x)，l2(x))=h(x),則(L1(x),L2(x))=H(x)，其中H(x)是多項式h(x)的線性q-相伴多項式。

由定理5知，要求某些高次多項式的最大公因式，而他們是某些多項式的線性q-相伴多項式，從而轉化為求次數低的原多項式的最大公因式，比直接求大大減少了計算量。

例2 求多項式L1(x)=x64+x16+x8+x4+x2+x∈F2[x],L2(x)=x32+x8+x2+x∈F2[x] 的最大公因式。

解 在F2[x]上，與L1(x),L2(x)線性q-相伴多項式分別是l1(x)=x6+x4+x3+x2+x+1,l2(x)=x5+x3+x+1,由輾轉相除法，得(l1(x),l2(x))=x+1. 于是,(L1(x),L2(x))=x2+x.

參考文獻:

[1]萬哲先.代數和編碼[M].北京:高等教育出版社，2007.

[2]Lidl R,Niedrreiter H.Finite Fields[M]． Cambridge:Cambridge Univ Press, 1997.

[3]郭寶安，蔡長年.有限域上的不可約多項式[J].北京郵電大學學報,1994,1(17):23～26.

[4]閔嗣鶴，嚴士健.初等數論(第三版)[M]．北京:高等教育出版社，2005.