基于GM(1,1)數據融合算法的滑坡預測研究
王騰軍,賴百煉,葉俊華,楊志強
(1.長安大學地質工程與測繪學院,陜西西安710054;2.中國煤炭地質總局航測遙感局,陜西西安710054)
基于GM(1,1)數據融合算法的滑坡預測研究
王騰軍1,賴百煉2,葉俊華1,楊志強1
(1.長安大學地質工程與測繪學院,陜西西安710054;2.中國煤炭地質總局航測遙感局,陜西西安710054)
滑坡會對人類生命和財產造成巨大損失,預測預報是預知滑坡災害發生并減少其影響的重要手段。GM(1,1)算法在滑坡預測中得到普遍應用,該算法具有較少數據量建模的優點。對于滑坡不需要了解各種影響因子的具體狀態,但存在建模數據量選取不確定性和長時距預測精度降低的問題,以GM(1,1)模型為基礎,引用數據融合技術,對滑坡變形量進行預測,并用實測數據進行驗算,結果表明該方法能提高滑坡的預測精度。
GM(1,1);數據融合;滑坡變形;變形預測
一、引 言
滑坡作為一種自然地質災害,常常會造成巨大的生命財產損失,已成為僅次于地震的第二大自然災害。為了預防災害的發生,很有必要事先對滑坡發生的時間做出預測預報。經過國內外許多專家學者的幾十年的潛心研究、探索,提出了多種滑坡預測預報的理論模型和方法[1],可概括為以下4種:確定性預測預報模型;統計預報模型;非線性預報模型;宏觀預報模型。在統計預測預報模型中,代表性的有灰色GM(1,1)模型、回歸分析法、指數平滑法等多種方法。
GM(1,1)模型數據需求量低,一般幾個數據就可以建立模型,直接從所面對的數據中提取信息,其適用于中短期和臨滑預測預報[1]。對于GM(1,1)模型進行中長期預測預報精度較差的問題,可以通過實測值迭代和數據融合技術加以改化,數據融合(data fusion)是利用計算機技術將來自多個傳感器或多源的觀測信息進行分析、綜合處理,從而得出決策和估計任務所需的信息的處理過程,它往往能獲取比單一數據更加可靠的結果[2-3]。
由于GM(1,1)模型長期預測的有效性明顯受到系統時間序列長短及數據變化的影響,因此如果系統建模運用數據列太短,則難以建立長期的預測模型;數據列過長,系統干擾的成分太多,不穩定因素大,易使模型精度降低[4]。針對選取多少數據建立模型,文中所采取的方法是迭代入實測值后構成等維灰色遞補動態預測,在遞補數據基礎之上選擇不同量的數據序列建立多個預測模型,而后對不同模型的預測結果進行數據融合,以獲取更加準確的預測值。
二、GM(1,1)基本模型[5-6]
若假設 x(0)(k)為測量的滑坡位移值,由x(0)(k)構成的非負序列X(0)為

式中,x(0)(k)≥0,k=1,2,…,n。
設X(1)為X(0)的一階累加生成序列
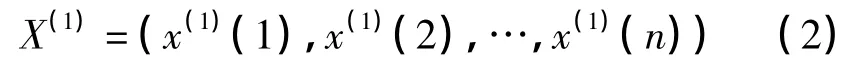
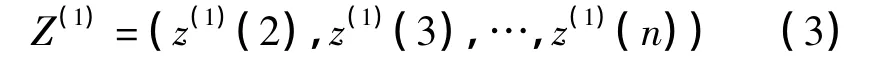
式中,z(1)(k)=0.5(x(1)(k)+x(1)(k-1)),(k=2,3,…,n)。
若 ^Α=[a b]Τ為參數列,且
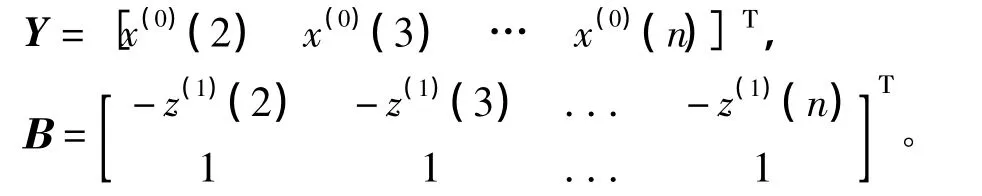
則GM(1,1)模型
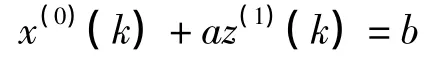
的最小二乘估計參數列滿足

那么GM(1,1)模型的白化方程為
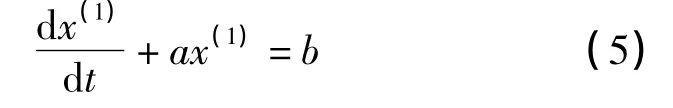
由白化方程得到時間響應函數
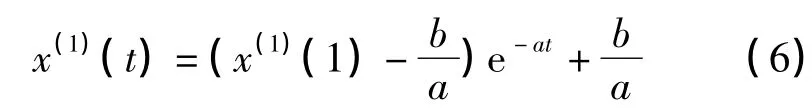
可以得到GM(1,1)模型x(0)(k)+az(1)(k)=b的時間響應序列為

那么還原值為

三、GM(1,1)數據融合預測算法

式中,i,j∈{1,2,…,m}。
構造兩個數據間的支持度函數rij,其必須滿足以下兩個條件。
1)rij與相對距離成反比關系,即兩個值相差越大,彼此之間支持程度越小。
2)rij∈[0,1],使數據的處理能夠利用模糊集合理論中隸屬函數的優點,避免數據之間相互支持程度的絕對化。
rij的選取可以由很多種,以下為最簡單的兩種形式[7]。
階躍型
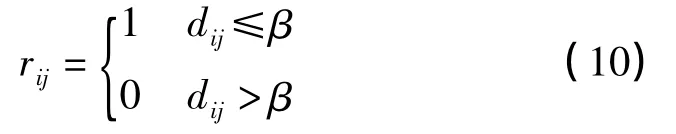
式中,β為常數。
分段型
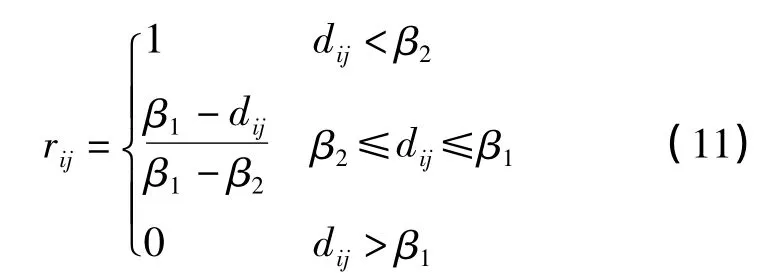
式中,β1、β2為常數,且β2<β1。
如下為幾種常見的支持度函數[7-8]
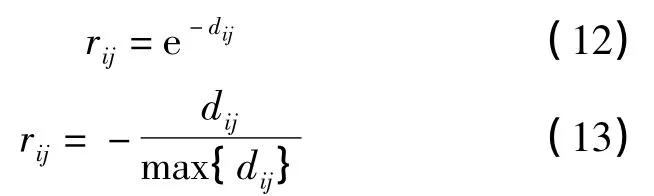
式中,i,j∈{1,2,…,m}。
選擇式(13)建立如下支持度矩陣
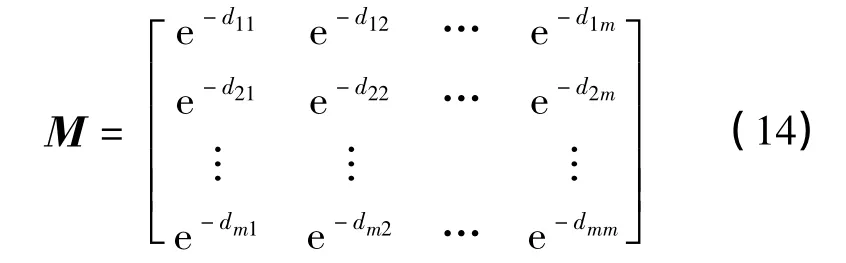
即


其矩陣形式為

式中,Η、Ν分別為由ωi和vj組成的列向量;Μ為非負對稱矩陣,存在最大模特征值λ;與其對應的特征向量為],量全為非負數。由特征向量特征值性質,可以取

融合后可以得到的預測值為
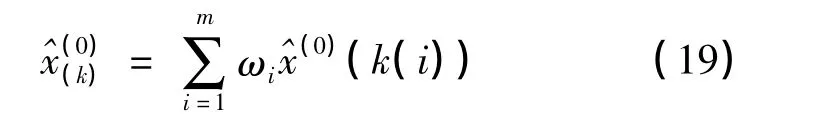
殘差為
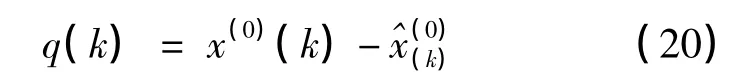
其相對誤差為

四、實例驗算
本文實例選用某滑坡沉降監測點1號點的位移時間序列數據[9]進行驗算。1~30期位移數據用于建模,31~48期位移數據進行預測計算,并與實測值比對,對預測結果進行精度評定,其結果如表1、圖1所示。
五、結 論
通過利用GM(1,1)預測模型并引用數據融合理論得到GM(1,1)數據融合預測算法,最后結合滑坡實例驗算,得出如下幾點結論。
1)由圖1可以看出,利用GM(1,1)模型作滑坡位移預測,由于自身誤差的不斷積累,導致長時距的預測結果越來越偏離實際;利用實際測量值不斷的迭代,對模型進行等維重建,可以促使模型不斷的自我修正;而后將不同維數時序數據建立的幾個GM(1,1)模型的預測值利用GM(1,1)數據融合算法進行預測值融合,就可以得到相對更好的結果,提高了預測精度。
2)表1中得到的GM(1,1)數據融合預測值是通過選取不等維的時序數據構造4個GM(1,1)模型,最后融合得到的預測值。在本文實例驗算中,筆者通過試驗發現構造4個GM(1,1)模型進行融合就可取得最優效果。對于其他滑坡的時間序列數據,構造多少個不等維GM(1,1)模型進行數據融合可以精度達到最高尚需進一步研究。
3)由圖1中時序38對應的預測數據可以看出,GM(1,1)數據融合預測模型的預測值偏差較大,預測的精度較低,對于某些突變的預測可能失效,尚需對模型進一步研究。
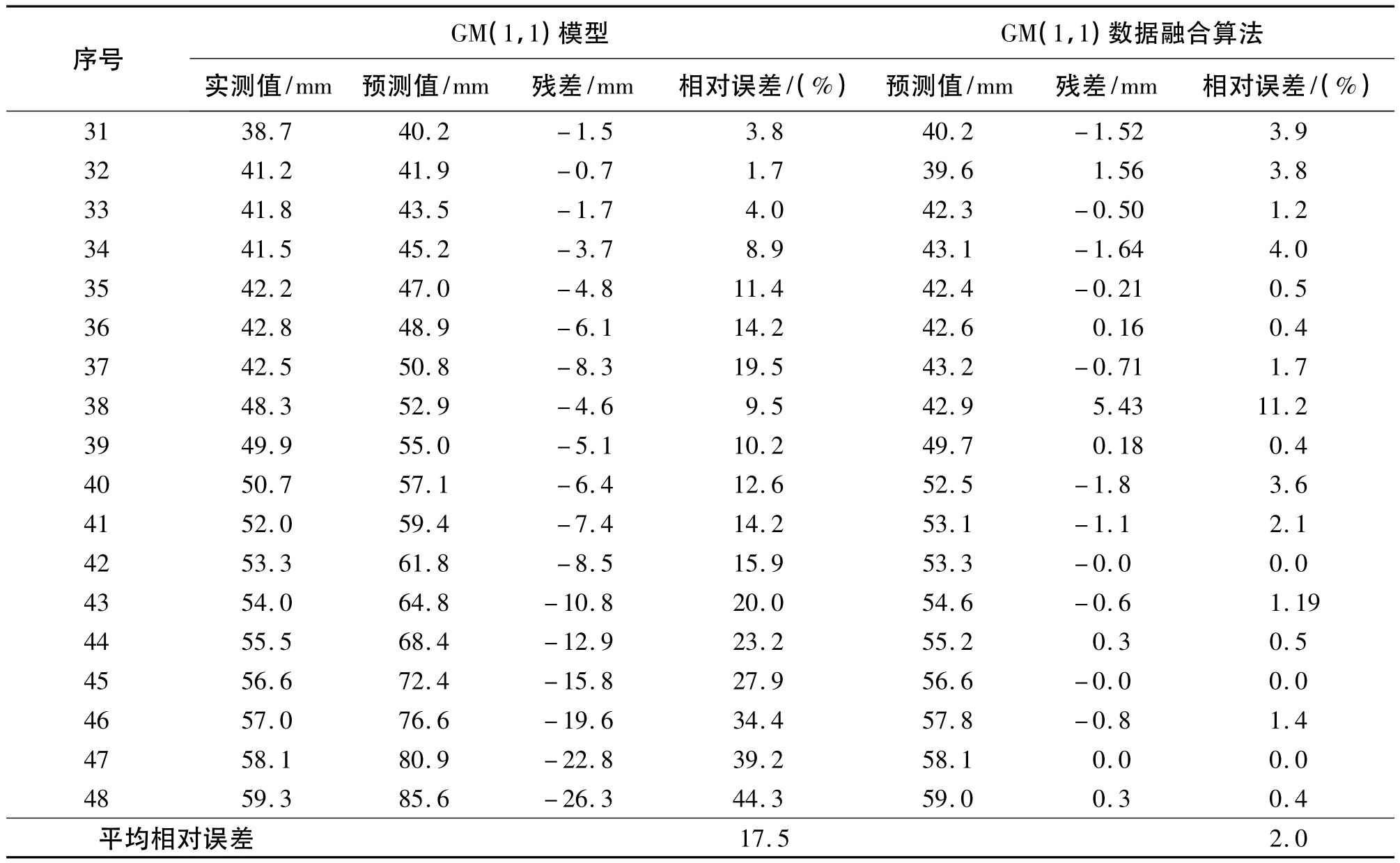
表1 GM(1,1)模型預測值與GM(1,1)數據融合模型預測值對比表
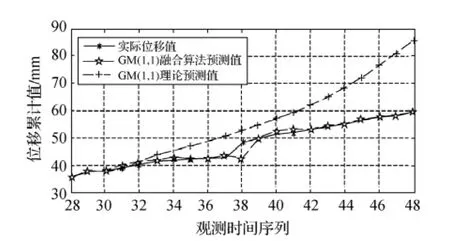
圖1 利用實測值迭代的融合結果與GM(1,1)理論預測值比對圖
[1] 李秀珍,許強.滑坡預報模型和預報判據[J].災害學,2003,18(4):71-78.
[2] 張華偉.數據融合算法研究及DSP實現[J].武漢理工大學學報,2009,31(3):84-86.
[3] 焦明連,蔣廷臣.基于GPS-InSAR集成技術地表形變的監測[J].測繪科學,2008,33(6):57-59.
[4] 尹暉.時空變形分析與預報的理論和方法[M].北京:測繪出版社,2002.
[5] 鄧聚龍.灰預測與灰決策[M].武漢:華中科技大學出版社,2000.
[6] 劉思峰,黨耀國,方志耕,等.灰色系統理論及其應用[M].3版.北京:科學出版社,2004.
[7] 高方偉,劉貴喜,王蕾,等.基于支持度矩陣的一種多傳感器融合方法[J].彈箭與制導學報,2007,27(4): 284-287.
[8] 胡振濤,劉先省.一種實用的數據融合算法[J].自動化儀表,2005,26(8):7-9.
[9] 張軍,劉祖強,鄧小川,等.滑坡監測分析預報的非線性理論和方法[M].北京:中國水利水電出版社,2010.
Research on Landslide Prediction Based on GM(1,1)Data Fusion Algorithm
WANG Tengjun,LAI Bailian,YE Junhua,YANG Zhiqiang
0494-0911(2012)05-0063-03
TU459
B
2012-03-09
王騰軍(1967—),男,河南淮陽人,副教授,主要研究方向為變形監測及預測預警。

