Banach空間中k-漸近擬偽壓縮映像不動點的迭代算法

陳東青，何斌，劉立紅

(軍械工程學院 基礎部，河北 石家莊 050003)

研究報告

Banach空間中k-漸近擬偽壓縮映像不動點的迭代算法

陳東青，何斌，劉立紅

(軍械工程學院 基礎部，河北 石家莊 050003)

在嚴格擬偽壓縮映像不動點的迭代算法基礎上，給出了Banach空間中漸近k-擬偽壓縮映像不動點的迭代算法，改進了算法，并證明了一個強收斂定理，擴展了已知的相關結果.

Banach空間；漸近k-擬偽壓縮映像；廣義投影算法；不動點

2010年，周海云和高興慧[1]給出了Banach空間中嚴格擬偽壓縮映像T不動點的迭代算法：

(1)

并且證明了下面的強收斂定理.

定理1 設X是自反的嚴格凸并且光滑的Banach空間，空間X及其對偶空間X*都具有性質(K)，C是X的非空閉凸子集.T：C→C為嚴格擬偽壓縮映像.{xn}由迭代格式(1)生成，其中k∈[0,1)，則序列{xn}強收斂到某一點p0=ΠF(T)(x0).

在文獻[1]的基礎上，引進K-漸近擬偽壓縮算子，并修正了迭代算法，證明了在自反的、嚴格凸、光滑的Banach空間中， 漸近擬偽壓縮映像不動點迭代算法的強收斂定理.

1 預備知識

J(x)={j∈X*:〈x,j〉=‖x‖2=‖j‖2},?x∈X.

(2)

注1[2]在自反的、光滑的Banach空間X中，J:X→2X*映像為單值的、次連續的滿值映像.

定義1[3]設X是實光滑的Banach空間，C是X的非空閉凸子集.定義泛函

?(x,y)=‖x‖2-2〈x,Jy〉+‖y‖2,x,y∈X.

根據?的定義，可以得到以下結論：

1)(‖x‖-‖y‖)2≤?(x,y)≤(‖x‖+‖y‖)2；

(3)

2)?(x,y)=?(x,z)+?(z,y)+2〈x-z,Jz-Jy〉.

(4)

定義2[1]設X是實自反、光滑、嚴格凸的Banach空間，C是X中的一個非空閉凸子集，廣義投影算子ΠC:x→C定義為：ΠC(x)={x0∈C:?(x0,x)=min(z,x),z∈C}.

當X=H為Hilbert空間時，ΠC=PC為H到C的距離投影算子.

注2 對于?x∈X，存在唯一的x0∈C，滿足?(x0,x)=min{?(z,x),z∈C}.

注3 若X是自反的嚴格凸且光滑的Banach空間，對于?x,y∈X，?(x,y)=0當且僅當x=y，并由此可得，〈x,Jy〉=‖x‖2=‖y‖2.

?(p,Tnx)≤kn?(p,x)+k?(x,Tnx).

(5)

當k=0時，T為漸近擬非擴張映像.

注4 關于性質(K)的更多內容，可詳見參考文獻[6].

引理1[7]設X是自反的嚴格凸且光滑的Banach空間，C是X中的非空閉凸子集，?x∈X，滿足 ?(y,ΠCx)+?(ΠCx,x)≤?(y,x),y∈C.

引理2[7]設X是自反的嚴格凸且光滑的Banach空間，C是X中的非空閉凸子集，x0∈C，x∈X,x0=ΠC(x)當且僅當〈x0-y,Jx-Jx0〉≥0,y∈C.

2 主要結果

定理2 設X是自反的嚴格凸且光滑的Banach空間，并且空間X和X*滿足性質(K)，C是X中的非空閉凸子集，T：C→C為閉的漸近k-擬偽壓縮映像,假設F(T)是有界的，且F(T)≠Φ，構造下列迭代算法：

(6)

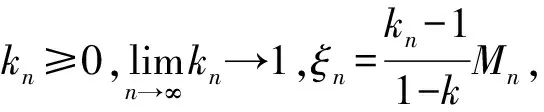
分7步完成定理的證明.

第1步：F是閉凸的.

首先，設序列{pn}?F(T)，且pn→p(n→∞)，由于T是k-漸近擬偽壓縮映像，故?(pn,Tnp)≤kn?(pn,p)+k?(p,Tnp).

再由式(4)得

?(pn,p)+?(p,Tnp)+2〈pn-p,Jp-JTnp〉≤kn?(pn,p)+k?(p,Tnp).

化簡可得

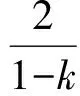
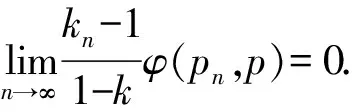
其次，?p1,p2∈F(T)，t∈(0,1).令pt=tp1+(1-t)p2，從而

?(p1,Tnpt)≤kn?(p1,pt)+k?(pt,Tnpt)，

以及

?(p2,Tnpt)≤kn?(p2,pt)+k?(pt,Tnpt).

再由式(5)，可得

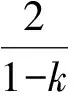
(7)

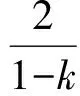
(8)

式(7)兩邊同時乘以t，式(8)兩邊同時乘以(1-t)，再相加可得

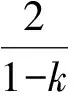
從而?(pt,Tnpt)→0(n→∞)，即Tnpt→pt(n→∞)，亦即Tn+1pt→pt(n→∞)，再由T的閉性得Tpt=pt，故F(T)是凸的.綜上所述，F(T)是閉凸的.

第2步：?n≥1，Cn是閉凸的.

事實上當n=1時，Cn=C，即C1是閉凸的.假設Cn-1是閉凸的，需要證明Cn是閉凸的.

注意到Cn是Cn-1與一個閉凸集的交，故Cn是閉凸的.

根據歸納法可知，Cn是閉凸的(重復).

第3步：F?Cn.

顯然F?C=C1，假設F?Cn,下證F?Cn+1.對于?p′∈F，p′∈Cn.再由T是k-漸近擬偽壓縮映像，從而

?(p′,Tnxn)≤kn?(p′,xn)+k?(xn,Tnxn).

(9)

再結合式(4)可得

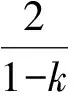
于是p′∈Cn+1，即F?Cn+1，根據數學歸納法可得F?Cn，因而ΠCn(x0)有意義，從而序列{xn}可由式(6)生成.

由xn=ΠCn(x0)可得〈xn-z,Jx0-JXn〉≥0，?z∈Cn,?n≥1.并且F?Cn，?p∈F，有〈xn-p,Jx0-Jxn〉≥0,?z∈Cn.再由引理1，得

?(xn,x0)=?(ΠCnx0,x0)≤?(p,x0)-?(p,xn)≤?(p,x0),

(10)

故?(xn,x0)是有界的.

另一方面，xn=ΠCn(x0)，xn+1=ΠCn+1(x0)∈Cn，Cn+1?Cn，可知?(xn,x0)≤?(xn+1,x0).

(11)

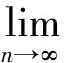
第5步：xn→p0(n→∞).

由Cn的構造可知，xn+1=ΠCn+1(x0)∈Cn+1?Cn，據引理1得

?(xn+1,xn)≤?(xn+1,ΠCn+1x0)≤?(xn+1,x0)-?(ΠCnx0,x0)=?(xn+1,x0)-?(xn,x0).

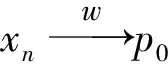
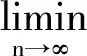
故?(xn,x0)→?(p0,x0)(n→∞)，于是‖xn‖→‖p0‖.由空間X滿足性質(K)，知xn→p0(n→∞) .

第6步：p0=Tp0.

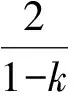
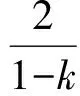
整理得

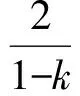
(12)

由第4步可知序列{xn}是有界的，從而由式(12)可得{‖Tnxn‖}也是有界的.

由xn+1∈Cn+1，可得

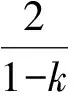
(13)

由第5步可知?(xn+1,xn)→0，對式(13)兩邊同時取極限可得

?(xn,Tnxn)→0(n→∞).

(14)

注意到0≤(‖xn‖-‖Tnxn‖)2≤?(xn,Tnxn).因此‖Tnxn‖→‖p0‖，并且‖J(Tnxn)‖→‖Jp0‖，故{J(Tnxn)}是有界的.由于X是自反的，故X*也是自反的.因此，可以假設

另一方面，由于X是自反的，從而J(X)=X*，即對于f0∈X*，?x∈X，使得Jx=f0.

于是?(xn,Tnxn)=‖xn‖2-2〈xn,JTnxn〉+‖Tnxn‖)2=‖xn‖)2-2〈xn,JTnxn〉+‖JTnxn‖2.等號兩邊同時取下極限，有0≥‖p0‖2-2〈p0,f0〉+‖f0‖2=‖p0‖2-2〈p0,Jx〉+‖Jx‖2=?(p0,x)≥0.

故?(p0,x)=0，從而p0=x，即f0=Jp0.因此

(15)

又由‖J(Tnxn)‖→‖Jp0‖，由X*具有性質(K)知‖J(Tnxn)-Jp0‖→0.

注意到J-1:X*→X是次連續的，于是有

(16)

又由‖Tnxn‖→‖p0‖，并且空間X滿足性質(K)，可得Tnxn→p0(n→∞).因為xn→p0，并且T是閉的，故有p0=Tp0.

(17)

第7步：p0=ΠF(T)(x0).

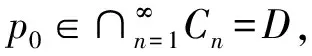
從第5步和第6步可知，?(p0,x0)≤?(ΠFx0,x0)≤?(p0,x0)，從而

?(ΠF(T)x0,x0)=?(p0,x0).

(18)

因此ΠF(T)x0=p0，于是由式(6)生成的序列{xn}強收斂到p0=ΠF(T)(x0).

定理得證.

[1] ZHOU Haiyun,GAO Xinghui.An iterative method of fixed points for closed and quasi-strict pseudo-contraction in Banach spaces [J].J Appl Math Comput, 2010, 33:227-237.

[2] TAKAHASHI W. Nonlinear functional analysis [M].Yokohama:Yokohama Publishers, 2000.

[3] CARLOS M Y, XU Hongkun.Strong convergence of the CQ method for fixed point iteration processes [J]. Nonlinear Anal, 2006, 64:2400-2411.

[4] KAMIMURA S, TAKAHASHI W. Strong convergence of a solution to accretive operator inclusions and applications [J].Set-Val-ue Anal，2000, 8:361-374.

[5] QIN Xiaolong. On the convergence of iterative processes for nonlinear operators [D]. Chinju:Gyeongsang National University, 2010.

[6] HUDZIK H, KOWALEWSKI W, LEWICKI G. Approximative compactness and full rotundity in Musielak-Orlicz spaces and Lorentz-Orlicz spaces [J].Z Anal Anwend, 2006,25:163-192.

[7] ALBER, YA I.Metric and generalized projection operators in Banach spaces [M].New York:Marcel Dekker, 1996.

[8] ZHOU Haiyun, GAO Gailiang, TAN Bin. Convergence theorems of a modified hybrid algorithm for a family of quasi-asymptotically nonresponsive [J].J Appl Math Comput, 2010,32:453-464.

(責任編輯：王蘭英)

Iterationmethodforfixedpointsofasymptoticallyquasipseudo-contractionmappinginBanachspaces

CHENDong-qing,HEBin，LIULi-hong

(Department of Basic Courses, Ordnance Engineering College, Shijiazhuang 050003, China)

Based on the iteration method for fixed points of quasi-strict psedo-contraction mapping, an iteration algorithm for fixed points ofk-asymptotically quasi pseudo-contraction mapping in Banach spaces is proposed, then a strong convergence theorem is proved by using the modified algorithm. The known related results are extended.

Banach spaces;k-asymptotically quasi pseudo-contraction mapping; generalized hybrid projection; fixed point

O177.91

A

1000-1565(2012)02-0113-05

2011-09-10

國家自然科學基金資助項目(11071053)；軍械工程學院基金項目(YJJXM11003)

陳東青(1962-)，男，遼寧錦縣人，軍械工程學院副教授，主要從事非線性泛函分析研究.

E-mail：liulihong2003@sohu.com

MSC201047H05;47H10;47H17