多機并網發電系統孤島效應的檢測方法

孫 強， 段 凱

(西安理工大學自動化與信息工程學院， 西安 710048)

多機并網發電系統孤島效應的檢測方法

孫 強， 段 凱

(西安理工大學自動化與信息工程學院， 西安 710048)

當分布式發電系統接入公共電網時，孤島檢測是其必備的重要功能。目前的研究主要集中在單機，而該文從多機并網運行的角度對孤島檢測方法進行了研究。文中將小波變換技術引入到孤島檢測當中，運用Mallat算法對采集信號進行多尺度分析，通過信號低頻系數的變化進行孤島檢測。從不同數量逆變器與不同品質因數負載的角度對本方法作了仿真驗證，結果證明其能有效檢測出孤島，且非檢測區小，對電網無干擾。

分布式發電系統； 并網； 多機； 孤島檢測

隨著大量分布式發電系統的并網運行，一系列電能質量問題顯現出來，其中尤為重要的是孤島效應問題。

“孤島”是指公共電網停止供電后，由于分布式發電系統的存在(與電網相連并輸送電能)，使電網停電區的部分線路仍維持帶電狀態，形成自給電力供應的島狀區域[1]。在孤島狀態下電力公司失去對線路電壓、頻率的控制，會帶來一系列的安全隱患及事故糾紛[2]。

本文將小波變換技術引入到孤島檢測中，運用Mallat算法對采集信號進行多尺度分析，通過信號低頻系數的變化進行孤島檢測。在多機并網系統中作了仿真驗證，結果證明該方法準確、有效。

1 小波變換的基本原理

設δ∈L1∩L2，且滿足容許度條件

(1)

則信號x(t)的連續小波變換可定義為

(2)

而且

(3)

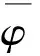
(4)

式中：k為離散時間參數；m和n分別為二進離散小波的尺度因子和位移因子。式(4)相當于信號x(t)通過了一傳遞函數為φ(ω)的帶通濾波器。不同的m值，就相當于信號通過了不同的帶通濾波器。這樣就可以把不同頻帶的信號分離開來[3，4]。

2 基于Mallat算法的孤島檢測方法

2.1Mallat算法

Mallat基于多分辨率分析框架，建立了小波快速算法-Mallat算法[5]。Mallat算法把小波函數的構造歸結為濾波器系數的設計，從而實現了離散小波變換的高效算法。

假定非平穩信號x(t)在零尺度下的離散逼近c0(n)為已知，并且可以用對該信號的采樣序列x(n)來近似代替，即

c0(n)=x(n)n=0，1，…，S-1

(5)

式中，S=2J，J∈N(自然數集)。序列c0(n)可以分解為一小波系數序列d1(n)和一逼近系數序列c1(n)。對后者進行同樣的分解又可得一新的小波系數序列和逼近系數序列。前者含有信號中較高的頻率成分，而后者則含有信號中較低的頻率成分。信號中不同頻帶的分量被分離，從而能夠更好地分析和提取信號特征。

2.2 孤島檢測方法

選擇合適的小波是測量準確、可靠的重要保證。如小波能夠保證正交性，可在一定程度上避免因小波變換之間的關聯而造成分析變換結果困難的問題；為了檢測信號中的突變點，所選擇的小波必須很正則(有規則)，這時的小波可實現一個更長的沖擊響應濾波器。本文采用了正則性較好的Discrete Meyer wavelet(Dmey)小波對信號進行分解，觀察其低頻系數變化定位孤島效應的發生。

3 基于小波變換的多機并網孤島檢測

隨著大量分布式發電系統的并網運行，多機狀態下的孤島檢測成為一個重要的研究課題[6，7]。本文以多逆變器并網系統為例，分以下兩種情況來討論孤島檢測的有效性：①相同品質因數負載，不同數量逆變器情況下的孤島檢測；②相同數量逆變器，不同品質因數負載情況下的孤島檢測。

3.1 不同數量逆變器情況下的孤島檢測

選擇負載參數為R=211.6 Ω，L=269.4×10-3H，C=37.6×10-6F。分別研究單機與多機情況下的孤島檢測性能。

1)單機并網系統

用于孤島問題研究的逆變器并網系統結構如圖1所示[8]。

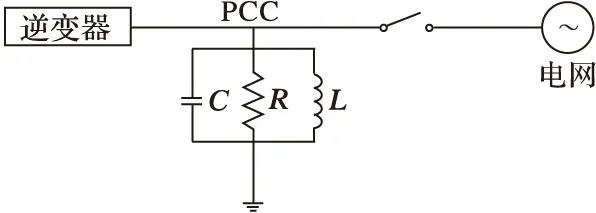
圖1 用于孤島問題研究的逆變器并網系統結構

孤島發生時電網側電流如圖2所示。

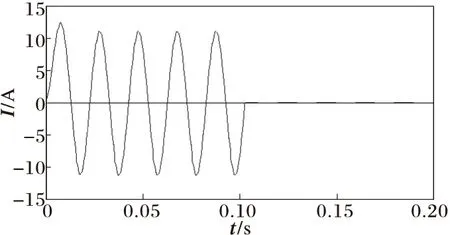
圖2 孤島發生時電網側電流波形

當逆變器輸出有功與負載需求平衡時，本地負載電流波形如圖3所示。

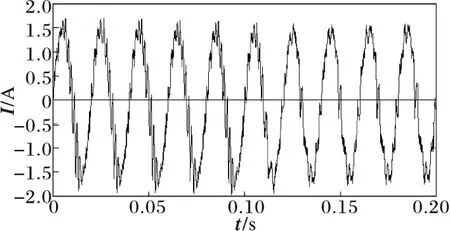
圖3 本地負載電流波形

對本地負載電流作小波變換，負載電流小波變換第十二層低頻系數如圖4所示。分析分解的結果，當孤島發生時，低頻系數發生了明顯的變化。

2)多機并網系統

多逆變器并網系統結構如圖5所示[9，10]。為了便于仿真，本文以四逆變器并網系統為例進行討論，其中，各逆變器負載取值相同。

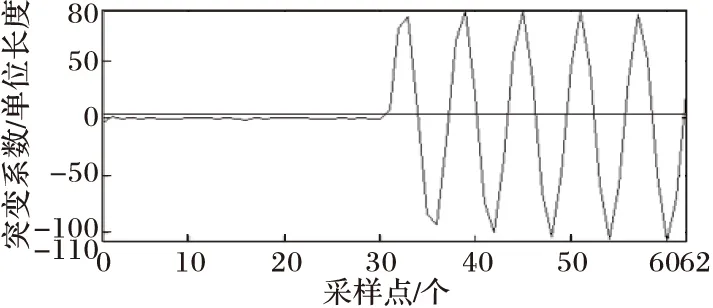
圖4 負載電流小波變換低頻系數

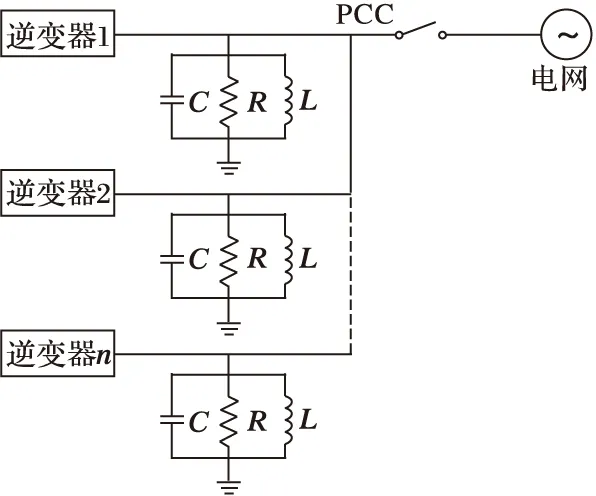
圖5 多逆變器并網系統結構

本地負載電流波形如圖6所示。對其作小波變換，第十二層低頻系數如圖7所示。可以看到低頻系數的變化準確對應著孤島發生的時刻。

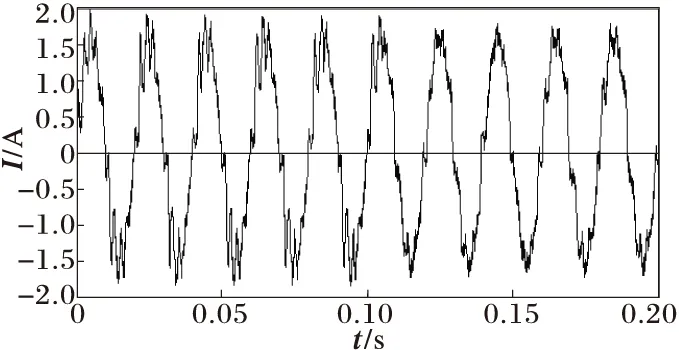
圖6 本地負載電流波形

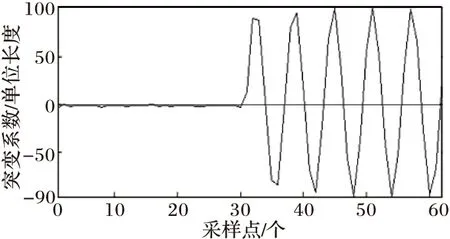
圖7 負載電流小波變換低頻系數

3.2 不同品質因數負載情況下的孤島檢測

本文以兩臺逆變器并網系統為例，研究不同品質因數負載情況下的孤島檢測性能，取負載的諧振頻率等于電網頻率，逆變器輸出有功與負載需求平衡，其中各逆變器負載取值相同。

當Q=0.5時，取負載參數為R=211.6 Ω，L=1.3 H，C=7.3×10-6F，即大電感、小電容負載。此時，負載電流及相應的低頻系數如圖8所示。

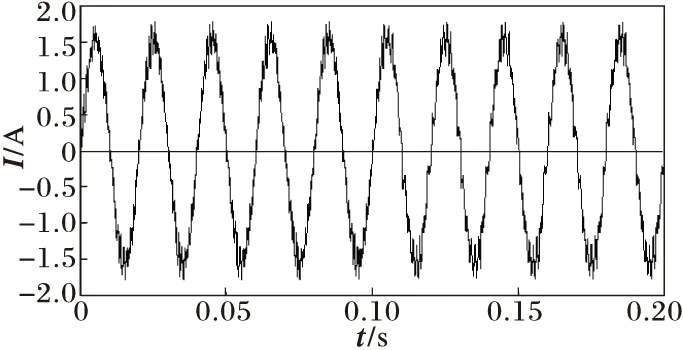
(a) 本地負載電流波形

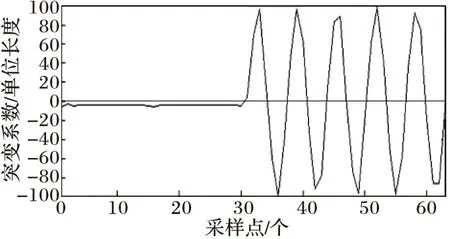
(b) 負載電流低頻系數

當Q=2.5時，取負載參數為R=211.6 Ω，L=269.4×10-3H，C=37.6×10-6F，即常用平衡負載。此時，負載電流及相應的低頻系數如圖9所示。

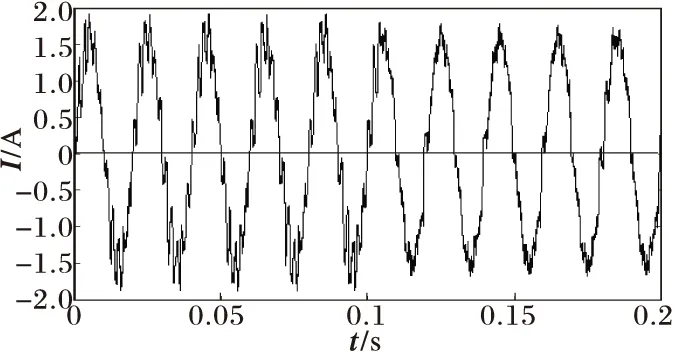
(a) 本地負載電流波形

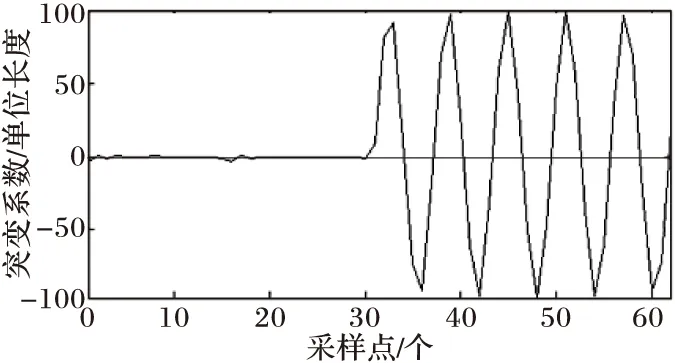
(b) 負載電流低頻系數

當Q=10.0時，取負載參數為R=211.6 Ω，L= 67.4×10-3H，C= 150.4×10-6F，即小電感、大電容負載。此時，負載電流及相應的低頻系數如圖10所示。

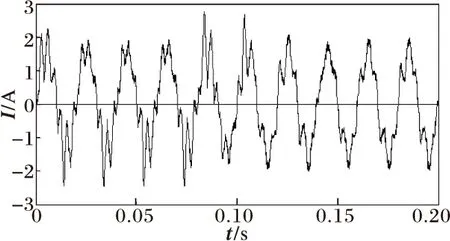
(a) 本地負載電流波形

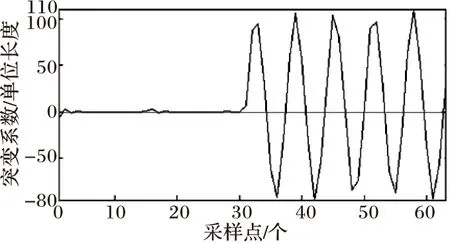
(b) 負載電流低頻系數

對以上仿真結果進行分析，可以看出在各種品質因數負載情況下，本方法均能準確檢測出孤島現象的發生，故非檢測區較小。

4 結語

本文對多臺分布式發電系統并聯運行時的孤島效應檢測進行研究，引入基于小波變換技術的方法。該孤島檢測方法非檢測區小，不會因為多機使用而互相削弱。同時，該方法對電網無干擾，輸出電能質量高。綜合考慮該性能及對電能質量的影響，基于小波變換的孤島檢測將是未來發展的方向。

[1] 曾議, 吳政球, 劉楊華, 等(Zeng Yi, Wu Zhengqiu, Liu Yanghua,etal). 分布式發電系統孤島檢測技術(Islanding detection method for distributed generation systems)[J].電力系統及其自動化學報(Proceedings of the CSU-EPSA)，2009，21(3)：106-110.

[2] Ropp M, Ginn J, Stevens J,etal. Simulation and experimental study of the impedance detection anti-islanding method in the single-inverter case[C]∥IEEE 4th World Conference on Photovoltaic Energy Conversion, Waikoloa, USA: 2006.

[3] Daubechies I. Ten Lectures on Wavelets[M]. Philadelphia, Pennsylvania: SIAM Mathematical Analysis, 1992.

[4] 秦前清，楊宗凱. 實用小波分析[M]. 西安：西安電子科技大學出版社，1994.

[5] Mallat S G. Theory for multiresolution signal decomposition: the wavelet representation[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 1989, 11(7):674-693.

[6] Yu Byunggyu , Matsui Mikihiko, Yu Gwonjong . A review of current anti-islanding methods for photovoltaic power system[J]. Solar Energy, 2010, 84(5):745-754.

[7] 劉方銳，余蜜，張宇，等(Liu Fangrui, Yu Mi, Zhang Yu,etal).主動移頻法在光伏并網逆變器并聯運行下的孤島檢測機理研究(Islanding detection evaluation for active frequency drifting methods in multiple photovoltaic grid-connected converters)[J].中國電機工程學報(Proceedings of the CSEE)，2009, 29(12):47-51.

[8] 張純江，郭忠南，孟慧英，等(Zhang Chunjiang, Guo Zhongnan, Meng Huiying,etal).主動電流擾動法在并網發電系統孤島檢測中的應用(Active current disturbing method for islanding detection of grid-connected inverters)[J].電工技術學報(Transactions of China Electrotechnical Society)，2007, 22(7):176-180.

[9] 程軍照, 李澍森, 張騰飛(Cheng Junzhao, Li Shusen, Zhang Tengfei).多路并網光伏發電系統的仿真與分析(Simulations and analysis on a multi-branch grid-connected photovoltaic system)[J].電力系統及其自動化學報(Proceedings of the CSU-EPSA)，2009，21(4)：58-62.

[10]Doumbia Mamadou Lamine, Agbossou Kodjo, Viet Dung Tran Khanh. Correlation technique investigation for islanding detection of inverter based distributed generation[C]// IEEE Annual Power Electronics Specialists Conference, Rhodes Greece: 2008.

孫 強(1955-)，男，教授，研究方向為大功率高頻高壓開關電源及特種工業電源、現代高效功率變換器理論與應用、先進控制與自動化裝備。Email:sq@xaut.edu.cn

段 凱(1986-)，男，碩士研究生，研究方向為自動化裝置及其檢測技術、電力電子與新能源發電技術。

DetectionMethodofIslandingforMultipleGrid-connectedGenerationsSystem

SUN Qiang， DUAN Kai

(School of Automation and Information Engineering， Xi'an University of Technology， Xi'an 710048， China)

When distributed generation systems are connected to the public power grid, the function of islanding detection is necessary. The current research is mainly focusing on islanding detection for single generation system. This paper is dedicated to investigate the strategies for multiple grid-connected generation operation. This article introduces the technique of islanding detection based on wavelet transform, Mallat algorithm is used for multi-resolution analysis of collected signals, and the islanding is detected by changes on signal coefficients of approximation. Simulations are made on aspects of different number of inverters and different quality factors of loads. The results verify that the proposed method not only can identify the islanding very well, but also has a tiny non-detection zone and no impact on systems.

distributed generation system； grid-connected； multiple generations system； islanding detection

TM464

A

1003-8930(2012)05-0063-04

2010-11-30；

2011-01-17