奇異值分解降噪的改進方法

張 磊 彭偉才 原春暉 劉 彥

中國艦船研究設計中心船舶振動噪聲重點實驗室，湖北武漢 430064

0 引 言

在船舶振動噪聲信號的測試過程中，總存在著由現場測試環境及儀器本身產生的誤差源［1-4］，其中一個不可避免的誤差源就是隨機噪聲。測量信號中的噪聲水平直接決定了分析的可靠性，為此，必須消除或者最小化信號中的噪聲干擾。

作為信號降噪的有效方法之一，奇異值分解（SVD）已被廣泛應用于許多工程領域，如信號濾波和矩陣秩的估計。將受到噪聲污染的信號構造成Hankel矩陣，然后對其進行奇異值分解，將包含信號特征的矩陣分解到一系列奇異值和奇異值矢量對應的子空間中，是對Hankel矩陣進行噪聲過濾的一種非線性濾波方法。從SVD降噪的基本原理來看，其關鍵就是確定Hankel矩陣的有效奇異值數目，奇異值數目選擇不當，會極大地影響降噪效果。而目前用于確定奇異值數目的方法，如奇異值曲線、奇異熵增量［5］、信噪比經驗［6］等，都不能明確地給出有效階次，往往只能依靠經驗選取。

本文將通過仿真分析與實驗測試來研究奇異值數目變化時噪聲對信號的干擾影響。

1 奇異值分解降噪基本原理

對于一個受噪聲污染的離散信號 X={x1，x2，…，xL}，構造成m×n(m≤n)維的Hankel矩陣為：

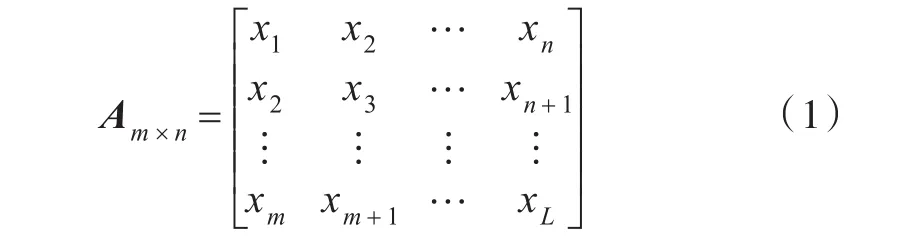
式中，A為Hankel矩陣；m為嵌入維數，并且滿足m+n-1=L。

對Hankel矩陣進行奇異值分解可得到：

式中，U為m×m維正交矩陣；V為n×n維正交矩陣；Σ為m×n維矩陣。主對角元素為矩陣的奇異值，并且從大到小排列。

矩陣A為由受噪聲污染的信號構成的Hankel矩陣，可以表示為未受噪聲污染的信號子空間和噪聲子空間之和：

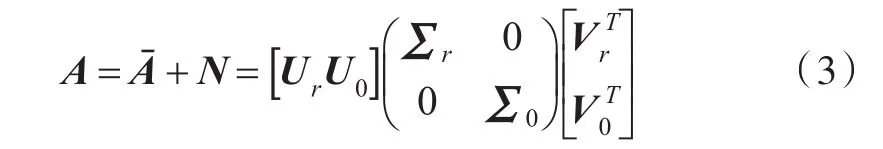
保留對角矩陣的前k個有效奇異值，將其他的奇異值設置為零，利用奇異值分解的逆過程得到重構矩陣。一般來說，這時的重構矩陣不再是Hankel矩陣的形式。為了得到降噪后的信號，需要對重構矩陣中的反對角元素采用下式進行平均：

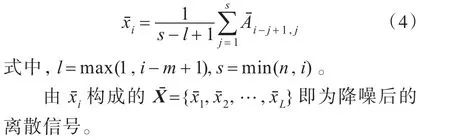
2 改進方法

由實測經驗可知，當實際測量環境很好時，測量得到的信號一般為光滑曲線；而當受到外界的隨機噪聲干擾時，測量得到的信號中就會含有大量的“毛刺”。

利用噪聲污染信號構造Hankel矩陣進行奇異值分解降噪，就是對含噪信號進行逼近、剔除毛刺的過程。經過對大量仿真結果的研究，發現去噪結果中剩余噪聲對信號的干擾影響能夠通過信號中“毛刺”的數量及大小來判斷，這與實測經驗相吻合。當選取的奇異值數目較小時，大部分噪聲都被剔除掉了，但也損失了大量有用信號。隨著奇異值數目的逐漸增大，有用信號信息趨于完整，但噪聲的干擾也會逐漸增加。當奇異值數目達到某一值時，降噪后的信號既保留了大部分有用信息，也剔除掉了大部分噪聲，這就是要選取的最佳奇異值數目。當奇異值數目再增加時，基于隨機噪聲對信號干擾的特點，降噪后的信號中會出現大量“毛刺”，波動明顯，在數學意義上可表示為有大量極值點出現。本文根據降噪后信號極值點（均指極大值點）數量的變化，找到了突變點，可清晰地判斷應該選取的有效奇異值數目。

本文信噪比計算所用的公式為：

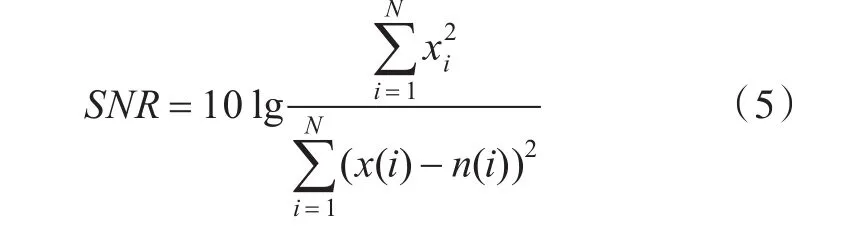
式中，SNR為信噪比，dB；n(i)為含有噪聲的信號；x(i)為真實信號；N為信號長度。

3 仿真分析

3.1 噪聲干擾對奇異值的影響

經過對無噪聲理想信號和受噪聲污染信號的研究，發現一般由無噪聲理想信號構造的Hankel矩陣的大部分奇異值為零。根據非零奇異值的數目，可以很容易地判斷矩陣的有效階次。因噪聲具有隨機和不相關的特點，因此，由受隨機噪聲污染信號構造的Hankel矩陣呈列滿秩或行滿秩狀態（取決于行和列哪個維數更小）。

現取如圖1所示的無噪聲理想信號和噪聲污染信號進行仿真分析。無噪聲理想信號clean signal＝sin（3×t）＋sin（5×t）＋sin（8×t），單位為 V，其中 t為時間間隔為0.01的從0～2變化的時間序列。在無噪聲理想信號中加入信噪比約為6dB（通過式（5）計算得到）的高斯白噪聲，得到了圖1中的噪聲污染信號，噪聲干擾明顯。

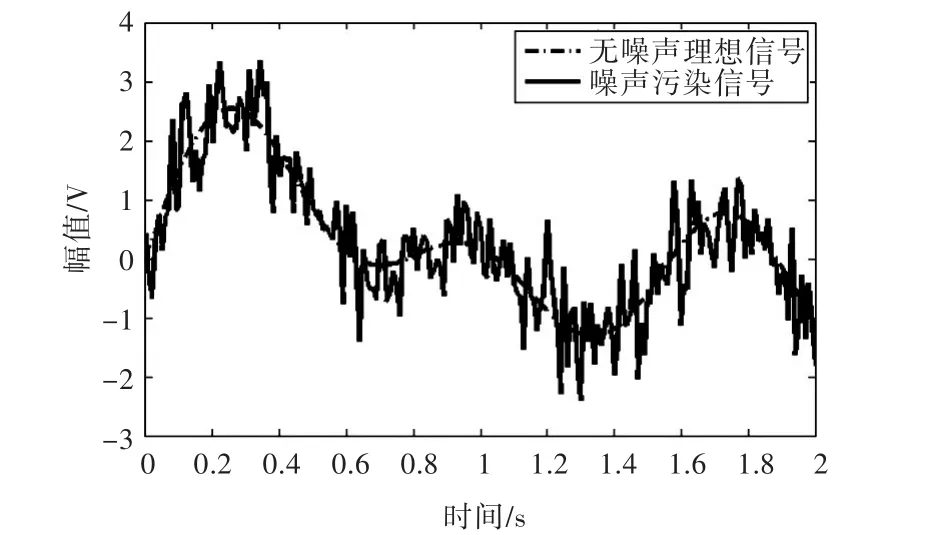
圖1 無噪聲理想信號與噪聲污染信號Fig.1 Clean signal and noisy signal

對圖1中的兩個信號取維數m＝80，n＝122構造Hankel矩陣（本文在此不討論如何選取的維數，具體方法可參考文獻［8］），進行奇異值分解，得到奇異值序列圖如圖2所示（只顯示了80個奇異值中的前30個）。

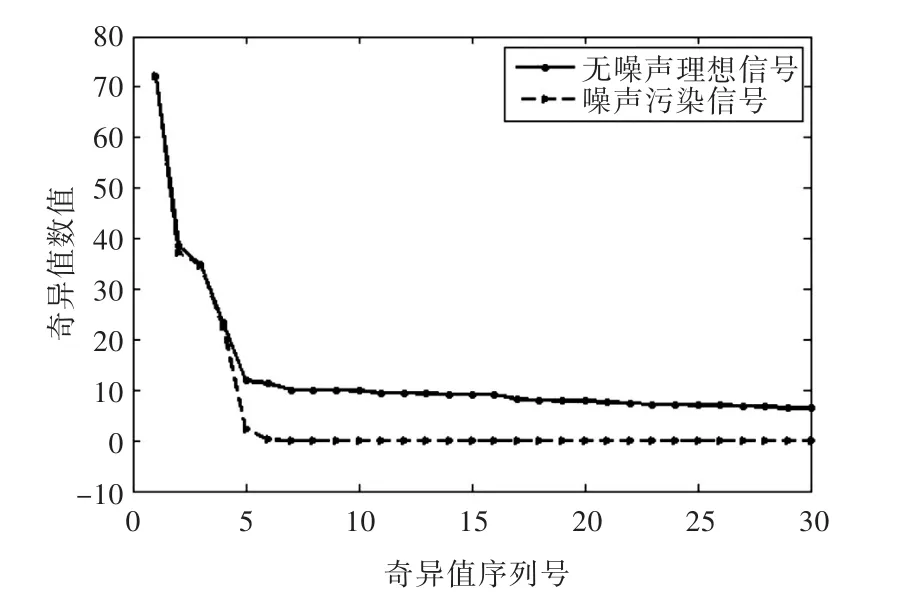
圖2 無噪聲理想信號和噪聲污染信號的奇異值序列圖Fig.2 Singular value curves of clean signal and noisy signal

對比圖2中的兩條奇異值曲線可知，每個奇異值受到噪聲干擾的程度不同：較大的奇異值受噪聲干擾的影響較小，而較小的奇異值受噪聲干擾的影響則較大。由于由受噪聲污染信號構造的Hankel矩陣的每個奇異值都是由“有用信號”和“噪聲信號”兩部分組成，實際選取奇異值數目就是一個對有用信號和噪聲信號進行取舍的過程，所以，就要考慮在所選取的數目對應的那個奇異值中，有用信號和噪聲信號的比例關系。

3.2 方法對比

3.2.1 奇異值曲線和奇異熵增量

奇異值曲線和奇異熵增量判斷有效奇異值數目的方法，分別是以奇異值擬合曲線和奇異熵增量曲線的拐點來作為閾值設置的依據。實際計算結果表明，兩種曲線除幅值有所變化外，形狀并沒有多大區別。

對圖1中受噪聲污染的信號取維數m＝80，n＝122構造Hankel矩陣，進行奇異值分解，得到奇異值序列圖（圖3）和奇異熵增量隨奇異值數目變化的曲線圖（圖4）。通過對比，證實上述結論是正確的。

由于降噪效果往往對奇異值的數目很敏感，因此，奇異值數目的微小差別都將導致信號去噪效果有較大差異。上述方法存在的主要問題就是拐點不夠清晰，即使存在拐點，選取對應的奇異值數目一般也不能得到最優的降噪結果。采用上述兩種方法，并通過觀察圖3和圖4，可以選取奇異值的數目為5。

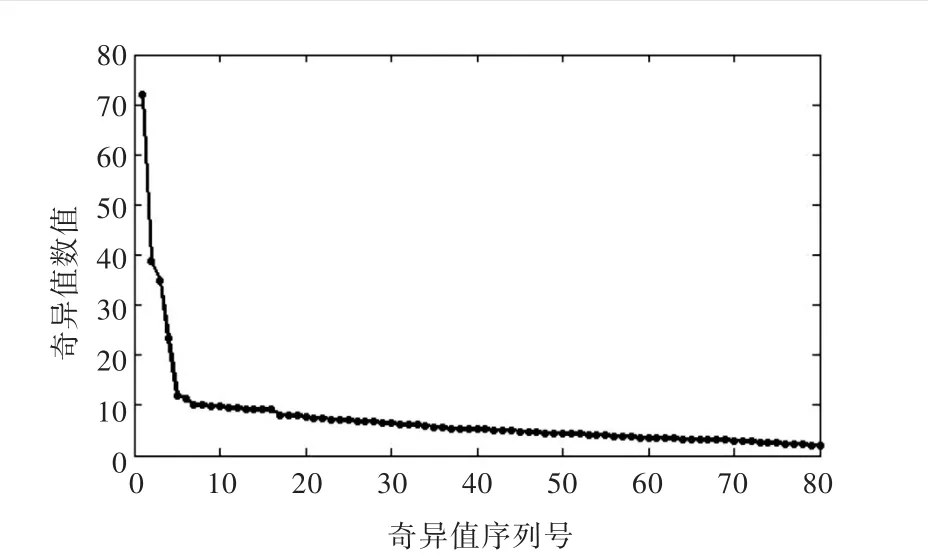
圖3 奇異值序列圖（噪聲污染仿真信號）Fig.3 Singular value curve（noisy simulation signal）

圖4 奇異熵增量隨奇異值數目變化的曲線圖（噪聲污染仿真信號）Fig.4 Increment of the singularity entropy versus the number of the singular values（noisy simulation signal）

當選取的奇異值數目為5時，通過計算，得到降噪后的信噪比為18.5 dB。去噪后的信號與無噪聲理想信號的對比如圖5所示。由圖可見，信號中含有很多“毛刺”，尤其是后半段受噪聲影響較嚴重。

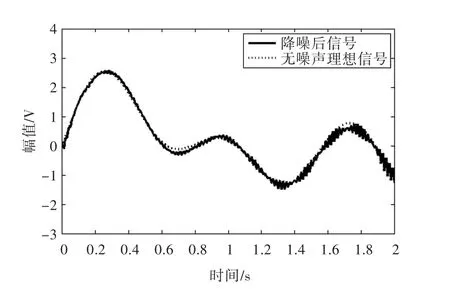
圖5 奇異值數目為5對應的降噪信號和無噪聲理想信號Fig.5 Noise elimination signal with 5 singular values and clean signal

3.2.2 改進方法——極值點數量

現利用改進的方法，采用與第3.2.1小節中相同的維數構造Hankel矩陣，進行奇異值分解。通過計算得到的信號降噪后極值點數量隨選取奇異值數目變化的關系如圖6所示。極值點數量突變非常明顯，要選取的有效奇異值數目為4。

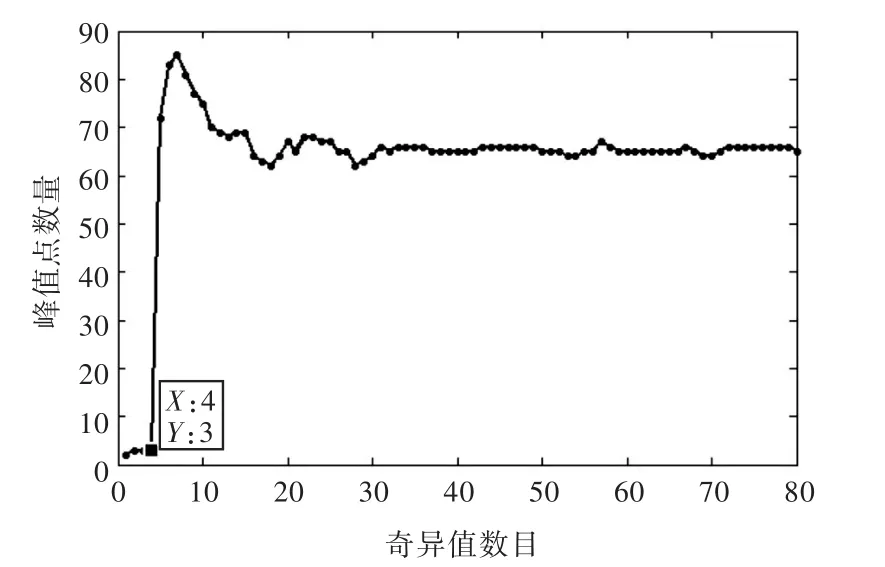
圖6 極值點數量隨奇異值數目變化圖（噪聲污染仿真信號）Fig.6 Number of the extremum points versus the number of singular values（noisy simulation signal）

當奇異值數目為4時，通過計算得到降噪后的信噪比為 22.3 dB，相比第 3.2.1小節中用兩種方法選取奇異值數目為5時的信噪比（18.5 dB），有明顯的提高。降噪信號和無噪聲理想信號的對比如圖7所示。由圖可見，其明顯優于圖5中的降噪效果。

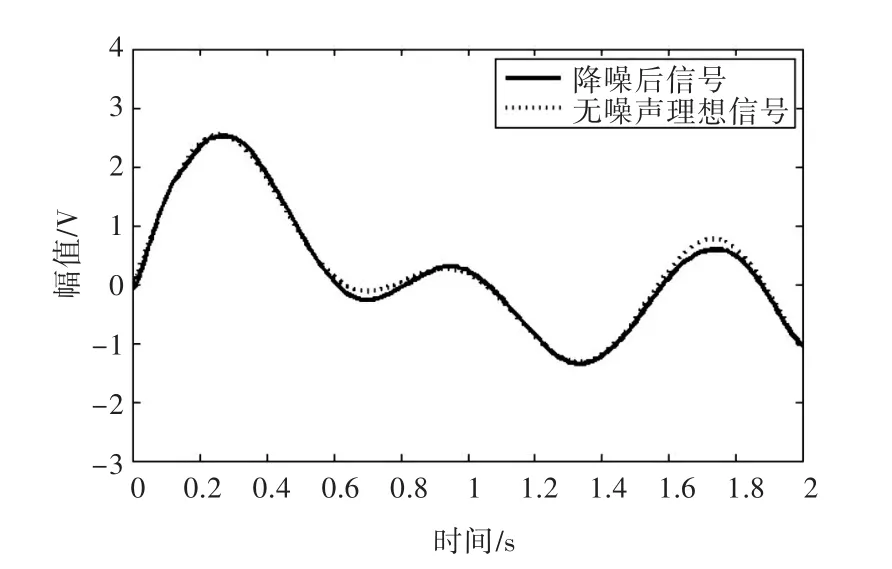
圖7 奇異值數目為4對應的降噪信號和無噪聲理想信號Fig.7 Noise elimination signal with 4 singular values and clean signal

當奇異值數目小于最佳的選項4時，為使效果更明顯，例如，選取1時，其降噪后的信噪比為6.3 dB，相比奇異值數目為 4時的信噪比 22.3 dB，有較大的衰減。去噪后的信號與無噪聲理想信號的對比如圖8所示。由圖可見，降噪信號中沒有“毛刺”，但形狀有明顯的改變，第2和第3個峰值已基本被過濾掉。

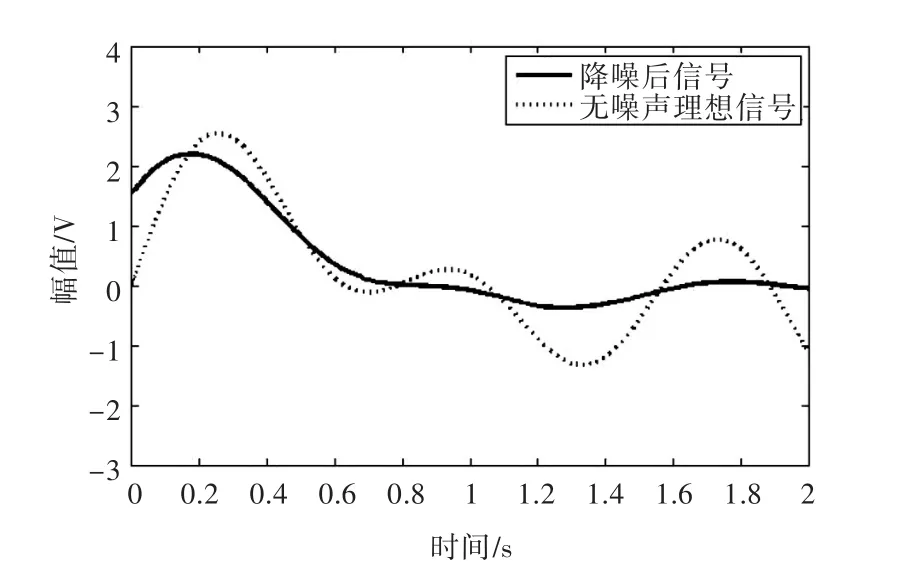
圖8 奇異值數目為1對應的降噪信號和無噪聲理想信號Fig.8 Noise elimination signal with 1 singular value and clean signal

圖9所示為奇異值數目從1～8變化時信號降噪后的信噪比曲線圖。由圖可見，奇異值數目為4時，信噪比最高；當奇異值數目大于或者小于4時，信噪比都有所下降，故4為最優選擇。

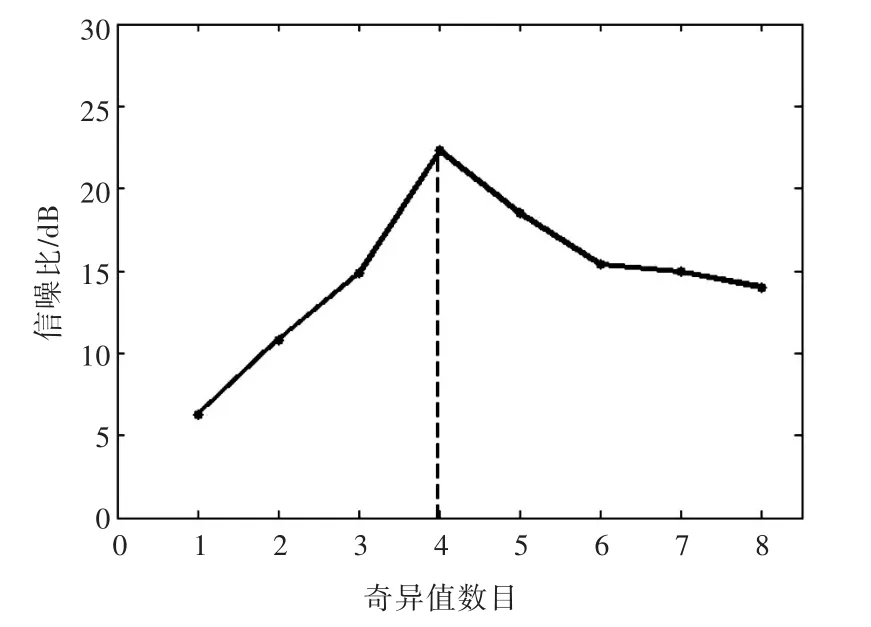
圖9 降噪信號信噪比隨選取奇異值數目變化的曲線圖（噪聲污染仿真信號）Fig.9 Signal to noise ratio versus the number of the singular values（noisy simulation signal）

綜上所述，Hankel矩陣有效奇異值數目的確定至關重要，選取不當，就會造成結果偏差較大。當奇異值數目選取過小時，因奇異值的組成中主要是有用信號，噪聲的干擾可以忽略不計，所以降噪后的信號中沒有噪聲引起的明顯波動。但由于閾值選取過大，很多包含在奇異值中的有用信號也被剔除掉了，表現為有用信號的損失。當選取最佳的奇異值數目時，不僅過濾掉了大量的噪聲，而且還最大程度地保留了原始信號的信息，與原始信號吻合很好。所以，在降噪后剩余噪聲對信號沒有明顯影響的情況下，選取的奇異值數目越大，信噪比越高，就越是接近不受噪聲污染的原始信號。當奇異值數目選取過大時，降噪后的信號中仍然含有大量的噪聲。例如，奇異值數目選取為5時，與最佳的奇異值數目4相比，雖然僅僅只大1，但信號中卻出現了大量的“毛刺”，噪聲干擾很明顯。使用本文的方法，根據信號降噪后極值點數量的變化，能夠清晰地反映剩余噪聲對信號的影響，從而確定應該選取的最佳奇異值數目。

4 實驗驗證

4.1 實測頻響函數加高斯白噪聲

文獻［9］中提到，經過對分別使用頻響函數（FRF）和脈沖響應函數（IRF）構造的Hankel矩陣進行奇異值分解降噪的大量研究發現，使用FRF得到的奇異值曲線沒有明顯的拐點，不容易找到合理的閾值，在判斷奇異值分解的有效秩時，使用IRF更具優越性。但是，使用IRF對奇異值進行分解降噪，就需要把FRF先進行逆傅立葉變換，待奇異值分解降噪處理后，再通過傅立葉變換將IRF變換成FRF。

根據降噪后信號極值點數量的突變來判斷矩陣的有效奇異值數目，彌補了上述方法的不足，即利用FRF構造Hankel矩陣進行奇異值分解降噪仍能判斷出最佳的奇異值數目，避免了正、逆傅立葉變換增加的計算量。

本文通過實驗測得了頻率范圍為0～500 Hz的FRF信號，分辨率為1 Hz。由于實驗時隨機噪聲干擾不大，為了更明確地展示改進方法的有效性，對該實測信號加入了信噪比為15 dB的高斯白噪聲。加入了高噪聲污染的實測信號如圖10所示。

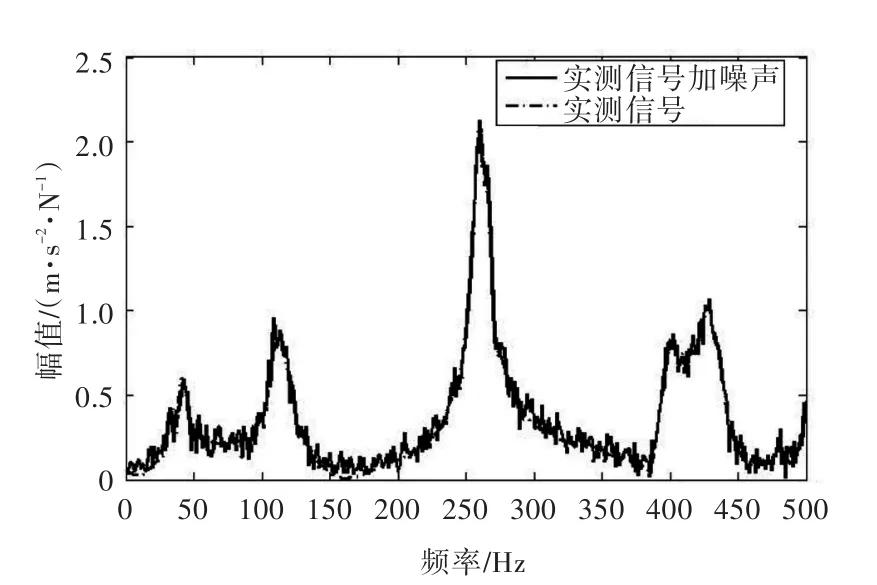
圖10 實測頻響函數信號與實測頻響函數信號加噪聲Fig.10 Measured FRF signal and measured FRF signal with additive noise

取m＝210，n＝292構造Hankel矩陣并進行奇異值分解，依照第3.2.1小節中的方法，得到奇異值序列圖如圖11所示。通過觀察圖11可發現，奇異值序列圖的拐點處呈“弧狀過渡區”，有效奇異值數目的選取不明顯，無法作出判斷。而依照第3.2.2小節中的改進方法，計算得到的極值點數量隨選取奇異值數目變化的關系如圖12所示，發現29為最優選擇。圖13所示為降噪后信號與實測信號的對比圖，其降噪后的信噪比為20.9 dB。

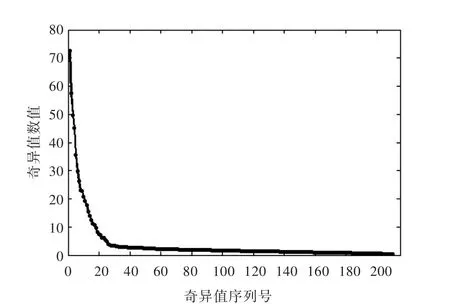
圖11 奇異值序列圖（頻響函數）Fig.11 Curve of the singular values（FRF）

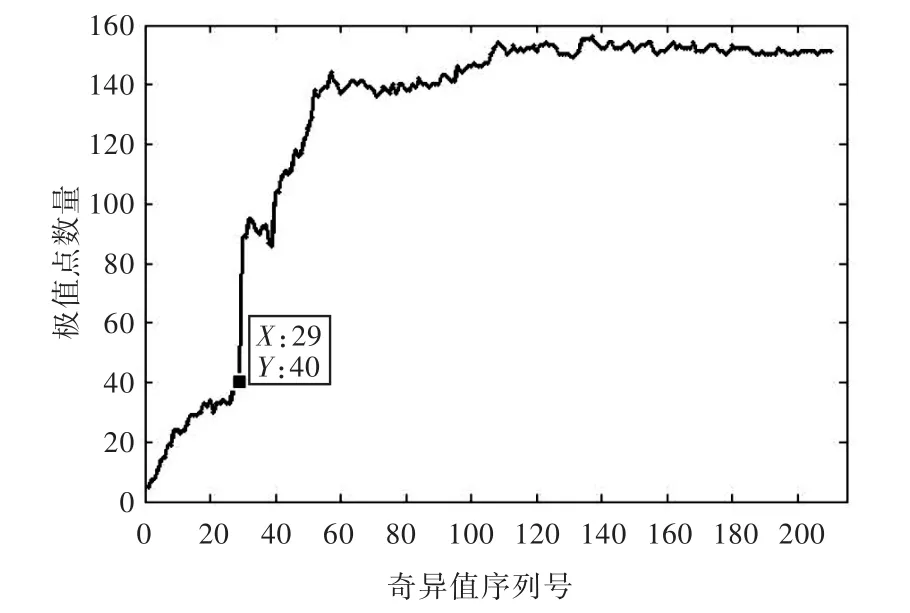
圖12 極值點數量隨奇異值數目變化的關系圖（頻響函數）Fig.12 Number of the extremum points versus the number of singular values（FRF）

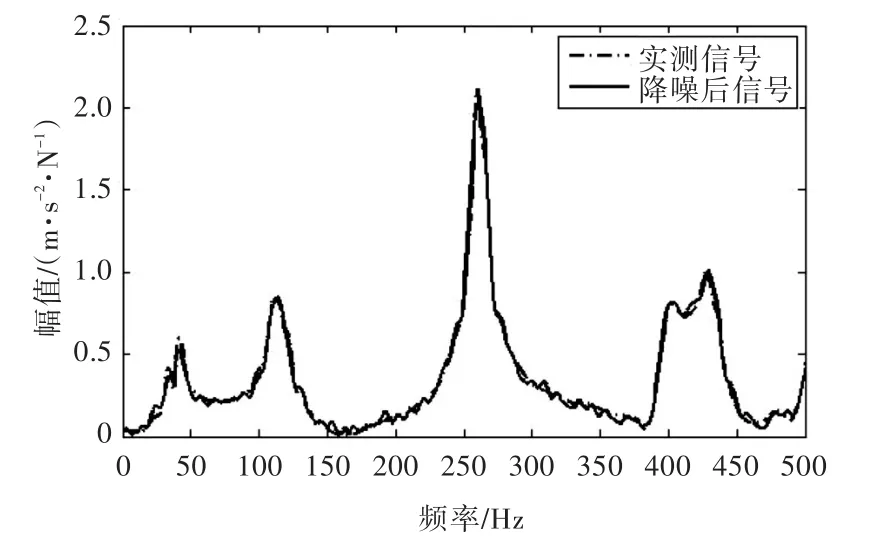
圖13 實測信號與奇異值數目為29對應的降噪信號Fig.13 Measured signal and noise elimination signal with 29 singular values

圖14所示為奇異值數目從21～38變化時信號降噪后的信噪比曲線圖。由圖可見，奇異值數目為29時，信噪比最高；當奇異值數目大于或者小于29時，信噪比都有所下降，故29為最優選擇。

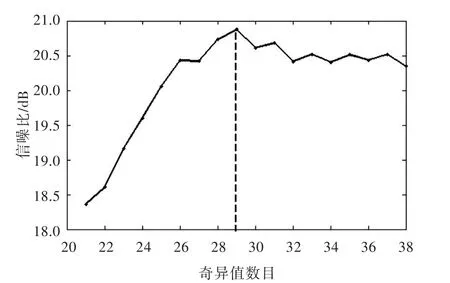
圖14 降噪信號信噪比隨選取奇異值數目變化的曲線圖（頻響函數）Fig.14 Signal to noise ratio versus the number of the singular values（FRF）

4.2 實測受噪聲干擾自功率譜

圖15為受噪聲干擾明顯的實測加速度自功率譜，頻率范圍為 0～499 Hz，分辨率為 1 Hz，同樣采用第3.2.2中的改進方法進行處理。取 m＝200，n＝301構造Hankel矩陣并進行奇異值分解，通過計算得到的降噪后信號極值點數量隨奇異值數目變化的關系如圖16所示。由圖可見，奇異值數目為11時為最優選擇，其降噪后的信號如圖17所示。

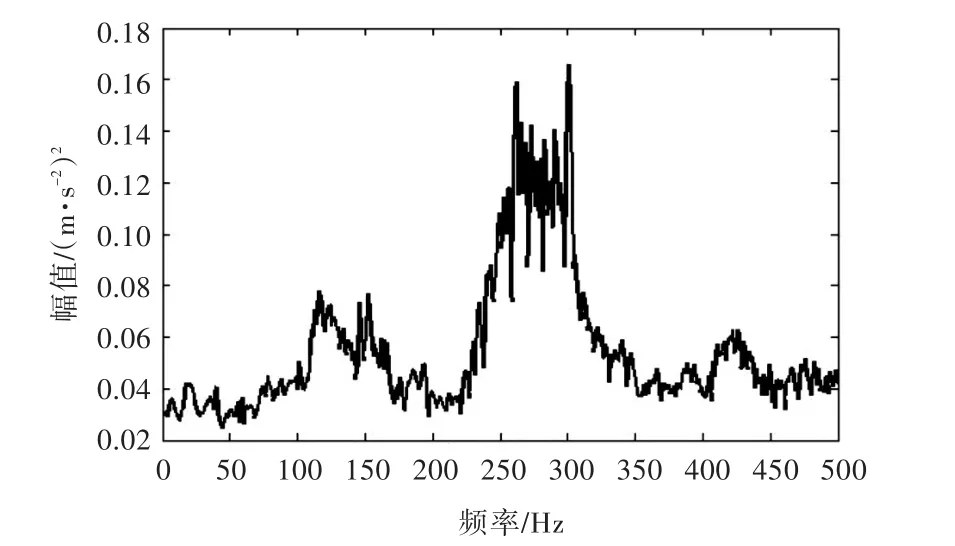
圖15 實測受噪聲干擾的自功率譜信號Fig.15 Measured noisy autospectrum signal

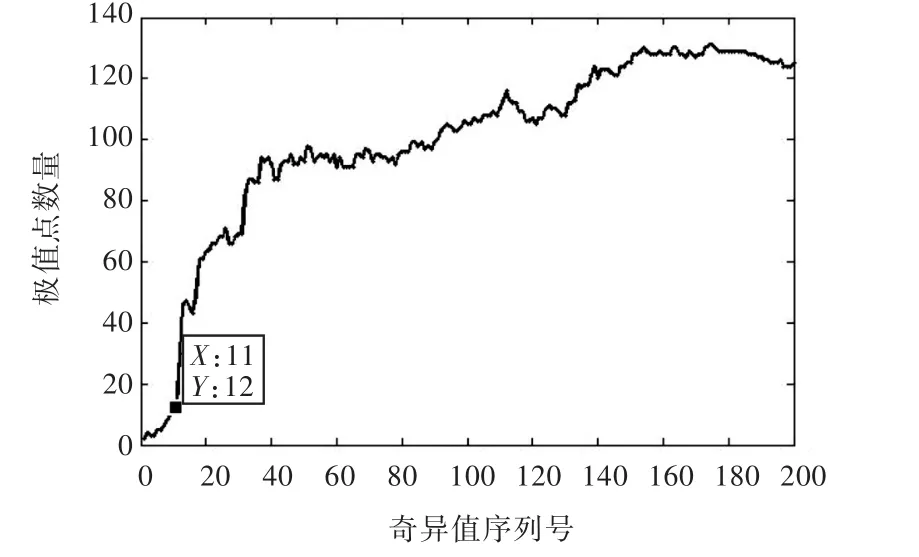
圖16 極值點數量隨奇異值數目變化的關系圖（自功率譜）Fig.16 Number of the extremum points versus the number of singular values（autospectrum）

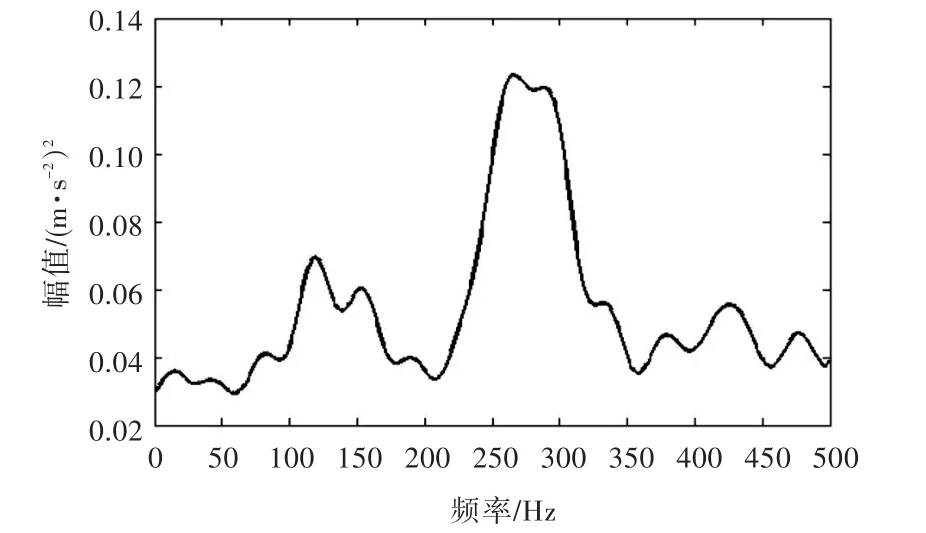
圖17 奇異值數目為11對應的自功率譜降噪信號Fig.17 Noise elimination autospectrum signal with 11 singular values

5 結 語

目前用于確定奇異值數目的方法，如奇異值曲線、奇異熵增量、信噪比經驗等，都不能明確給出有效的階次，往往只能依賴經驗進行選取。本文提出了根據降噪后信號中極值點數量的變化來確定與最優降噪結果對應的奇異值數目的方法。仿真及實驗結果表明，該方法準確、有效。在機械設備、船體結構等多種噪聲振動工程測試領域，尤其是在面臨特殊的測試環境（例如，海浪海風的影響）時，利用該方法對諸如FRF、自功率譜等測試到的信號進行降噪處理能夠得到最優的降噪效果，使測試信號具有更高的可靠性，可為正確分析后續信號提供保障。

［1］MARUDACHALAM K，WICKS A L.An attempt to quantify the errors in the experimental modal analysis［C］//The 9th International Modal Analysis Conference.Florence，1991：1522-1527.

［2］JUNG H，EWINS D J.On the use of simulated“experimental”data for evaluation of modal analysis methods［C］//Proceedings of the 10th International Modal Analysis Conference，1992：421-429.

［3］MITCHELL L D.Modal testing methods：quality，quantity and the unobtainable［J］.Sound and Vibration，1994，28（11）：10-17.

［4］FAHEY S O，WICKS A L.Noise sources in mechanical measurements［J］.Experimental Techniques ，2000，24（2）：40-43.

［5］楊文獻，姜節勝.機械］［J］.機械工程學報，2000，36（12）：9-13.YANG W X，JIANG J S.Study on the singular entropy of mechanical signal［J］.Journal of Mechanical Engineering，2000，36（12）：9-13.

［6］呂永樂，郎榮玲，梁家誠.基于信噪比經驗值的奇異值分解濾波門限確定［J］.計算機應用研究，2009，26（9）：3253-3255.LV Y L，LANG R L，LIANG J C.Decision of threshold for singular value decomposition filter based on SNR’s empirical value［J］.Application Research of Computers，2009，26（9）：3253-3255.

［7］GOLUB G H，VAN C F，LOAN V V.Matrix computations［M］.3rd Edition.Maryland：John Hopkins Studues in Mathematical Sciences，1996.

［8］修春波，劉向東，張宇河.相空間重構延遲時間與嵌入維數的選擇［J］.北京理工大學學報：自然科學版，2003，23（2）：219-224.XIU C B，LIU X D，ZHANG Y H.Selection of embedding dimension and delay time in the phase space reconstruction［J］.Journal of Beijing Institute of Technology（Natural Science Edition），2003，23（2）：219-224.

［9］SANLITURK K Y，CAKAR O.Noise elimination from measured frequency response functions［J］.Mechanical Systems and Signal Processing，2005，19（3）：615-631.