2個不等式的推廣及應用

●

(余姚市第八中學 浙江寧波 315430)

2個不等式的推廣及應用

●唐如強

(余姚市第八中學 浙江寧波 315430)

普通高中課程標準試驗教科書《數學》選修4-5“不等式選講”中有這樣2個例題：

例1如果a,b都是正數且a≠b,求證：a3+b2>a2b+ab2.

例2已知a,b為實數，求證：(a2+b2)(a4+b4)≥(a3+b3)2.

粗看起來兩者沒有內在聯系，但對例1進行等價變形：兩邊同時加上a3+b3，則有

2(a3+b3)>a3+b3+a2b+ab2,

即

2(a3+b3)>(a2+b2)(a+b)，

比較例2的結構易得到以下不等式鏈

2(a6+b6)>(a+b)(a5+b5)>(a2+b2)(a4+b4)>(a3+b3)2.

因此，猜想有以下的定理：

定理若m>0,q>0，p≥0且m>p+q,ai∈R+且i∈N+,則有

當且僅當a1=a2=…=an時取等號.

推論1若m>q>0,ai∈R+且i∈N+,則有

當且僅當a1=a2=…=an時取等號.

證明根據定理，令p=0，則

推論2若ai∈R+且i∈N+,m≥2且m∈N,則有

當且僅當a1=a2=…=an時取等號.

證明由推論1知

當ai中出現0時，可以將等于0的剔除，其他的用上面的方法可以得到證明.

例4a,b,c是正實數，且abc=1，證明：

(第37屆IMO預選試題)

證明已知a,b>0且abc=1，由定理知

同理可證

故原不等式得證.

評注(1)觀察上面的證明過程，第1個不等式中用了推論1，第2個不等式用了均值不等式，然后再考慮“1”的逆代換，目的是讓分子、分母能消去一部分.利用同樣的方法，可以推導出該不等式的一般性結果:若m,n是任意的自然數，則有

同理可證

此時n=2m+2，次數m+n=3m+2,因此，可以推得例4的一般性情況：

對于m∈N，有

(2)第26屆美國數學奧林匹克(USAMO)試題：證明對于所有正實數a,b,c，有

(a3+b3+abc)-1+(b3+c3+abc)-1+(c3+a3+abc-1)≤(abc)-1.

若令abc=1，則有

注意到

顯然該不等式是例4的加強，利用例4的推廣形式，容易得到此不等式的一般結果：

例5設a,b,c,d∈R+,ab+bc+cd+da=1,求證：

(第31屆IMO預選試題)

證明令s=a+b+c+d,則

從而

由定理可知

…

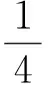
評注分析例5的證明過程，不難得到更一般性結果：

綜觀上面例題的應用可知，定理及推論不僅可以解決方冪和不等式的證明與最值問題，而且在證明過程中我們可以挖掘出規律，從而揭示出問題的實質，并能容易地將這些問題推廣到更一般性的結果.

[1] 齊行超．利用平凡不等式證明不等式舉例[J]．數學通報，2006(1)：52-53.