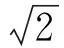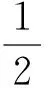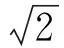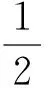活躍在中考中的動態問題分類探究

●

(錢崗中學 湖北棗陽 441221)

活躍在中考中的動態問題分類探究

●莘義成

(錢崗中學 湖北棗陽 441221)

動態問題是近年來中考中的一個熱點題型，一般是以壓軸題的方式出現.它綜合了代數(函數與方程)、空間圖形、三角形等知識，通過幾何元素(點、線、三角形、四邊形、圓)的運動變換，結合其他數學知識形成.這類題綜合性強、開放度高，解答的關鍵是要理解圖形運動前后各元素之間的數量關系，善于抓住其中不變的量和變化規律，能從運動變化的角度去思考問題，從而找到解題的突破口，還要綜合運用數形結合、分類討論、方程、函數、轉化等數學思想方法去探索解題的思路.它考查面廣，涉及的知識點眾多，留給學生很大的思維空間和思維量，需要我們在運動中分析，在變化中求解.本文以2011年全國各地中考出現的動點類問題為例進行分析，以供參考.

類型1動態問題與函數圖像結合

圖1

例1如圖1，正方形ABCD的邊長為4，P為正方形邊上一動點，運動路線是A→D→C→B→A，設點P經過的路線為x，以點A，P，D為頂點的三角形的面積是y．則下列圖像能大致反映y與x的函數關系的是

( )

A. B. C. D.

(2011年四川省宜賓市數學中考試題)

分析當點P在AD上運動時，0≤x≤4，△APD不存在，面積為0；當點P在DC上運動時，4≤x≤8，△APD隨著點P的運動面積逐漸增大，當點P到達點C時，△APD面積為8；當點P在BC上運動時，8≤x≤12，△APD隨著點P的運動面積不變仍為8；當點P在AB上運動時，12≤x≤16，△APD隨著點P的運動面積逐漸減小，當點P到達點A時，面積為0.故選B．

點評本題是一道以點運動為背景的圖像信息題，解答時必須分情況討論，從圖形和圖像上捕獲信息.本題涉及分段函數問題、幾何問題，考查觀察、分析、建模、判斷等能力，具有一定的綜合性．

類型2三角形中的動態問題

例2如圖2，在平面直角坐標系xOy中，直線AB與x軸交于點A，與y軸交于點B，且OA=3，AB=5．點P從點O出發沿OA以每秒1個單位長的速度向點A勻速運動，到達點A后立刻以原來的速度沿AO返回；點Q從點A出發沿AB以每秒1個單位長的速度向點B勻速運動．伴隨著P,Q的運動，DE保持垂直平分PQ，且交PQ于點D，交折線QB-BO-OP于點E．點P,Q同時出發，當點Q到達點B時停止運動，點P也隨之停止．設點P,Q運動的時間是t(t>0)秒．

(1)求直線AB的解析式.

(2)在點P從O向A運動的過程中，求△APQ的面積S與t之間的函數關系式(不必寫出t的取值范圍).

(3)在點E從B向O運動的過程中，完成下面問題：

①四邊形QBED能否成為直角梯形？若能，請求出t的值；若不能，請說明理由.

②當DE經過點O時，請直接寫出t的值．

(2011年福建省泉州市數學中考試題)

分析(1)在△AOB中,由勾股定理可求出點B的坐標，從而求出直線AB的解析式.

(3)當DE∥QB或PQ∥BO時，四邊形QBED都是直角梯形，用相似三角形的判定和性質，構建出一元一次方程解答即可.

(3)當DE∥QB或PQ∥BO時，四邊形QBED能成為直角梯形．

①如圖4，當DE∥QB時，因為DE⊥PQ，所以PQ⊥QB，從而四邊形QBED是直角梯形，∠AQP=90°．由△APQ∽△ABO得

故

解得

點評本題的動點在三角形的3條邊上運動，在第(1)小題中由線段的長轉化為點的坐標，進而可求出直線的解析式；第(2)小題用變量表示出三角形的面積，關鍵是用變量表示三角形的底和高；第(3)小題需在運動中的特殊時刻組成特殊的四邊形，根據點的運動情況，合理構建出對應的圖形是解答本問的關鍵.本題把函數、方程、勾股定理、直角梯形、相似三角形的判定和性質等眾多知識整合在一起，滲透了數形結合、分類討論、方程等的思想方法，具有較強的綜合性.本題可變式為“當t為何值時，△APQ是等腰三角形”.

類型3四邊形中的動態問題

(1)求點B，C的坐標；

(2)求S隨t變化的函數關系式；

(3)當t為何值時，S有最大值？求出最大值.

(2011年山東省煙臺市數學中考試題)

圖6 圖7

圖8 圖9

(2)根據點P的運動情況，應分為3種情況：當點P在AO上時，0

(3)根據第(2)小題的3種情況，分別計算出S的最大值，然后進行比較.

(2)作CM⊥AB于點M，QN⊥AB于點N，則CM=4，BM=3,從而

①如圖7，當0

③如圖9，當5

2t-8(5

點評本題中隨著點的運動，△OPQ也隨之發生變化，因此要對運動中的各類情況進行分類討論，明確點P運動過程中的關鍵點(分界點)，從而構造出不同的圖形，用變量表示出△OPQ的底和高是解答的關鍵.本題考查一次函數的圖像和性質、勾股定理、銳角三角函數、二次函數、梯形的性質等知識點，具有較強的探索性和綜合性.

類型4圓中的動態問題

圖10

例4如圖10，在平面直角坐標系中，點A(10，0)，以OA為直徑在第一象限內作半圓C，點B是該半圓周上的一動點，聯結OB，AB，并延長AB至點D，使DB=AB，過點D作x軸的垂線，分別交x軸、直線OB于點E，F，點E為垂足，聯結CF.

(1)當∠AOB=30°時，求弧AB的長.

(2)當DE=8時，求線段EF的長.

(3)在點B運動過程中，是否存在以點E，C，F為頂點的三角形與△AOB相似？若存在，請求出此時點E的坐標；若不存在，請說明理由.

(2011年浙江省金華市數學中考試題)

分析(1)易知∠ACB=60°,根據弧長公式即可求出.

(2)聯結OD，在△ODE中，由勾股定理可求出OE的長，然后利用三角形相似可求得EF的長.

(3)在點B的運動中，點E，F的位置也隨之發生變化，應分交點E在O，C之間、在點C的左側和在點C的右側3種情況，分別畫出圖形，利用相似構建出方程予以解答.

(2)如圖11，聯結OD.因為OA是⊙C直徑,所以∠OBA=90°.又因為AB=BD,所以OB是AD的垂直平分線,即OD=OA=10.

在Rt△ODE中，由勾股定理可得OE=6,從而AE=4.易證△OEF∽△DEA,可得EF=3.

圖11 圖12

圖13 圖14

(3)設OE=x.

①如圖12，當交點E在O，C之間時，由以點E，C，F為頂點的三角形與△AOB相似，有∠ECF=∠BOA或∠ECF=∠OAB.

點評本題是以動點和三角形相似結合的綜合性壓軸題，具有較強的綜合性.考查學生觀察、分析、構建圖形的能力，把動態問題變為靜態問題，從點的不同位置入手，將每種運動變化情況單獨用圖形進行表示的能力.本題涉及圓的有關性質、相似三角形、一元二次方程等知識，要注意把各種情況考慮全面，構建出每種情況的圖形是解題的關鍵.

類型5拋物線中的動態問題

例5如圖15，在平面直角坐標系xOy中，△ABC的2個頂點A，B在x軸上，頂點C在y軸的負半軸上．已知|OA|∶|OB|=1∶5，|OB|=|OC|，△ABC的面積S△ABC=15，拋物線y=ax2+bx+c(a≠0)經過點A，B，C．

圖15 圖16

(1)求此拋物線的函數表達式.

(2)如圖16，設E是y軸右側拋物線上異于點B的一個動點，過點E作x軸的平行線交拋物線于另一點F，過點F作FG垂直于x軸于點G，再過點E作EH垂直于x軸于點H，得到矩形EFGH．則在點E的運動過程中，當矩形EFGH為正方形時，求出該正方形的邊長.

(2011年四川省成都市數學中考試題)

(2)設點E的坐標為(m,m2-4m-5)，拋物線的對稱軸為x=2，根據2(m-2)=EF，列方程求解.

解得

m=1,m=-1(舍去負值).

從而

A(-1，0)，B(5，0)，C(0，-5)，

得拋物線的解析式為

y=x2-4x-5．

(2)設點E的坐標為(m,m2-4m-5)，拋物線的對稱軸為x=2，由EF=2(m-2)，得

2(m-2)=-(m2-4m-5)

或

2(m-2)=m2-4m-5，

解得

點評本題考查了二次函數的綜合運用．根據點的運動帶來圖形的變化，由正方形的性質構成一元二次方程組求解.第(3)小題探討存在性問題，此類問題是先假設存在，然后進行推理，分2種情況進行解答，根據函數與方程的轉化與應用，可組成2個不同的方程組，解出即得問題的解.本題的關鍵是采用形數結合的方法，準確地用點的坐標表示線段的長，根據圖形的特點，列方程求解，注意分類討論．

類型6幾何圖形變換中的動態問題

圖17

例6如圖17，把Rt△ABC放在直角坐標系內，其中∠CAB=90°，BC=5，點A，B的坐標分別為(1，0)，(4，0).將△ABC沿x軸向右平移，當點C落在直線y=2x-6上時，線段BC掃過的面積為

( )

(2011年湖北省黃岡市數學中考試題)

分析由點A，B的坐標,得AB=3.在Rt△ABC中，由勾股定理可求出AC=4,故點C(1，4)．當點C落在直線y=2x-6上時，y=4，x=5，從而CC′=4．根據平移的性質可得四邊形BB′C′C是平行四邊形，因此

S四邊形BB′C′C=CC′·AC=16．

點評此類問題屬于圖形的整體運動，可以說是點的運動帶動圖形的運動，求線段掃過的面積，也即運動前后所構成的圖形面積.解答時應先根據題意，構建出圖形.本題涉及到點的坐標與線段、一次函數的轉化與計算，可變式為“把運動的圖形變成特殊四邊形(如平行四邊形、矩形、菱形、正方形、梯形)、圓等圖形”.

綜上可知，解決動點問題的總體思路是：在點的運動軌跡中，尋找各種不同的情況，構造出對應的圖形，在“動”中求“靜”，在變化中求解.綜合運用數形結合、分類討論、函數、方程等數學思想和方法，從而使問題得到解決.