巧用直線參數方程解圓錐曲線中的常見問題

●

(寧波市職業技術教育中心學校 浙江寧波 315040)

巧用直線參數方程解圓錐曲線中的常見問題

●陳健

(寧波市職業技術教育中心學校 浙江寧波 315040)

已知過點P0(x0,y0)，傾斜角為θ的直線l的參數方程為

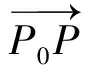
1 巧選t軸原點，解決定性問題

在用直線參數方程解題時，很多人想當然地認為P0(x0,y0)是“定點”，這樣在使用時會受到限制.其實“動”與“靜”是相對的.在實際解題過程中，可以根據是否能簡化運算來靈活選擇P0(x0,y0)作為t軸的原點，這時點P0相對于l的任意點就是“定點”.

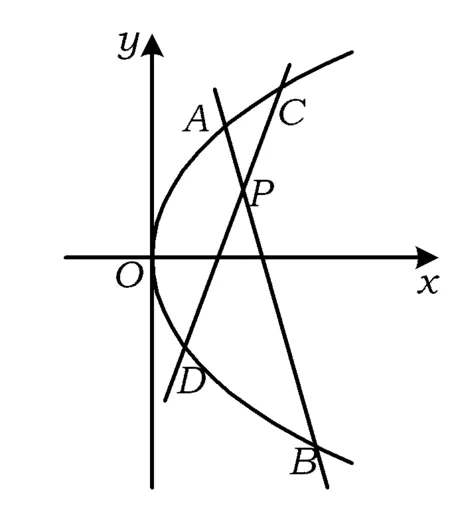
圖1

例1如圖1，點P(x0,y0)為拋物線y2=2px(p>0)內部的任意一點，過點P且傾斜角互補的2條直線與拋物線分別交于點A,B,C,D，求證:∠ACD=∠ABD．

證明設直線AB，CD的傾斜角分別為α，β，則直線AB的參數方程為

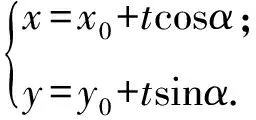
設此方程的2個根為t1,t2,則

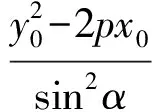
由參數t的幾何意義知

同理可得

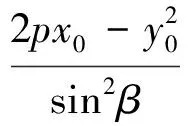
因為直線AB，CD傾斜角互補，所以

sin2α=sin2β.

由式(1)，式(2)得

AP·BP=CP·DP，

點評雖然P(x0,y0)為任意點，但是點P為動弦AB與CD所在直線的交點，由于2條弦的位置是固定的，從而點P也是相對固定的，這樣就可以選擇點P為t軸的原點，設立直線參數方程，巧妙地證明此類定性問題.若結合函數、不等式、三角函數等知識點,此方法還可以適用于解決最值問題.

2 巧用t1+t2=0，解決中點問題

圓錐曲線中有許多涉及中點和對稱性的問題，特別是存在性問題,條件比較開放，常常使學生很難入手.若用直線參數方程中參數的幾何意義來解，則能順利切入題目，解法也較為簡單.

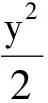
解設過點B(1，1)的直線參數方程為

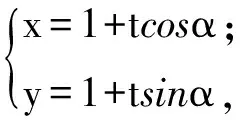
t2(2cos2α-sin2α)+2t(2cosα-sinα)-1=0.

(3)

由已知BQ1=BQ2得t1+t2=0,即

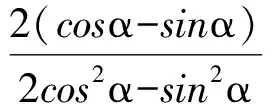
解得

sinα=2cosα，

此時式(3)簡化為

t2(2cos2α-sin2α)-1=0.

若存在這樣的直線m,使得點Q1,Q2關于點B對稱，則

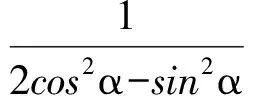
而當sinα=2cosα時，

故這樣的直線m不存在.

點評例2若按常規方法探討是否存在,消去參數后計算繁雜.現巧用t1+t2=0,使問題的解法“豁然開朗”,且運算過程較為簡潔.

3 巧用d=|t1-t2|，解決弦長問題

直線與圓錐曲線相交形成的“弦長及相關問題”是比較常見的一種題型.此類問題若用一般方法解答，則往往比較復雜且繁瑣；若能緊緊抓住直線參數方程中t的幾何意義來處理線段長度問題,則能帶來極大的方便.

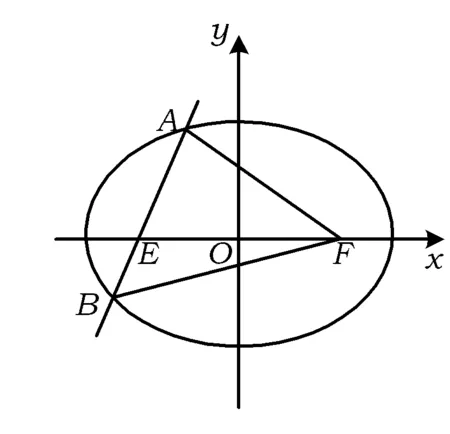
圖2

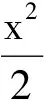
解設直線l的參數方程為

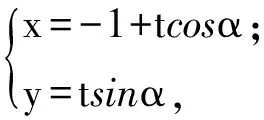
(1+sin2α)t2-2tcosα-1=0.

設點A,B所對的參數為t1,t2，其中

Δ=4cos2α+4(1+sin2α)=8>0,

且

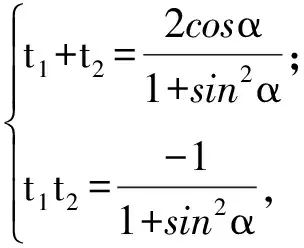
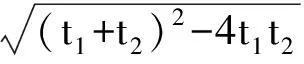
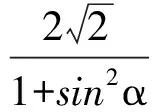
不妨設|AE| ∶|EB|=2 ∶1，則t1=-2t2，從而

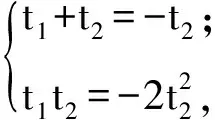
t1t2=-2(t1+t2)2，

因此

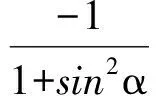
即

8cos2α=1+sin2α,

解得

從而

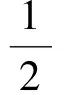
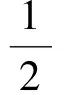
點評直線上有關線段長度的問題,在直角坐標系內一般運用距離公式

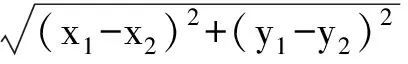
處理.在涉及多條線段且關系復雜時，利用直線的參數方程轉化為d=|t1-t2|，可將直角坐標系內的距離“一維化”，從而加快解決此類問題的速度.

4 巧用t的幾何意義，解決軌跡問題

圓錐曲線中還有一類問題是非常多見的，它就是“軌跡問題”.要用有限的條件去“捕捉”動點的“萬般”變化趨勢，特別是在“動點”個數比較多時，要建立關系式是比較困難的.下面介紹怎樣用直線參數方程中的幾何意義來處理此類問題.

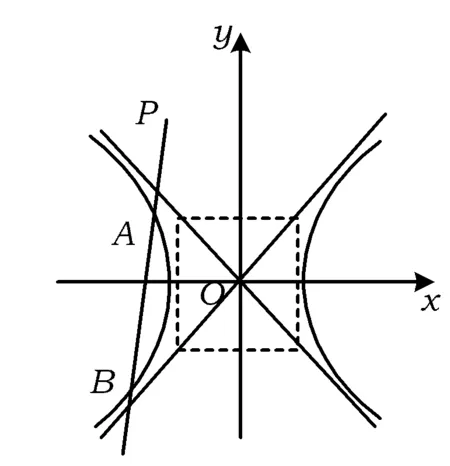
圖3

例4如圖3，已知直線y=2x+m和雙曲線x2-y2=1交于點A,B，P是這條直線上的點，且滿足條件|PA|·|PB|=5.當m變化時，求點P的軌跡方程.

解設P(x0,y0)，直線y=2x+m的參數方程為

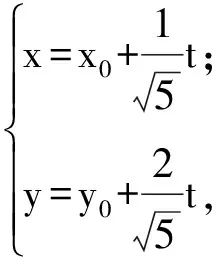
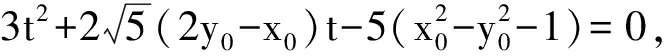
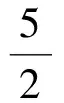
即

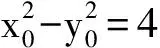
將y=2x+m代入x2-y2=1得

3x2+4mx+m2+1=0.

因為直線與雙曲線有2個不同的交點，所以

Δ=(4m)2-12(m2+1)>0，

解得

點評巧設P(x0,y0)為t軸原點，設立直線參數方程，雖然此題看似有3個“動點”比較難于解答，但利用t的幾何意義“以靜制動”，達到了出其不意的解題效果.

總之，運用直線的參數方程解圓錐曲線中的幾類題,可使有些看似復雜的問題變得簡單.同時這類解題方法思路清晰,可操作性強，學生容易掌握，并可進一步提高學生綜合運用代數、幾何三角函數知識的能力,從而激發學生的學習熱情,拓展學生思維能力.教師在教學過程中能對直線的參數方程作適當的補充與滲透,對學生數學視野的拓寬、探索能力的培養能起到較大的幫助.

[1] 彭耿玲.巧用直線的參數方程解題例說[J].福建中學數學，2009(8)：30-32.

[2] 朱斌.新課標下直線標準參數方程的應用(高三)[J].數理化學習，2009(6)：47-49.

[3] 歐陽先博.淺談直線標準式參數方程化二維為一維的解題功能[J].數學通訊，2000(10)：10-11.

[4] 高凱.直線的參數方程在圓錐曲線中的應用[J].中學教研(數學).2011(3):29-30.