基于DSP5509A的自適應系統識別的實現

傅仁壯， 李善姬

（延邊大學工學院，吉林延吉 133002）

0 引言

自適應濾波是在維納濾波等線性濾波基礎上發展起來的一種最佳濾波方法[1]。這種濾波器是根據前一時刻已知的濾波器參數，自動地調節下一時刻的參數，使得誤差信號達到最小值，最終實現最優濾波。由于自適應濾波器適合時變信號的處理[2]，因而自適應濾波技術在通信領域中應用相當廣泛。尤其是在系統識別等多個領域得到更廣泛的應用。系統識別就是應用自適應濾波器模擬一個處理過程的方法。在很多應用場合，采集數據的同時要對模型進行識別，每當提供一個新的數據，就會馬上更新模型，更新的過程就是靠自適應算法來完成的。

本文利用一個FIR濾波器作為待識別的未知系統，再應用DSPTMS320VC5509A芯片實現自適應系統識別，真正意義上達到信號處理的高精度和高效性。

1 自適應濾波器原理

自適應濾波器由濾波器和自適應算法2部分組成。其原理框圖如圖1所示。

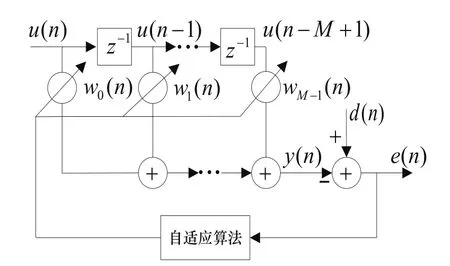
圖1 自適應濾波器原理框圖

圖1 中，u(n)為濾波器的輸入信號，y(n)為輸入信號經過數字濾波器產生的輸出信號，d(n)為濾波器的期望信號，通過d(n)與y(n)的比較可以得到濾波器的估計誤差信號e(n)。誤差信號e(n)和u(n)通過自適應算法來調節濾波器的權值系數，根據LMS或RLS等算法準則判斷e(n)是否已經達到極小值。若沒達到極小值則重復以上過程，調節濾波器的權值系數，最終使信號誤差最小，即為最佳的濾波效果。

自適應濾波器的結構一般有FIR或IIR兩種[3]，由于IIR濾波器穩定性不如FIR濾波器，因此本文中的自適應濾波器結構采用了FIR橫向濾波器結構。

其中T表示矩陣轉置運算符，時間序列為n，用M表示濾波器的階數。

2 LMS算法

傳統LMS算法是基于最小均方誤差準則(MMSE)的維納濾波器和最陡下降法提出的[4]。LMS算法基本思路是：假設已知期望信號d(n)和原始信號相關，先對FIR數字濾波器的權值設定一組任意初始值；然后根據期望信號和濾波器的輸出值之間的誤差e(n)對權值進行調 節，使下一次的誤差e(n)減少；重復上述過程，直到誤差信號最小。

假設期望信號d(n)和輸入信號u(n)是聯合各態歷經的平穩過程，我們就可以利用有限觀測樣本值的時間平均逐漸逼近統計平均，即：

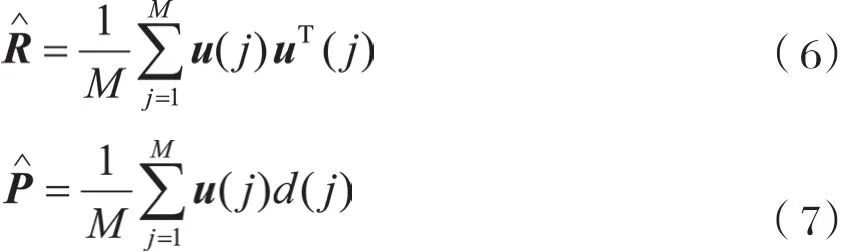
式（13）中maxλ是 自相關矩陣R的最大特征值。

3 自適應系統識別原理

自適應識別主要由自適應濾波器和未知系統構成[5]。它是通過自適應濾波器模擬一個處理過程的重要方法。如果在一個信號處理系統中，只知道系統的輸入和輸出，并不知道它的內部具體結構，可以把整個系統結構看成是一個“黑匣子”系統。自適應系統識別的主要目的就是通過對系統輸入信號和輸出信號進行分析和測試，求出系統函數或沖激響應。自適應系統識別原理框圖如圖2所示。

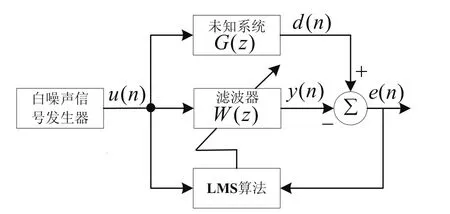
圖2 自適應系統識別原理框圖

圖2 中，G(z)是需要識別的未知系統，W(z)是FIR數字濾波器，用來模擬G(z)。白噪聲信號u(n)分別去激勵數字模型W(z)和未知系統G(z)，會得到相應的輸出信號y(n)和d(n)，通過LMS算法調整數字模型W(z)從而減小y(n)和d(n)之間的誤差。不斷的調整濾波器系數直到誤差信號達到最小，即自適應濾波器收斂。此時，濾波器的系數就能完整地把未知系統描述出來。

4 自適應系統識別的DSP實現

為了提高自適應系統識別的處理速度和精確度，采用TI 公司的TMS320VC5509A芯片實現，該處理器采用程序與數據分開的哈佛體系結構[6-8]，具有高度的并行性。

在實際工程應用中需要識別的系統都是未知的，為了覆蓋未知系統的所有零點和極點，輸入信號u(n)的頻譜應該寬廣，一般情況采用線性調頻脈沖信號或者是白噪聲信號。在本次實驗中，采用rand( )函數構建一個零均值隨機噪聲發生器，用來產生自適應濾波器和未知系統所需要的測試數據。rand( )函數能產生一個0到32 767的16位有符號整數，再把得到的數值減去0x4000就可以得到一個從-16384到16383數值的零均值偽隨機序列。具體的C語言程序代碼如下：

# include ＜math．h＞

# define unsigned int uint

# pragma CODE_SECTION (rhs,”sj_dm”);

void rhs (int *x , uint S)

{

uint i;

for (i =S; i＞0;i++)

*x++ =rand( ) -0x4000;

}

自適應系統識別的程序流程圖，如圖3所示。

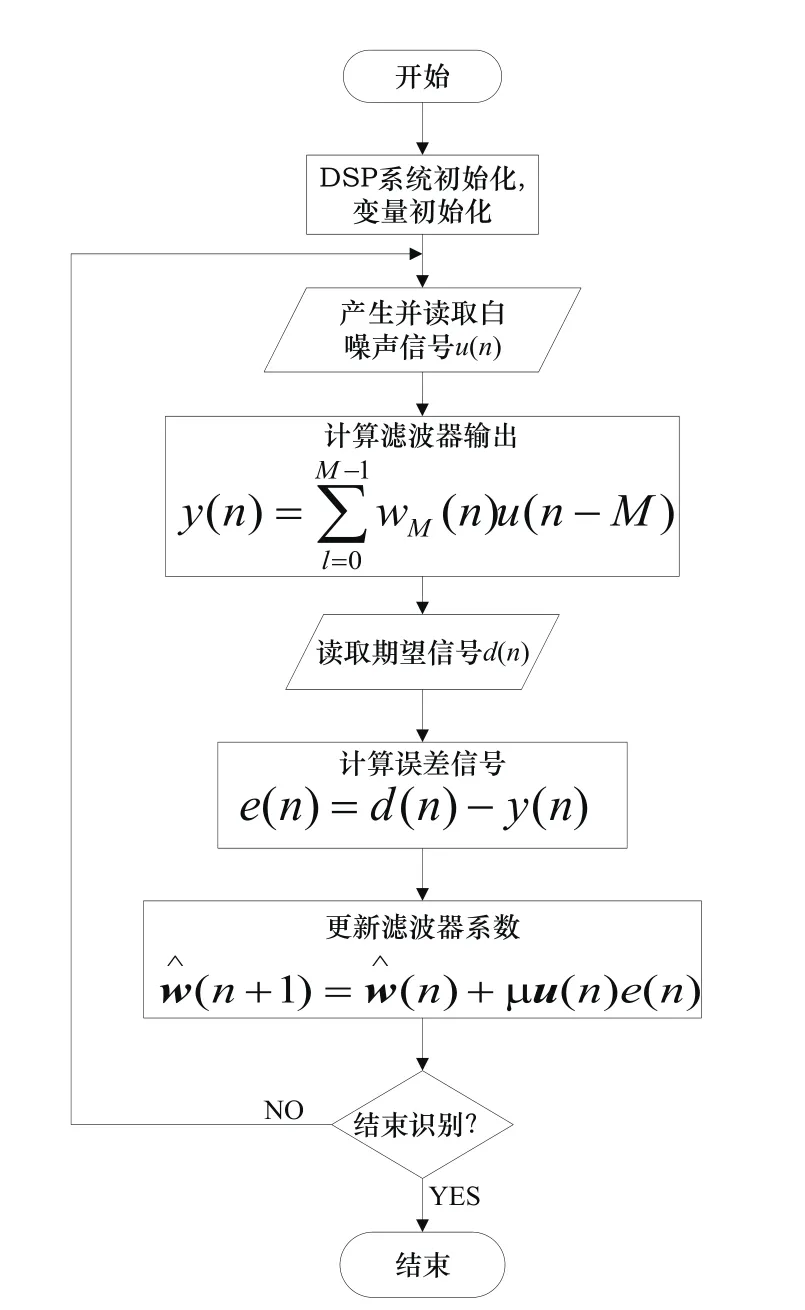
圖3 自適應系統識別程序流程圖

采用C語言編程后，把調試好的程序下載到TMS320VC5509A片內存儲器，再在view菜單選項下設置相應的參數，用來顯示未知系統和識別系統的波形以及頻譜。通過對以下4圖對比可以知道，自適應LMS算法收斂以后，自適應系統識別模型和未知系統的頻域響應和沖激響應高度一致，未知系統的特征可以由自適應系統識別模型精確地描述出來，真正意義上實現了自適應系統對未知系統的高精度識別。

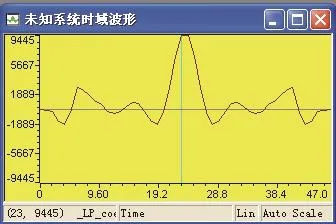
圖4 未知系統傳遞函數時域波形

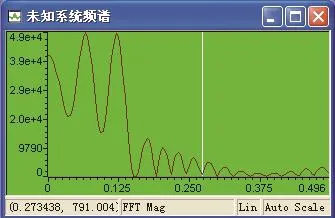
圖5 未知系統傳遞函數頻譜

圖6 自適應系統識別未知系統的時域波形

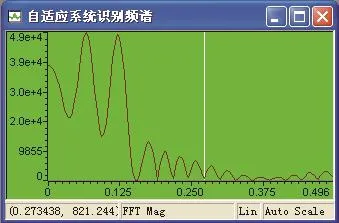
圖7 自適應系統識別未知系統的頻譜

5 結束語

在信號處理領域，自適應系統識別的方法是非常重要的。本文在論述LMS算法的自適應濾波器原理和自適應系統識別原理的基礎上，采用rand( )函數構造一個隨機白噪聲信號發生器, 使輸入信號u(n)具有寬廣頻譜，從而覆蓋未知系統的所有零點和極點，并且用來產生自適應濾波器和未知系統所需要的測試數據。最后利用TI公司的DSP TMS320VC5509A芯片實現了自適應系統識別。通過實驗可以得出，利用該方法對未知系統的識別可以真正意義上達到信號處理的高精度和高效性。

[1] 張婷瑞,李善姬,丁景龍．基于LabVIEW和MATLAB混合編程的自適應濾波器設計[J]．電子測試, 2009(1):40-43．

[2] 余榮．自適應濾波器在噪聲消除中的應用與研究[D]．南昌:南昌航空大學,2008:4-38．

[3] 王麗芳,陳益平．基于DSP的自適應濾波器的實現[J]．計算機仿真,2009,26(9):281-284．

[4] 王秀芳,劉凱,馬賽．基于改進LMS算法的自適應濾波器[J]．大慶石油學院學報,2009,33(6):94-97．

[5] 吳宵,葉水生,黃珍．基于自適應濾波器的系統識別研究 與實現[J]．微計算機信息,2007,23(2-1):275-277．

[6] 馮炳樞,羅飛,許玉各,等．基于LMS 算法自適應濾波器信息采集系統設計[J]．計算機工程,2009,35(3):266-272．

[7] Song W C,Lin F．DSP-based communication for monitoring and control in variable frequency drives [J]．Power Systems and Communications for the future,2005(9):61-64．

[8] 陳書林,柳媛慧．P2P網絡中基于節點能力自適應的搜索算法[J]．湖南科技大學學報:自然科學版,2009,24(2):61-65．