基于MATLAB對二維混合邊界靜電場域的分析

李小兵

（蘭州交通大學，電子與信息工程學院， 甘肅蘭州 730070）

0 引言

當電磁波通過兩個不同的媒質邊界時，邊界附近的電磁場需要滿足一定的規則，即邊界條件，它把場量、介質的材料特性及邊界面上的電荷及電流密度聯系在一起，邊界條件可以從基本的電磁定律得到。由于描述電磁場的偏微分方程是空間坐標的函數，因此只有在一組特定的邊界條件下才能獲得唯一解。分離變量法和鏡像法都是求解靜態場邊值問題解析解(精確解)的方法，但它們只有對一些特殊對稱的邊界才是可行的。在許多實際問題中,往往由于邊界條件過于復雜而無法求得解析解,這時一般要借助數值法求二維靜態場域的電位所求得的。而應用有限差分法在對靜電場進行求解的結果比較誤差較小，不僅數學建模和編程有規可循，而且場域內的電位分布情況還可以用圖示一目了然,便于分析。大部分電磁場問題涉及3種類型的邊界條件：狄里赫利（Dirichlet）型邊界條件、紐曼（Neumann）型邊界條件、混合型邊界條件，有限差分法對二維混合邊界靜電場域中的電位進行計算時涉及到了第一和第二類邊界條件。

1 理論分析

1.1 二維場域的邊界條件

如圖1所示，區域S的邊界為曲線L所包圍，若二維場域邊界上的電位φ=f,f是一個事先已知的點位函數，這種邊界條件為第一類邊界條件（狄里赫利邊界條件）。若二維場邊界滿足為已知數或一種連續函數(見圖2），這種邊界條件為第二類邊界條件（紐曼邊界條件），若二維場邊界條件為第一第二種線性組合（見圖3），則稱為混合邊界條件。

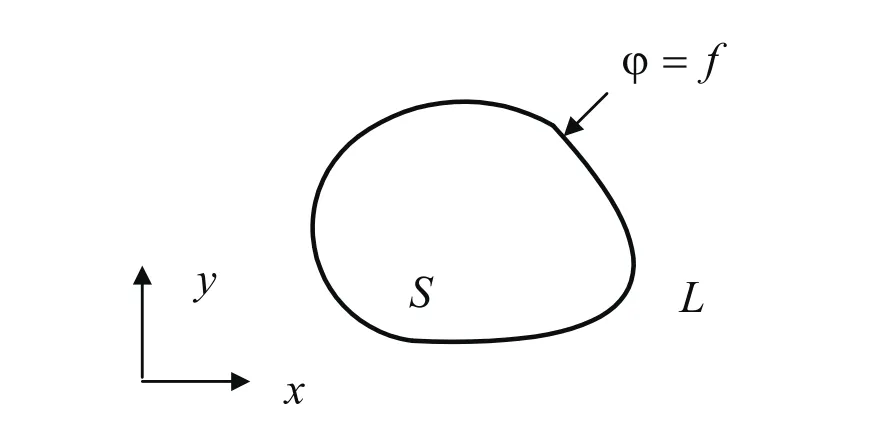
圖1 狄里赫利型邊界條件

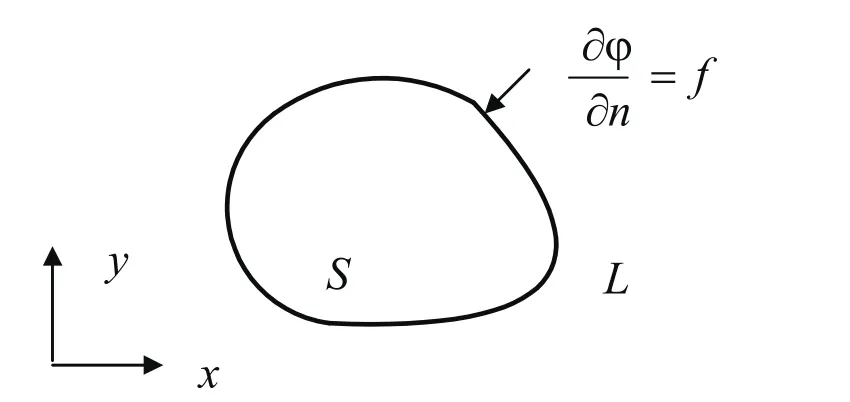
圖2 紐曼型邊界條件

圖3 混合型邊界條件

1.2 對邊界條件的處理

對第一類邊界條件φ|L=f，若場域的網格節點都落在邊界L上，無需處理，若不重合，一種是所謂的直接轉移法汲取最靠近0點邊界函數值做0點，這種方法比較粗糙誤差大。一種是線性插值，先判斷X方向的和Y方向上哪個節點更靠近節點0，如1靠近，可得X方向線性插值0的值（見圖4）。

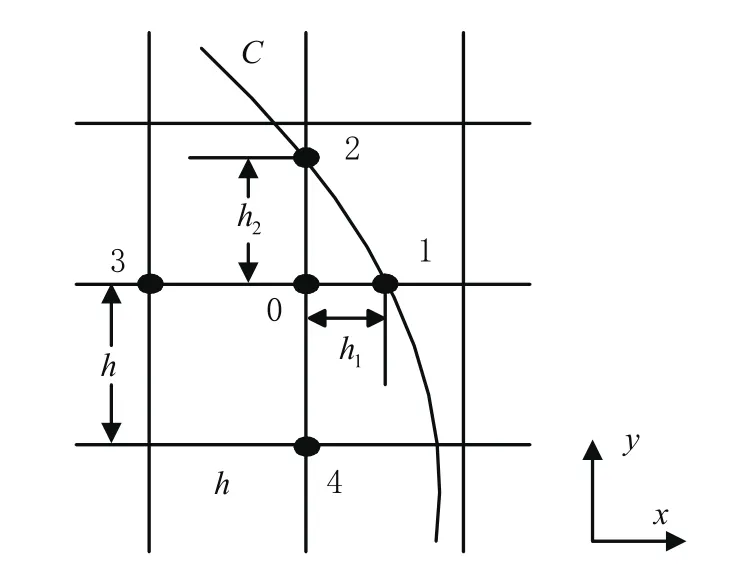
圖4 第一類邊界條件差分格式

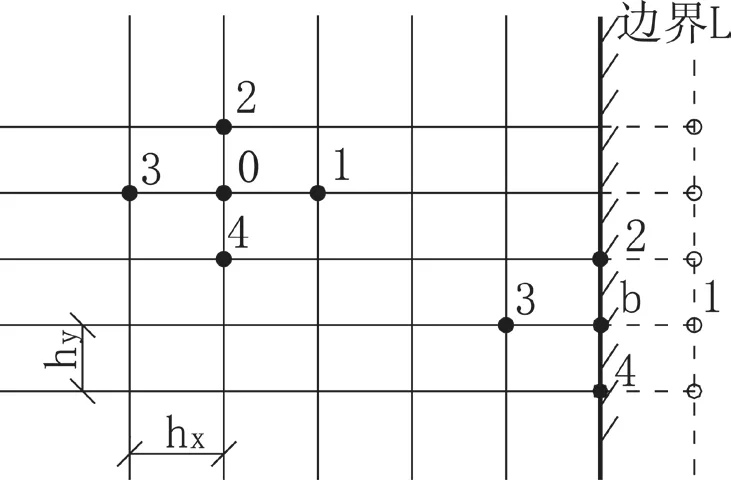
圖5 網格線與邊界重合

2 超松弛法

簡單迭代在解決實際問題中收斂速度慢，占用存儲單元多（需兩套存儲單元分別存放全部節點使用價值不大，采用超松弛發可以很好的解決。

將剛才算出的左下角的點（i-1，j）和點（i，j-1）代替上次計算的點（i-1，j）和點（i，j-1），即：

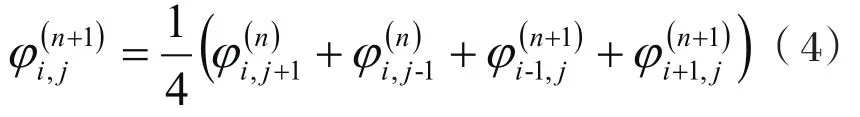
上式稱為高斯-賽德爾迭代法，引入一個松弛因子ω上式改為

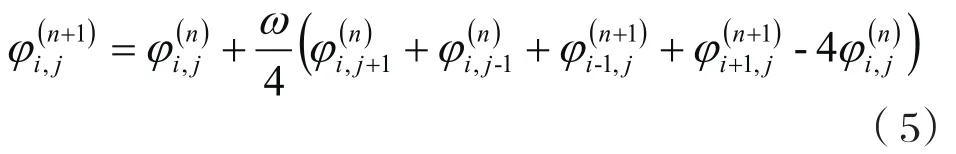
式中，松弛因子ω最佳值為：

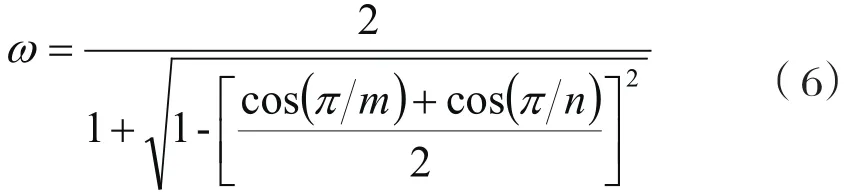
3 計算結果和討論

一個長直接地金屬槽，側壁和底面電位為零，頂蓋為?= 1 00sinπx，計算槽內電位分布：

槽中電位函數?滿足拉普拉斯方程：

其邊界條件滿足混合邊界條件：

MATLAB計算程序框圖如圖6所示。

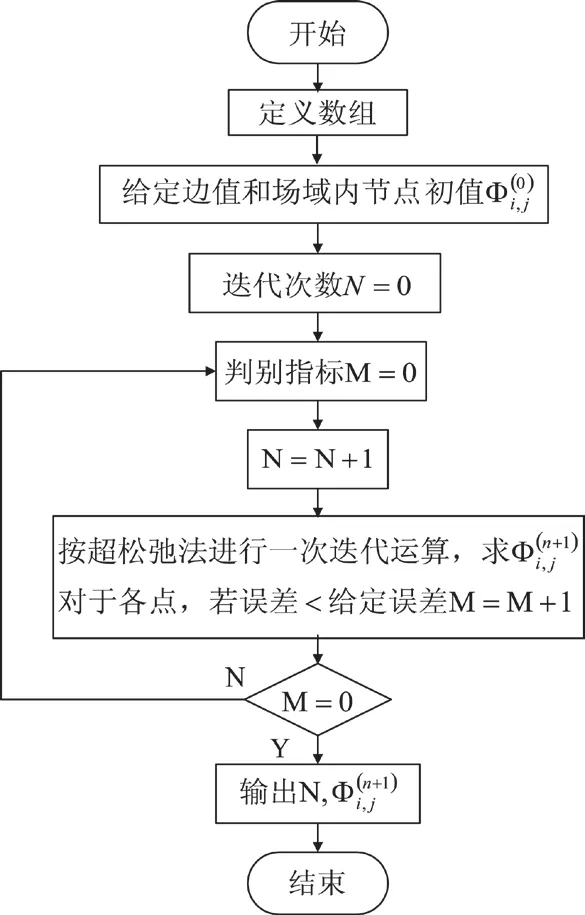
圖6 計算程序框圖

通過MATLAB編程，程序運行結果是：迭代次數k=111，收斂因子w=1.6093，即經過節點111次的迭代后，電位值收斂于一固定值，且誤差小于10-8，場域內各網格節點電位計算結果如表1所示。

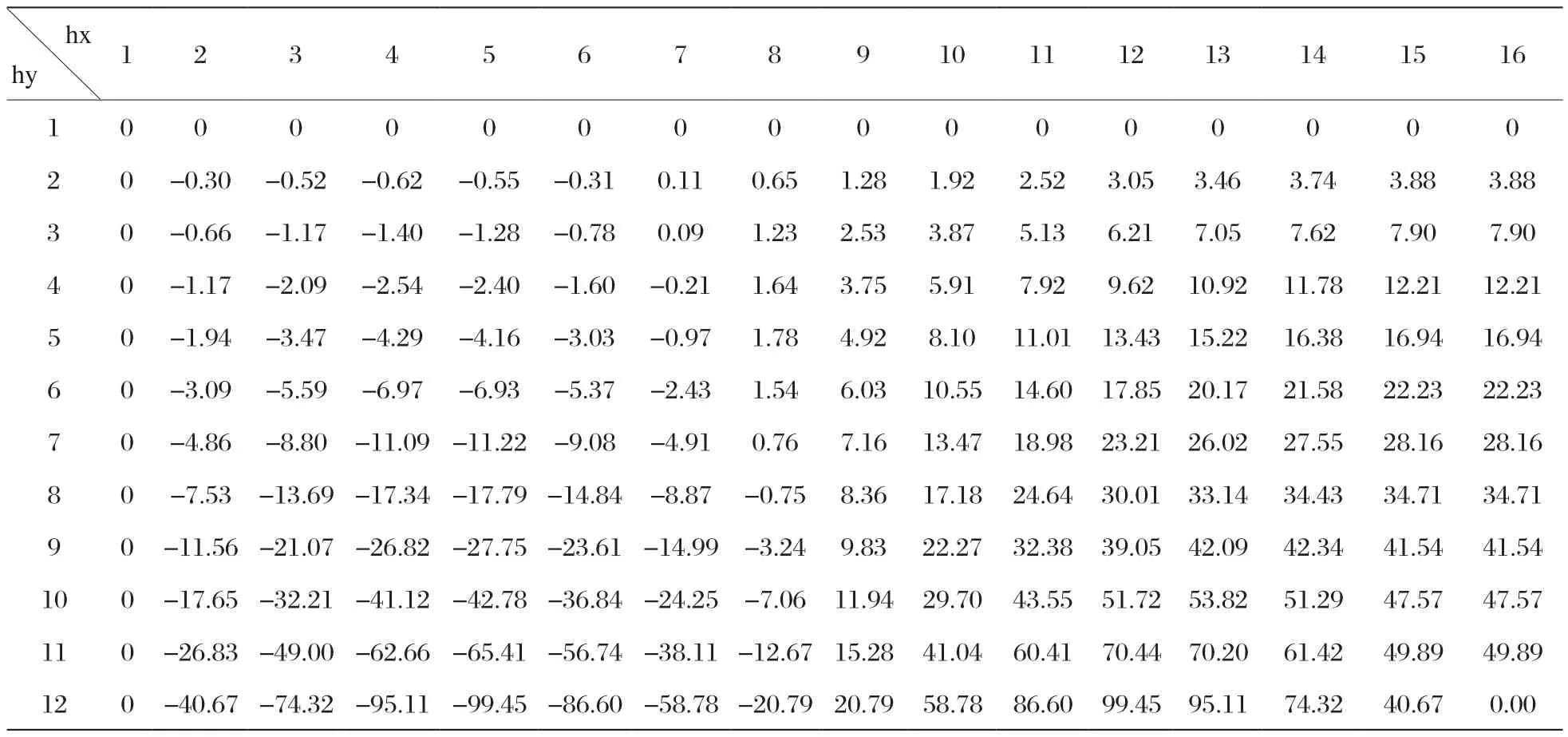
表1 域內網格點電位的計算結果（hx=16,hy=12,誤差小于10-8）

應用MATLAB繪制二維混合邊界靜電場區域內電位分布三維曲面圖、域內等位線及電場線分布如圖7所示。

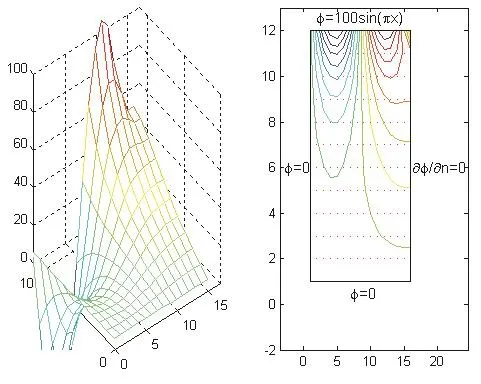
圖7 二維混合邊界靜電場電位分布圖

我們在應用簡單迭代法進行處理，同樣要求誤差小于10-8，通過MATLAB編程行結果是：迭代次數k=410，即經過節點410次的迭代后，電位值收斂于一固定值，且誤差小于10-8，場域內各網格節點電位計算結果與超松弛法相同。

4 結論

1）混合邊界條件屬于復雜邊界問題，很難求出解析解，但工程中常常要分析其中的電位分布，借助數值法求解才能進行，本文采用有限差分法很好地解決了靜態場混合邊界條件下的電場分布問題。應用MATLAB編程求解差分方程，由于混合邊界條件比單一邊界條件情況復雜得多，給編程帶來麻煩，但比解析法工作量要小。

2）通過兩種有限差分求解方法，應用超松弛法只需計算好合適的松弛因子就可以大大加快收斂速度，應用超松弛法迭代次數k=111,而得到同樣的結果簡單迭代法需要410次，因此應用超松弛法，即節省時間還節省計算機的存儲空間。

利用MATLAB 強大的計算與圖像處理功能分析研究電磁場與電磁波問題簡單方便，特別對于抽象不可見的問題進行仿真處理，可直觀地分析和理解問題。文中對靜電場二維場混合邊界條件進行處理并建立相應的數學建模，通過 MATLAB編程計算和繪圖能力，準確地描繪出等勢線分布和空間電場強度分布圖。

[1] 王秉中.計算電磁學[M].北京:科學出版社, 2002:19-51.

[2] Mai Lu,Paul J.Leonard.Dependence of ridge positionon the cutoff wave-length of the dominant mode in sin-gle ridge waveguides[J].Microwave and Optical Tech-nology Letters,2002,34:374-377.

[3] Pyle J R.The cutoff wavelength of the TE10 mode inridged rectangular waveguide of any aspect ratio[J].IEEE Trans Microwave Theory Tech,1966 ( MTT-14):175-183.

[4] 洪偉.計算電磁學研究進展[J].東南大學學報:自然科學版,2002(5):336-338.

[5] 孫海,褚衍東.非對稱單脊波導主模截止波長的數值計算[J].蘭州交通大學學報,2006(3): 84-88.

[6] Rong Y,Zaki K A.Characteristics of generalized rec-tangular and circular ridge waveguides[J].IEEE TransMicrowave Theory Tech,2000( MTT-48):258-265.

[7] 何紅雨.電磁場數值計算法與MATLAB實現[M].武漢:華中科技大學出版社,2002.

[8] 樓順天,于衛,閆華梁.MATLAB程序設計語言[M].西安:西安電子科技大學出版社,1998.