基于強度條件的黃土結構性靜力試驗研究

田堪良，張慧莉，馬 俊

（1.西北農林科技大學 水土保持研究所，陜西 楊凌 712100；2.中國科學院水利部 水土保持研究所，陜西 楊凌 712100；3.西北農林科技大學 水利與建筑工程學院，陜西 楊凌 712100；4.中國石油天然氣股份有限公司西氣東輸管道分公司，上海 200122）

1 引 言

土體的結構是其強度、變形的內在決定因素。土的結構性對其工程性質的重要性已成為共識，沈珠江[1]認為，土結構性的研究是“21世紀土力學的核心問題”。黃土是一種典型的結構性土，其獨特的結構性是其發生脆性破壞、濕陷的重要原因。為了探究黃土結構性對其力學特性的影響，許多學者也做了大量工作，高國瑞[2－4]研究指出，黃土中存在架空大孔隙是黃土具有濕陷性的內在原因。苗天德[5]、王蘭民[6]和陳正漢[7]等采用電子顯微鏡、數字掃描電境和CT成像技術對黃土的微觀結構變化和力學宏觀表現進行了研究。近年來，許多研究者采用土力學的方法研究黃土的結構性，取得了豐碩的成果。謝定義等[8－10]研究者先后提出了反映黃土結構性的定量化參數，并將其引入土的變形本構關系和強度本構關系，使結構性土的研究具有了新的特色。邵生俊等[11－12]通過三軸試驗，由原狀土、重塑土和飽和土的主應力差比值提出了另一種結構性參數，并將結構性參數引入到原狀黃土應力-應變關系分析中，建立了非飽和濕陷性黃土的本構模型。陳存禮等[13]根據同壓力下原狀、重塑及飽和黃土的孔隙比定義了一個結構性定量參數，并通過試驗研究了原狀黃土的結構性隨壓力及含水率變化的規律性。駱亞生等[14－15]基于三軸試驗提出了反映黃土結構性的應變綜合結構勢參數，建立了對應于復雜應力條件的土結構性本構模型。

筆者在文獻[16]中提出黃土顆粒之間的力由兩種力組成，一種是聯結力，屬于短程力，包括土顆粒之間化學膠結力、分子引力以及吸力，這些力形成了黃土的聯結結構強度；另一種力是摩擦力，屬于遠程力，是土體受力時土顆粒之間的聯結力被克服后有相互錯動、移位、重新排列的運動或趨勢時才產生的阻止土體變形的力，包括顆粒之間的摩擦力、咬合力，這種力形成了黃土的摩擦結構強度，黃土的結構強度就是由聯結結構強度和摩擦結構強度組成的。并提出了黃土聯結結構強度、摩擦結構強度、壓密強度以及壓密變形的定量化概念。本文將在此基礎上從強度的角度定量分析黃土的結構性，提出定量描述黃土結構性的基于強度條件的黃土靜力結構性參數，通過三軸試驗研究黃土的結構性及其變化規律。

2 基于強度條件的黃土靜力結構性參數

黃土的結構性強弱可以通過結構破壞、弱化后強度變化的大小反映出來，因此，可通過原狀黃土、重塑黃土及飽和重塑黃土靜三軸試驗得出的強度差異來分析原狀黃土的結構性。

圖1為原狀黃土、重塑黃土和飽和重塑黃土靜三軸試驗應力-應變曲線，qo、qr及qs分別為某一應變ε時原狀黃土、重塑黃土和飽和重塑黃土的強度值（σ1-σ3）。相同應變ε時，原狀黃土的強度值qo最大，飽和重塑黃土的強度值qs最小。（qoqr）的大小反映了原狀黃土的聯結結構的強弱，以mε1=(qo-qr)/qs來反映原狀黃土聯結結構的強弱，稱之為黃土的聯結結構靜力強度勢參數。m1ε越大，表明原狀黃土的聯結結構性愈強，聯結結構被完全擾動破壞后的強度損失越大，因此，m1ε反映了黃土聯結結構所蘊藏的結構強度勢。

(qr-qs)的大小反映了重塑黃土遇水后結構的弱化和結構強度的損失。可以 mε2=(qr-qs)/qs來表示重塑黃土摩擦結構性的強弱，稱之為黃土的摩擦結構靜力強度勢參數。mε2越大，表明重塑黃土的摩擦結構性愈強，摩擦結構遇水弱化后強度損失越大，因此，mε2反映了黃土摩擦結構所蘊藏的靜力強度勢。

黃土所蘊藏的聯結結構勢和摩擦結構勢之和即為黃土所蘊藏的總的結構勢，可以用黃土的聯結結構靜力強度勢和摩擦結構靜力強度勢之和即mε=mε1+mε2來反映黃土所蘊藏的總的結構強度勢，稱之為黃土的結構靜力強度勢參數。mε既包含了黃土的聯結結構靜力強度勢，又包含了黃土的摩擦結構靜力強度勢，綜合反映了黃土結構性的強弱，可作為一個定量描述黃土結構性的參數。

圖1 原狀黃土、重塑黃土和飽和重塑三軸試驗應力-應變曲線Fig.1 Stress-strain curves of intact loess,remolded loess and saturated remolded loess

3 試驗土樣與試驗方法

試驗所用黃土土樣均取自陜西楊凌的渭河Ⅱ級階地，取土深度為3.5～4.0 m，屬于Q3黃土。試驗土樣的物理性質指標見表1。

試樣分為原狀試樣、重塑試樣和水泥結構性試樣，重塑試樣和水泥結構性試樣分為3種干密度：1.26、1.4、1.5 g/cm3，采用分層壓樣法制備，對應的飽和含水率分別為42.5%、34.5%、29.8%，用水膜轉移法或風干法按要求調節試樣的含水率，飽和樣采用抽氣飽和的方法進行飽和。

試驗采用固結不排水（測孔隙壓力CU），剪切速率為每分鐘應變為0.3%。

4 基于強度條件的黃土結構性分析

4.1 黃土聯結結構靜力強度勢分析

圖2所示分別為不同含水率ω的原狀黃土和水泥人工結構性黃土的聯結結構靜力強度勢參數曲線。從圖中可以看出：①隨著應變的增大，原狀黃土和水泥人工結構性黃土的聯結結構靜力強度勢參數在小應變（ε1＜3%）時快速減小，應變較大時減小速度放緩，最后趨于平穩，表明聯結結構在受力初期損傷破壞比較快、比較大，也表明原狀黃土和水泥人工結構性黃土的結構損傷破壞主要發生在小應變階段即應變ε1＜3%的階段，三軸應力條件下在較小的荷載作用下黃土的聯結結構就很容易被損傷破壞；②在同一含水率下不同圍壓的聯結結構靜力強度勢參數曲線均處在一較窄的條帶范圍內即聯結結構靜力強度勢參數數值比較接近，表明聯結結構靜力強度勢參數受圍壓的影響較小，本文所提出的聯結結構靜力強度勢參數對不同圍壓有較好的歸一性。

圖3所示為原狀黃土與人工結構性黃土聯結結構靜力強度勢參數平均值（4個圍壓的平均值）曲線。由圖可以看出：含水率為ω=17.8%的不同密度和水泥含量的人工結構性黃土的聯結結構靜力強度勢參數曲線與含水率為ω=17.8%及ω=26%的原狀黃土的聯結結構靜力強度勢參數曲線具有相似的形態，而且人工結構性黃土的聯結結構靜力強度勢參數曲線基本上均處在這兩條原狀黃土聯結結構靜力強度勢參數曲線之間，這表明采用水泥作為膠結材料模擬原狀黃土的聯結結構強度是可行的。

表2為不同狀態下黃土的聯結結構靜力強度勢參數mε1的最大值（4個圍壓的平均值曲線的最大值）。可以看出，不同含水率時原狀土的聯結結構靜力強度勢參數存在明顯差異，含水率越小，聯結結構靜力強度勢參數越大，表明，含水率是影響黃土聯結結構靜力強度的主要因素，含水率越小，聯結結構性越強；相同含水率條件下，干密度為ρd=1.26 g/cm3時，人工結構性黃土的聯結結構靜力強度勢參數mε1隨水泥含量的增加而增大，表明，水泥含量越高，土顆粒之間的膠結力越強，黃土的聯結結構性越強。

Fig.2 黃土聯結結構靜力強度勢參數曲線(ρd= 1.26 g/cm3)Fig.2 Curves of link structural static strength potential parameter for loess (ρd= 1.26 g/cm3)

圖3 原狀黃土與人工結構性黃土聯結結構靜力強度勢參數(平均值)曲線Fig.3 Curves of link structural static strength potential parameter (averages) for intact loess and artificial structural loess

表2 黃土聯結結構靜力強度勢參數mε1的最大值Table2 Maximum values of mε1

4.2 黃土摩擦結構靜力強度勢分析

圖4所示分別為不同含水率的原狀黃土的摩擦結構靜力強度勢參數曲線。從圖中可以看出：① 當含水率很小（ω=5%）時，隨著應變的增大，黃土的摩擦結構靜力強度勢參數在小應變（1ε＜1%）時快速增加，達到峰值后，隨著應變的增大又快速減小，當應變1ε＞5%后減小速度放緩、最后趨于平穩。這是由含水率很小時，黃土顆粒之間的摩擦力很大，摩擦強度也很大，在較小的力作用下結構難以被破壞，隨著軸力的增大，結構才逐漸損傷破壞，摩擦結構強度才逐漸發揮出來，摩擦結構靜力強度勢參數mε2也逐漸達到最大。隨后，摩擦結構的不斷損傷破壞，摩擦結構靜力強度勢參數mε2開始減小，并趨于平穩。②當含水率較大（ω=17.8%）時，摩擦結構靜力強度勢參數隨著應變的增加由小應變時的逐漸減小到趨于平穩，再到后來略有增大。這表明當含水率較大時，黃土的摩擦結構強度較小，在小應變（軸向力較小）時，摩擦結構損傷破壞快速較大，摩擦結構靜力強度勢參數隨著應變的增加減小較快，隨著顆粒的相互錯動、重新排列，形成了新的相對更加穩定的摩擦結構，摩擦結構的損傷破壞速度放緩，摩擦結構靜力強度勢參數趨于平穩，但隨著應變的增大，軸向力也不斷增大，新的摩擦結構又被逐漸損傷破壞，破壞速度也略有增加，所以，摩擦結構靜力強度勢參數又隨應變的增大逐漸略有增大。③同一含水率下不同圍壓的摩擦結構靜力強度勢參數曲線同樣均處在一較窄的條帶范圍內即摩擦結構靜力強度勢參數數值比較接近，表明摩擦結構靜力強度勢參數受圍壓的影響較小，本文所提出的摩擦結構靜力強度勢參數對不同圍壓有較好的歸一性。

圖5為不同含水率的重塑黃土的摩擦結構靜力強度勢參數平均值（4個圍壓的平均值）曲線。可以看出：不同含水率時重塑黃土的摩擦結構靜力強度勢參數存在明顯差異，含水率越小，摩擦結構靜力強度勢參數越大；摩擦結構靜力強度勢參數在小應變時差值較大，隨著應變的增加差值減小，且趨于平穩。這表明，含水率同樣也是影響黃土摩擦結構強度的主要因素，含水率越小，摩擦結構強度越大，摩擦結構性越強。

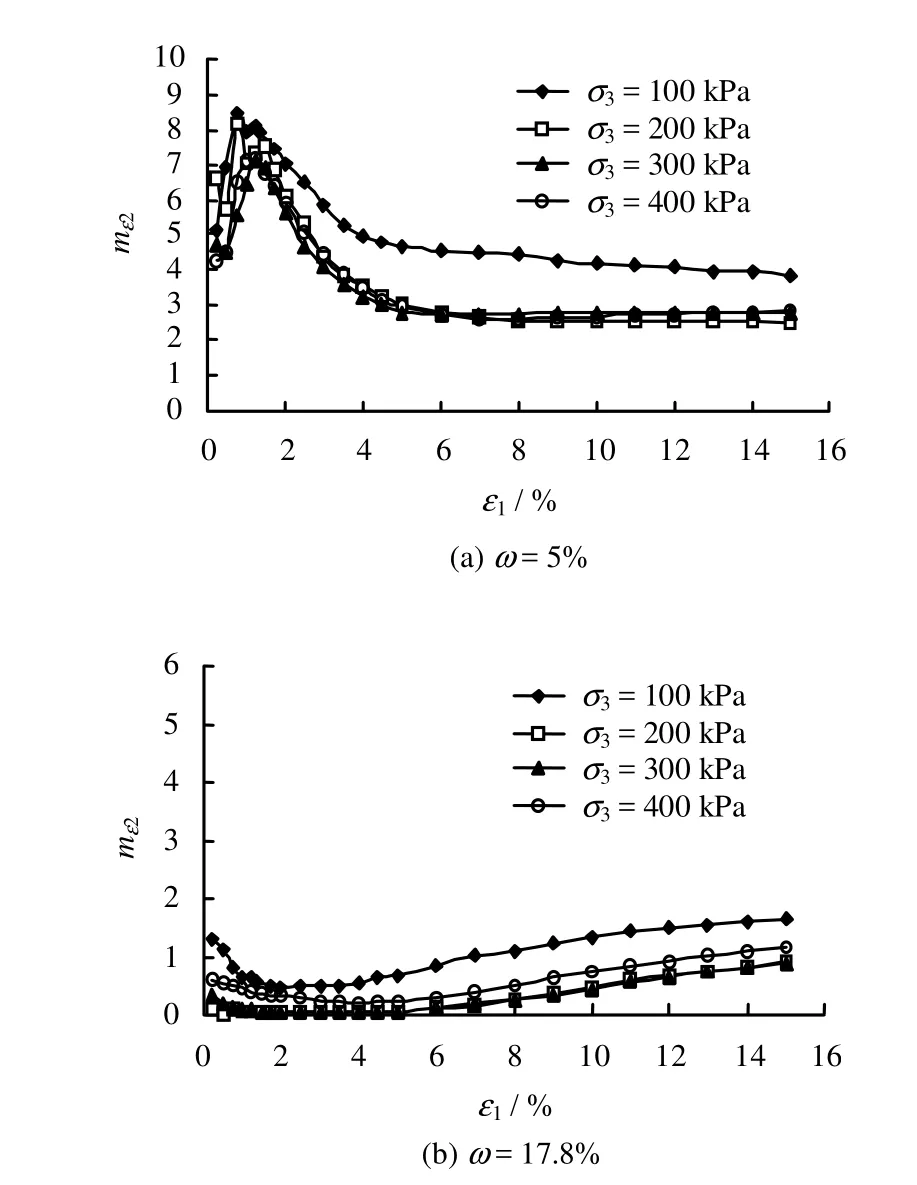
圖4 重塑黃土摩擦結構靜力強度勢參數曲線(ρd=1.26 g/cm3）Fig.4 Curves of friction structural static strength potential parameter for remolded loess (ρd=1.26 g/cm3)

圖5 不同含水率重塑黃土摩擦結構靜力強度勢參數平均值曲線（ρd=1.26 g/cm3）Fig.5 Curves of friction structural static strength potential parameter for remolded loess under different water contents (ρd=1.26 g/cm3)

4.3 黃土結構靜力強度勢分析

圖6(a)、6(b)分別為不同含水率條件下的原狀黃土結構靜力強度勢參數曲線。從圖中可以看出：①隨著應變的增大，原狀黃土的結構靜力強度勢參數在小應變（ε1＜4%）時快速減小，應變較大時減小速度放緩，最后趨于平穩。這表明：黃土結構的損傷破壞主要發生在小應變階段，結構損傷破壞的速度隨著應變的增加逐漸減緩，結構性逐漸減弱。②同一含水率、不同圍壓下原狀黃土結構靜力強度勢參數曲線同樣均處在一較窄的條帶范圍內即結構靜力強度勢參數數值比較接近，表明結構靜力強度勢參數受圍壓的影響較小，本文所提出的結構靜力強度勢參數對不同圍壓有較好的歸一性，顯示出較好的穩定性。

圖6(c)為水泥人工結構性黃土的結構靜力強度勢參數曲線。可以看出：隨著應變的增大，結構靜力強度勢參數mε在小應變（ε1＜2%）時快速減小，應變較大時減小速度放緩，最后略有增加，這種后期略有增大的趨勢也是由于摩擦結構靜力強度勢參數的變化趨勢所引起的。②不同周圍壓力下人工結構性黃土的結構靜力強度勢參數曲線同樣均處在一較窄的條帶范圍內（除σ3=100 kPa的結構靜力強度勢參數曲線稍高外）即結構靜力強度勢參數數值比較接近。表明水泥人工結構性黃土的結構靜力強度勢參數對不同圍壓有較好的歸一性，同樣顯示出較好的穩定性。

圖7為原狀黃土與人工結構性黃土的結構靜力強度勢參數平均值（4個圍壓的平均值）曲線。可以看出：含水率為ω=17.8%的不同密度和水泥含量的人工結構性黃土的結構靜力強度勢參數曲線與含水率為ω=17.8%及ω=26%的原狀黃土的結構靜力強度勢參數曲線具有相似的形態，而且兩個含水率條件的原狀黃土的結構靜力強度勢參數曲線處在人工結構性黃土的結構靜力強度勢參數曲線所在的條帶內，表明采用水泥作為膠結材料模擬原狀黃土的結構性是可行的。

圖7 原狀黃土與人工結構性黃土（ω = 17.8%）結構靜力強度勢參數平均值曲線Fig.7 Curves of structural static strength potential parameter (average) for intact loess and artificial structural loess (ω = 17.8%)

表3為不同狀態下黃土的結構靜力強度勢參數mε的最大值（4個圍壓的平均值曲線的峰值）。從表中可以看出：①含水率是影響黃土結構強度的主要因素，含水率越小，結構強度越大，結構性越強。②相同含水率條件下，干密度為ρd=1.26 g/cm3時，人工結構性黃土的結構靜力強度勢參數mε隨著水泥含量的增加而增大，表明水泥含量越高，土顆粒之間的膠結力越強，土的結構性越強，結構靜力強度勢參數mε的值就越大。

不同圍壓下某一應變時的黃土的結構靜力強度勢參數能夠準確反映該狀態下結構損傷破壞后結構強度的損失變化趨勢；某一狀態下黃土的結構靜力強度勢參數的最大值能夠代表黃土結構性的強弱，mε值越大，表明黃土的結構性越強。

表3 黃土結構靜力強度勢參數mε的最大值Table3 Maximum values of mε

5 基于強度條件的黃土靜力結構性參數的討論

基于強度條件的黃土結構性參數是通過黃土結構損傷破壞后土體強度損失的大小來反映黃土結構性強弱的。在力的作用下或在力與水的共同作用下，黃土的結構會被損傷破壞、弱化，土體的強度就會損失（減小），這部分損失或減小的強度就是聯結結構強度和摩擦結構強度。由于土體的強度、結構強度均與土體的應力狀態有關，主要受圍壓的影響，因此，為了準確反映黃土結構性強弱，基于強度條件的黃土結構性參數均采用相同壓力狀態下飽和重塑黃土的強度（壓密強度）作為標尺來衡量黃土結構損傷破壞、弱化后土體強度損失的大小，即通過黃土的聯結結構靜力強度勢參數mε1來反映黃土聯結結構性的強弱、通過黃土的摩擦結構靜力強度勢參數mε2來反映黃土摩擦結構性的強弱、通過黃土的結構靜力強度勢參數mε來綜合反映黃土結構性的強弱。飽和重塑黃土的強度最小、最穩定，正是由于采用了飽和重塑黃土的強度（壓密強度）作為標尺，才使得相同狀態的黃土在不同圍壓下所得到的基于強度條件的黃土結構性參數具有較好一致性、穩定性。

6 結 論

（1）原狀黃土的含水率越小，黃土顆粒之間的聯結力和摩擦力均越大，聯結結構靜力強度勢參數mε1、摩擦結構靜力強度勢參數mε2以及結構靜力強度勢參數mε均越大，其結構性越強；結構性越強，結構破壞后土體強度損失越大，反之，越小。

（2）黃土結構的損傷破壞主要發生在小應變階段，隨著應變的增加結構損傷破壞的速度逐漸放緩，因此，結構性參數開始減小較快，最后逐漸趨于平穩或略有增大。

（3）人工結構性黃土的結構靜力強度勢參數mε隨著水泥含量的增加而增大，表明水泥含量越高，土顆粒之間的膠結力越強，土的結構性越強，結構靜力強度勢參數mε的值就越大。

（4）采用水泥作為膠結材料，通過調節人工結構性黃土的水泥含量和含水率來模擬原狀黃土的結構性是可行的。

（5）基于強度條件的黃土結構性參數對不同圍壓有較好的歸一性，顯示出較好的穩定性。

[1]沈珠江. 土體結構性的數學模型——21世紀土力學的核心問題[J]. 巖土工程學報,1996,18(1): 95－97.

[2]GAO Guo-rui. Classification of microstructures of loess in China and their collapsibility[J]. Science in China,Ser.A,1981,(7): 962－974.

[3]高國瑞. 中國黃土微結構[J]. 科學通報,1980,(20): 945－948.

[4]高國瑞. 黃土顯微結構分類與濕陷性[J]. 中國科學 A輯,1980,(12): 1203－1208.

[5]苗天德,王正貴. 考慮微結構失穩的濕陷性和黃土變形機理[J]. 中國科學(B輯),1990,(1): 86－89.

[6]王蘭民,鄧津,黃媛. 黃土震陷性的微觀結構量化分析[J]. 巖石力學與工程學報,2007,26(增刊1): 3025－3031.WANG Lan-min,DENG Jin,HUANG Yuan. Quantitative analysis of microstructure of loess seismic subsidence[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(Supp. 1): 3025－3031.

[7]陳正漢,方祥位,朱元青,等. 膨脹土和黃土的細觀結構及其演化規律研究[J]. 巖土力學,2009,30(1): 1－11.CHEN Zheng-han,FANG Xiang-wei,ZHU Yuan-qing,et al. Research on meso-structures and their evolution laws of expansive soil and loess[J]. Rock and Soil Mechanics,2009,30(1): 1－11.

[8]謝定義,齊吉琳,張振中. 考慮土結構性的本構關系[J].土木工程學報,2000,33(4): 35－41.XIE Ding-yi,QI Ji-lin,ZHANG Zhen-zhong. Constitutive relationship considering soil structure[J]. China Civil Engineering Journal,2000,33(4): 35－41.

[9]謝定義,齊吉琳,朱元林. 土的結構性參數及其與變形強度的關系[J]. 水利學報,1999,30(10): 1－6.XIE Ding-yi,QI Ji-lin,ZHU Yuan-lin. The parameter of soil structure and the relationship of it with deformation and strength of soil[J]. Journal of Hydraulic Engineering,1999,30(10): 1－6.

[10]謝定義,齊吉琳. 土結構性及其定量化參數研究的新途徑[J]. 巖土工程學報,1999,21(6): 651－656.XIE Ding-yi,QI Ji-lin. New path of research on soil structure and its quantitative parameter[J]. Chinese Journal of Geotechnical Engineering,1999,21(6): 651－656.

[11]邵生俊,周飛飛,龍吉勇. 原狀黃土結構性及其定量化參數研究[J]. 巖土工程學報,2004,26(4): 531－636.SHAO Sheng-jun,ZHOU Fei-fei,LONG Ji-yong.Structural properties of loess and its quantitative parameter[J]. Chinese Journal of Geotechnical Engineering,2004,26(4): 531－636.

[12]邵生俊,龍吉勇,于清高,等. 濕陷性黃土的結構性參數本構模型[J]. 水利學報,2006,37(11): 1315－1322.SHAO Sheng-jun,LONG Ji-yong,YU Qing-gao,et al. A constitutive model of collapsible loess with structural parameter[J]. Journal of Hydraulic Engineering,2006,37(11): 1315－1322.

[13]陳存禮,胡再強,高鵬. 原狀黃土的結構性及其與變形特性關系研究[J]. 巖土力學,2006,27(11): 1891－1896.CHEN Cun-li,HU Zai-qiang,GAO Peng. Research on relationship between structure and deformation property of intact loess[J]. Rock and Soil Mechanics,2006,27(11): 1891－1896.

[14]駱亞生,謝定義,邵生俊,等. 復雜應力狀態下的土結構性參數[J]. 巖石力學與工程學報,2004,23(24): 4248－4251.LUO Ya-sheng,XIE Ding-yi,SHAO Sheng-jun,et al.Structural parameter of soil under complex stress conditions[J]. Chinese Journal of Rock Mechanics and Engineering,2004,23(24): 4248－4251.

[15]駱亞生,謝定義. 復雜應力條件下土的結構性本構關系[J]. 四川大學學報(工程科學版),2005,37(5): 14－18.LUO Ya-sheng,XIE Ding-yi. Structural constitutive relation of soils under complex stress conditions[J].Journal of Sichuan University (Engineering Science Edition),2005,37(5): 14－18

[16]田堪良. 黃土的結構性及其結構性本構關系研究[D].南京: 河海大學,2009.