唐-曹高速公路軟土的微結構特征研究

母煥勝

（河北省交通規劃設計院，石家莊 050011）

1 前 言

河北省沿海地區廣泛分布厚層海積軟土，屬于典型的濱海相——海陸交互相沉積所形成的軟土地基，對軟土地基處理技術研究己成為改善投資環境、加快環渤海地區建設、科學合理利用土地資源的重要研究課題。軟土地基處理方法的科學合理與否，關鍵是從軟土本身的結構特征揭示出影響軟土變形和強度的本質因素，建立軟土微結構特征與宏觀性質的關系，進而對沿海地區軟土地基處理方法進行分析評價，并提出新的技術方法。

隨著土力學理論和土體測試技術的進步和發展，人們逐漸認識到軟土是一種具有特殊結構的地質體，其物質的組成和結構共同決定著它的工程特性，即從微觀領域和從本質上揭示出軟土的變形和強度特征[1]。因此，應用軟土微結構特征、結構強度等理論，建立結構性本構模型，使軟土的研究理論和方法提高到一個新的水平。胡瑞林等[2]以Housdoff分維計算方法為主，獲得了顆粒分布及其大小和表面特征分維以及空隙與接觸帶分布分維的定量結果，并分析了這些參數與土的工程性質之間的關系。正如沈珠江院士[3]指出的“發展和建立土的結構模型和相應的分析理論，是 21 世紀土力學的核心問題”。理論的進步必將推動實踐的發展，深入開展軟土結構性研究的理論成果必將推進對軟土工程實踐向更科學化、合理化發展。

唐-曹高速公路是唐山市至曹妃甸工業區最快捷便利的高速通道，向南與河北省高速公路網中的“橫三”沿海高速公路連接，向北與G25長深高速公路相連接，在唐山市“一縱兩橫三條線”新型高速公路網絡的形成起到了重要作用。它的建成拉動了唐山區域經濟的發展，促進了公路沿線旅游資源的開發和利用，展現了中國北方最大、最現代化的曹妃甸工業大港的風采。高速公路通過地區廣泛分布著厚層海積軟土，屬于典型的濱海相～海陸交互相沉積所形成的軟土地基。

本課題以唐-曹高速公路通過地區的海積軟土為研究對象，綜合海積軟土的基本物理力學性質和微結構特征，建立了軟土微結構定量化參數。通過室內試驗和理論分析，系統地分析和研究海積軟土微結構與宏觀力學性質關系，對海積軟土的結構強度與工程效應進行了分析論證，提出以建立在分維分形理論基礎上的孔隙結構因子 PSF 作為衡量海積軟土結構強度和破壞趨勢的綜合性參數。

2 河北沿海軟土微結構分型參數特征

2.1 樣品的制備與圖像處理

幾乎所有微觀組構的技術都不能直接測定潮濕的未擾動海積軟土樣，而需要將土中的水分進行置換或排除，此過程中土的原始組構不可避免的受到影響，如何選擇恰當的脫水技術，減少對樣品的擾動就至關重要。現有的脫水技術主要有干燥 法、風干或烘干法、臨界點干燥法和冷凍干燥法等。這些方法中，臨界點干燥法和冷凍干燥法對設備要求高、操作比較復雜，但其對土樣擾動小，更能反映土組構的原始形態。因此，本研究所用土樣在干燥時均采用冷凍干燥法處理。所用儀器為中國科學院廣州地球化學研究所研制的土微結構真空冷凍制樣儀，事先將原狀土用細鋼絲鋸切成4 mm×4 mm×10 mm 的土條，放入沸點為-140 ℃的異戊烷中，再將裝有樣品的異戊烷容器放入液氮（沸點為-190℃）中冷凍，使土中的液體成為不具膨脹性的非結晶態冰，然后，在-50 ℃的狀態下對其抽真空15 h以上，使土中非結晶的冰直接升華，從而使土樣既干燥又不變形，采用掃描電子顯微鏡對所制備土樣組構的觀察以及定量化研究。

試驗中，采用德國LeicaQwin5000偏光圖像處理系統對 SEM 拍攝的照片處理，并用LeicaQwin5000偏光圖像處理系統及 FIPS（fractal image process system）分維圖像處理軟件，對處理后所得的圖像進行分析。對輸入圖像進行二值化處理后，再通過LeicaQwin中的Field（域）和Feature（特征塊）測量工具，對圖像中的孔隙部分進行統計和計算，得到土中孔隙大小、形態、排列特征等一系列微觀結構參數，用FIPS (fractal image process system）分維圖像處理軟件得到一系列關于土中孔隙的分形參數。這些結構參數從不同方面反映了軟土在變形過程中孔隙的形態特征、排列特征以及其他相應的變化特征。

2.2 微結構定量化參數

微結構量化參數有等效直徑、面積比、充填比和各向異性率。

（1）等效直徑D

等效直徑 D是與孔隙面積相等的等效圓的直徑：

式中：A為孔隙的實際面積。

（2）面積比：

面積比是所測孔隙面積占總圖像面積的百分比，也稱平面孔隙率：

式中：A1為顆粒與孔隙的總面積。

（3）充填比：

充填比是實測孔隙面積與其外接圓面積比的平方根：

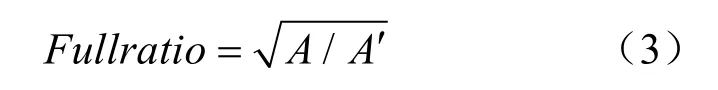
式中：A′為孔隙的外接圓面積。充填比值越大，說明孔隙越趨于呈圓形

（4）各向異性率In[4]：

In反映土微觀結構孔隙排列的整體定向性特征，是表達變形過程中整個微結構變化的重要參數：

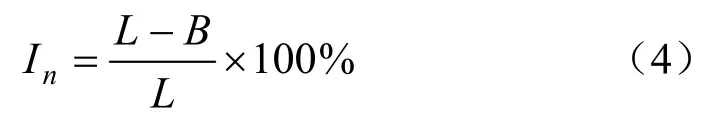
式中：L、B分別為孔隙的長軸和短軸的長度。各向異性率值的變化范圍在0～100 %之間，當In= 0時，孔隙呈隨機分布；當In= 100%時，孔隙呈同一方向分布。

2.3 孔隙的分形參數

簡單分形維數Dp是一個無量綱、無標度的量，它減弱了微觀圖像的分辨率、放大倍數等對計算結果的影響，表示在某種意義上的層次性和自相似性，用計盒維數來估計。

如圖1所示，假設圖像中含有多個孔隙（點狀閉域），以邊長為 ε的正方形將圖像分割成規格為(L／ε)×(L／ε)的正交網格，并且，設含有孔隙（或一部分）的網格總數為 N(ε)，如果改變 ε，使其在值域范圍內序列變化，如ε1，ε2，…，εn，則得到相應的序列值 N(ε1)，N(ε2)，…，N(εn)，將這些數據組描繪于雙對數坐標系中，即可直觀確定 lgε-lgN(ε)對應關系。

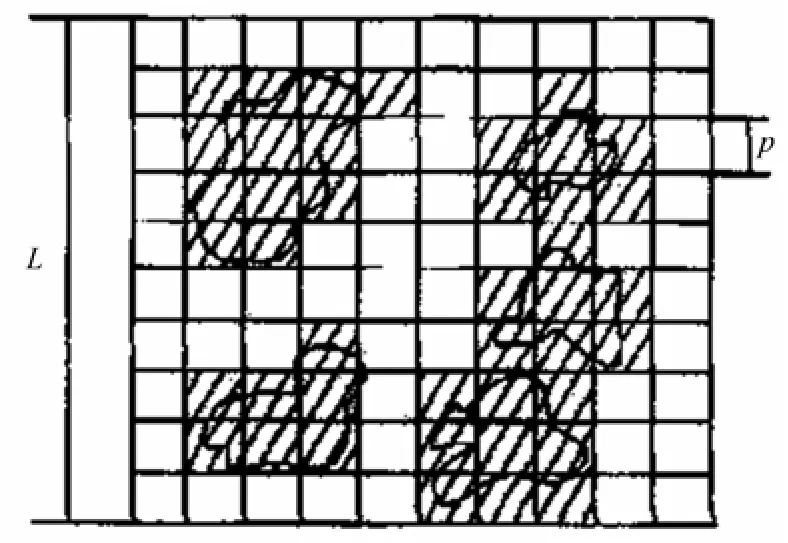
圖1 計盒維數算法Fig.1 Algorithm of box counting dimension

如果存在線性特征，表明孔隙分布具有分形特征，若線性部分的斜率為k，那么

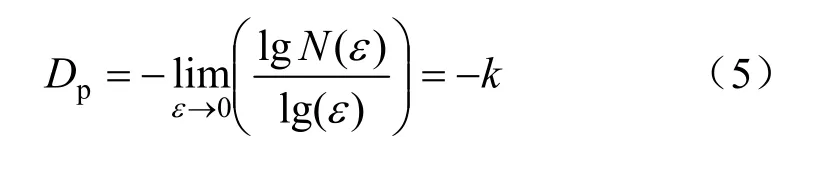
平面分維值 Dp越大，表明孔隙分布越均勻，顆粒集團化程度越低，土的密實度越小。

2.4 簡單分形維數Dp與壓力的關系

用 FIPS 對曹妃甸區、唐海區、南堡區原狀樣及不同荷載作用后土樣的 SEM 照片進行處理后，所得三個區軟土原狀樣及其在不同壓力作用下土樣中孔隙平面分維值見表1。

表1 軟土原狀樣及不同壓力下孔隙簡單分維數DpTable1 Dpof the soft soil undisturbed sample at different pressures

由計算所得各土樣的孔隙平面分維值繪出的曹妃甸區、唐海區、南堡區（垂直截面與水平截面）的軟土孔隙平面分維值Dp隨壓力 P的變化曲線如圖2所示。孔隙的平面分維數反映土中孔隙的分布情況和密實情況，其值越大，土樣越松散，密實度越小。由圖可見，（l）三個區軟土原狀樣在垂直截面上的孔隙平面分維值，曹妃甸區較小，其值為1.888；唐海區較大，其值為1.925；南堡區處于兩者之間，為1.913，說明三個區原狀土中，唐海區土最為松散，孔隙所占比例較大，土體的密實度較小；曹妃甸區土相對密實，孔隙所占比例小；南堡區則處于兩者之間。（2）三個區軟土孔隙平面分維值均與荷載有良好的相關性,在荷載作用下,三個區軟土垂直截面上孔隙平面分維值均呈減小趨勢。荷載作用初期，孔隙平面分維值變化不明顯，當荷載增加到200 kPa時，三個區軟土孔隙平面分維值均明顯的降低，曹妃甸區的值下降的幅度最大；當荷載增加到300 kPa時，分維值變化比較平緩，隨著荷載的不斷增大，孔隙的平面分維值降低。這種變化規律反映出，在壓力小于土的結構屈服壓力 時，土中孔隙含量及分布狀況變化較小；當壓力超過土結構屈服壓力后，土的結構強度大幅度損失，伴隨著土中大孔隙的坍塌，孔隙含量急劇減小，隨著荷載的不斷增大，土中孔隙不斷被壓密，土的密實度提高。（3）南堡區軟土在水平截面上的孔隙平面分維值隨荷載的變化趨勢與垂直截面土的變化規律基本一致,但在水平截面上孔隙分維值隨荷載的變化幅度要小，在曲線上則表現為水平截面上分維值與荷載的變化曲線在垂直截面的上方，這說明荷載的作用對于土水平截面的影響要小于對垂直截面的影響。

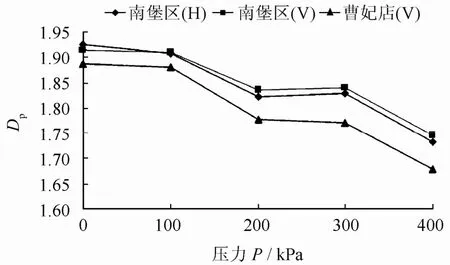
圖2 三個區軟土水平截面上Dp-P關系曲線圖Fig.2 Curves of horizontal section of the soft soil of three areas Dp-P relation

2.5 多重分形譜-壓力的關系

用 FIPS 對曹妃甸區、唐海區、南堡區原狀樣及不同荷載作用后的土樣的SEM照片進行處理后，三個區孔隙多重分形譜各特征參數f(α)見表2、3。表中，Δα為分形譜寬度；f為孔隙分形譜。海積軟土孔隙多重分形譜的形狀與土中孔隙的特征密切相關，而土中孔隙又從根本上決定了概率分布，因此，不同地區、不同狀態的土中孔隙多重分形譜的形狀反映了其各自的孔隙概率分布特征。所研究的材料不同或材料的特征不同時，多重分形譜的形狀還有可能呈右鉤狀或鐘狀。

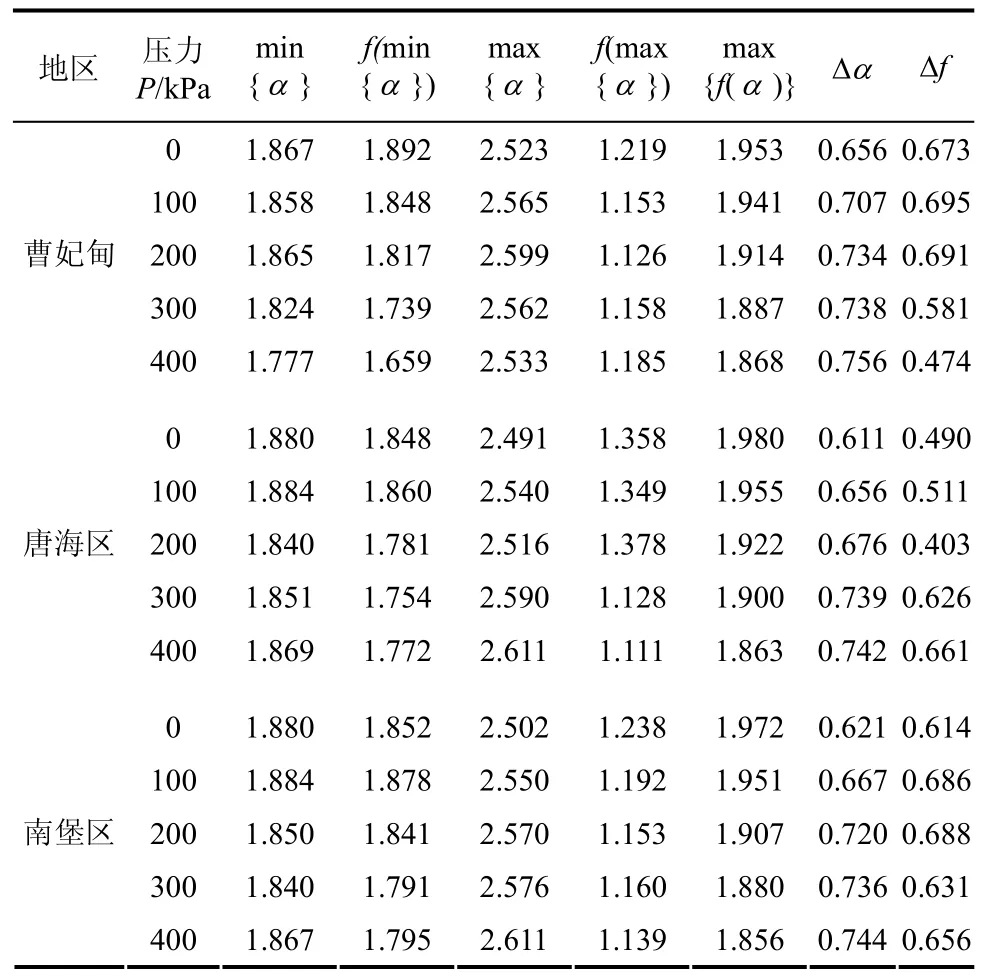
表2 軟土原狀樣在不同壓力下垂直截面上f(α)值Table2 f(α)of the soft soil undisturbed sample in vertical section at different pressures

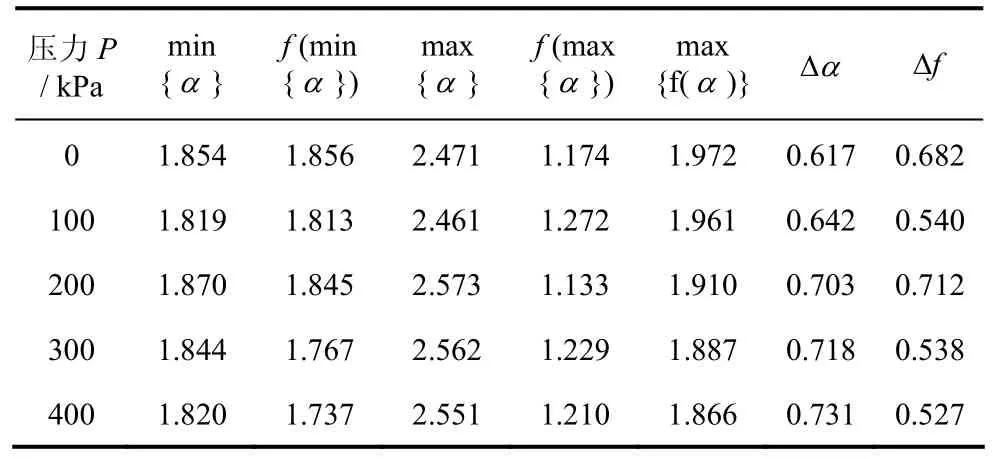
表3 南堡區軟土原狀樣及不同壓力下水平截面上f(α)Table3 f(α) of the soft soil undisturbed sample in horizontal section of Nanpu at different pressures

由所得的各土樣的孔隙多重分形特征參數，繪出的曹妃甸區、唐海區、南堡區（垂直截面與水平截面）軟土中孔隙分布平面分維最大值maxf(α)隨壓力的變化可見，（1）maxf(α)反映的是概率分布中最或然子集的性質，在土微觀孔隙多重分形譜中則反映的是土中孔隙含量最多的區域的性質。對比三個區軟土原狀樣在垂直截面上的孔隙分形譜最大值maxf(α)可知，唐海區最高，其值為1.98；曹妃甸區最低，其值為1.953；南堡區處于兩者之間，為1.972，說明對于三個區原狀土中孔隙含量最多的單元而言，唐海區軟土較為松散，孔隙所占比例較大，曹妃甸區軟土孔隙含量相對較低，南堡區則處于兩者之間。（2）三個區軟土在垂直截面上孔隙分布平面分維最大值隨著荷載的增加均呈降低的趨勢，說明土中孔隙所占的比例在荷載作用下不斷減小。（3）南堡區軟土在水平截面上的孔隙分布平面分維最大值隨荷載的變化趨勢與垂直截面上的變化規律基本一致，但水平截面上孔隙maxf(α)隨荷載的變化與垂直截面上相比，變化幅度要小，說明荷載的作用在水平截面上對于土中孔隙含量最多的區域的性質的影響要小于在垂直截面L的影響。（4）孔隙的分形譜最大值maxf(α) 反映的是土中孔隙含量最多的區域的性質；孔隙簡單平面分維數 Dp反映的是土中孔隙整體上的含量情況。三個地區（垂直截面與水平截面）軟土中孔隙分形譜寬度Δα隨壓力的變化曲線如圖3所示。

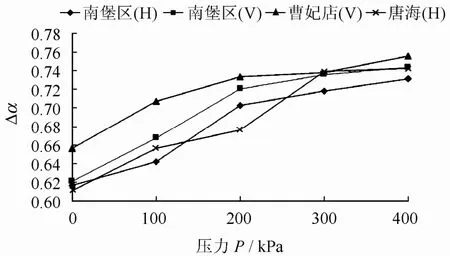
圖3 三個區軟土中Δα-P關系圖Fig.3 Curves of Δα-P relation graph of pore in three areaes

分形譜寬度Δα反映的是概率分布范圍的大小，在土微觀孔隙多重分形譜中則反映的是土中孔隙分布的均勻化程度，土中孔隙概率分布越不均勻，相應的Δα越大。對比三個區軟土原狀樣在垂直截面上的孔隙的分形譜寬度可知，曹妃甸區最大，為0.656；唐海區最小，為0.611；南堡區處于兩者之間，并與唐海區接近，其值為0.621，說明曹妃甸區軟土中孔隙分布的均勻化程度較低，唐海區軟中孔隙概率分布較均勻，南堡區處于兩者之間。

三個區軟土在垂直截面上孔隙多重分形譜寬度隨著荷載的增加均均非線性增大，且在較高荷載作用下，分形譜寬度△α沒有明顯的差別,說明土中孔隙概率分布的均勻化程度在荷載作用下不斷降低，且隨著荷載的不斷增大，三個區軟土中孔隙分布的均勻化程度差距減小。

南堡區軟土在水平截面上的孔隙多重分形譜寬度隨荷載的變化趨勢與垂直截面上的變化規律基本一致，但在水平截面上孔隙的 Δα隨荷載的變化與垂直截面上相比，變化趨勢較緩，說明在荷載作用下，水平截面上孔隙概率分布的均勻化程度變化幅度要小于垂直截面上孔隙概率分布的均勻化程度。

2.6 軟土結構因子-壓力的關系

對土中孔隙的平面分維研究表明，平面分維能很好的描述在荷載作用下土中孔隙的整體分布情況及土的密實程度,但它并不能反映孔隙的形狀，大小等其他因素。運用統計理論中的數學規劃技術對表示孔隙的大小、形狀等形態參數，以及定向性參數、孔隙的平面分維數進行綜合分析研究發現，對描述孔隙的各微觀結構參數進行組合后，所得組合參數PSF 值與壓力P具有良好的相關性，公式為

式中：PSF為孔隙結構因子；R為所用顯微鏡的分辨率，本次研究所采用的德國LEO-1530VP掃描電子顯微鏡R = 10-3μm；D為平均等效直徑；F為充填比；In為各向異性率；Dp為平面分維數。

由式（6）計算的三個地區軟土孔隙結構因子PSF值見表4和表5。根據表中三個地區軟土孔隙結構因子的計算結果繪出各區孔隙結構因子PSF隨壓力的變化關系，如圖4所示。由曹妃甸、唐海、南堡區海積軟土孔隙結構因子PSF隨壓力的變化關系可以看出，曹妃甸區、唐海區、南堡區孔隙結構因子 PSF-P 關系有以下特征：（l）孔隙結構因子PSF 與荷載P具有很好的相關性。（2）初始狀態下，唐海區軟土孔隙結構因子最大，曹妃甸區軟土孔隙結構因子最小，南堡區處于兩者之間。在荷載作用初期，孔隙結構因子變化較小，當壓力超過土結構屈服壓力以后，孔隙結構因子大幅度下降，隨著荷載的不斷增大，結構因子減小幅度變緩，三個區孔隙結構因子的差異越來越小。（3）南堡區軟土水平截面上的孔隙結構因子在荷載作用下其變化幅度相對垂直截面上而言要小。

由以上分析可知，（1）孔隙結構因子所反映的土中孔隙在荷載作用下的變化規律與其他各微觀孔隙參數（孔隙平均直徑、平面分維值等）所反映的規律一致；（2）孔隙結構因子是一個有效反映海積軟土微觀結構孔隙特征的綜合性參數；（3）孔隙結構因子的物理意義在于對于海積軟土而言，孔隙結構因子越大，土體破壞的趨勢越大；海積軟土孔隙結構因子越大，土的結構強度越低，這也從另一個方面證明了曹妃甸區海積軟土相對較穩定，其結構強度要高于南堡和唐海區軟土。

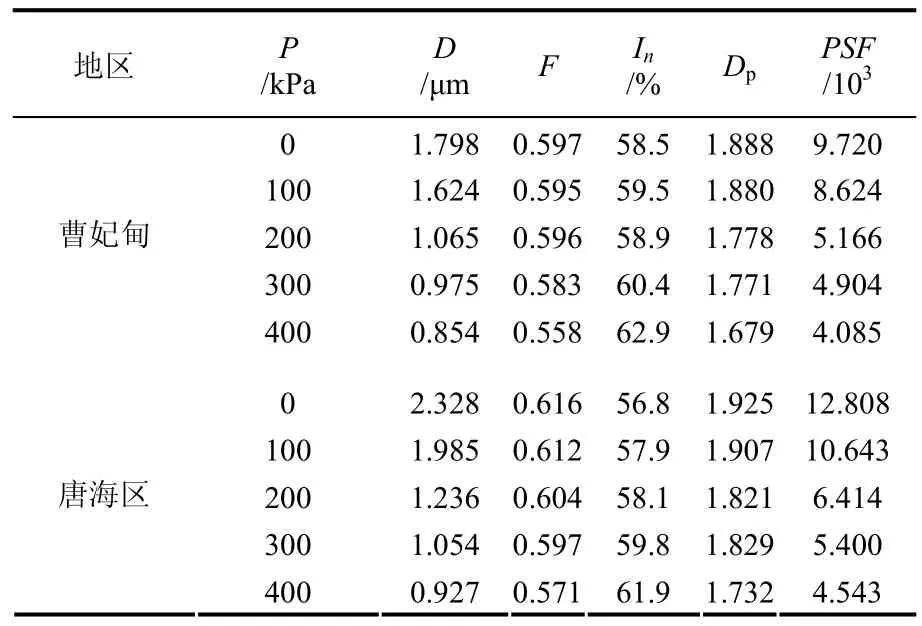
表4 海積軟土原狀樣及不同壓力下垂直截面上PSF值Table4 The PSF of the marine deposited soft soil undisturbed sample in vertical section at different pressures

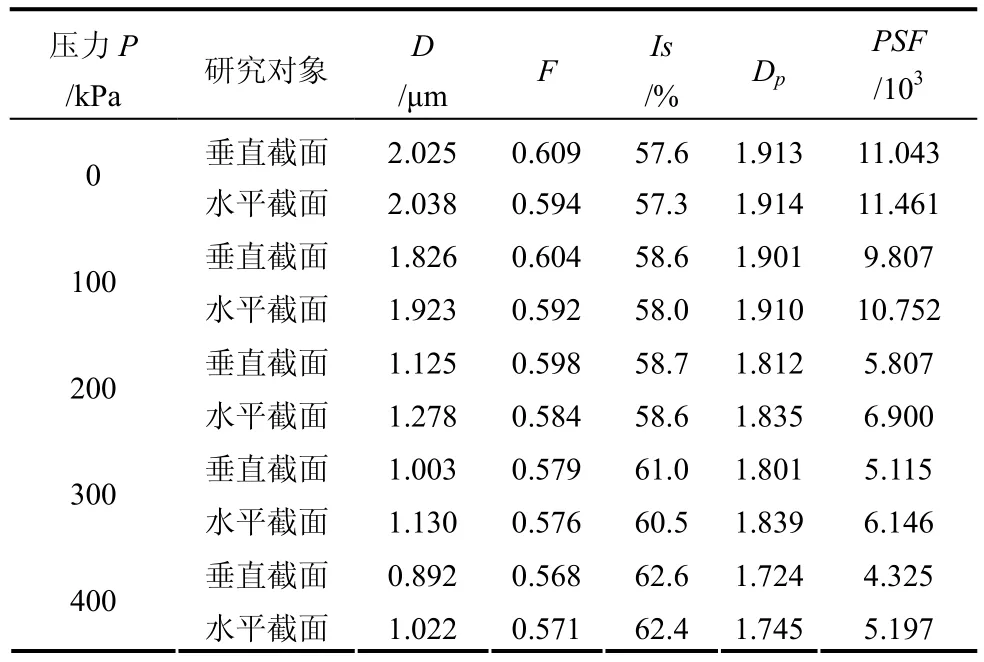
表5 南堡區海積軟土原狀樣及不同壓力下垂直截面與水平截面上PSF值Table5 The PSF of the marine deposited soft soil undisturbed sample in vertical section and of Tanghai at different pressures

圖4 三個區垂直截面上PSF-P關系圖Fig.4 Curves of PSF-P relation about three areas in vertical section

3 沿海軟土的結構強度

土結構性的存在使得天然沉積的軟黏土一般都具有結構強度，許多學者的研究結果表明，由于一般土都具有結構性，特別對于具有較強結構性的軟土而言，用傳統的 Casagrande 法等方法在壓縮曲線上用作圖法確定出來的值并非是其真正的先期固結壓力，而是其結構屈服壓力，它是先期固結壓力與結構強度之和，因此，若要確定軟土的結構強度，需先確定其相應的先期固結壓力。

王國欣[5]用重塑土建立的還原后壓縮曲線的數學模型為

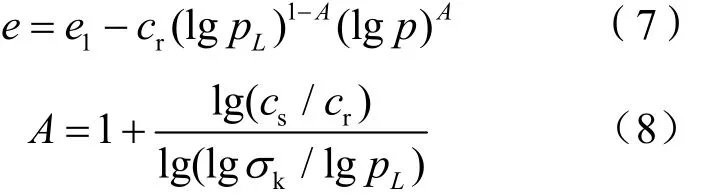
式中：e1為壓力為1 kPa 時對應的孔隙比，可有初始孔隙比e0代替；cr為理想重塑樣的壓縮指數，即理想重塑樣壓縮曲線的斜率；cs為重塑樣回彈指數，即重塑樣回彈滯回圈端點連線的斜率；σk為原狀樣的結構屈服壓力；pL為重塑樣與原狀樣壓縮曲線交點L所對應的壓力值；A為還原系數，它反映了還原后壓縮曲線的特征。

王國欣建議對欠固結狀態上而言，把李濤[6]模型中的上覆壓力p0參數換成了結構屈服壓力σk。由于李濤擾動土的模型已經過許多試驗的檢驗，而王國欣針對重塑上還原的模型只是對李濤模型的改進和簡化，具有較高的可靠性。

3.1 軟土壓縮曲線特性

為了確定沿海地區軟土的先期固結壓力以及相應的結構強度，分別對曹妃甸、南堡、唐海三個區取樣深度均為10 m的全新世中期（Q42 m）的海相淤泥質粉質黏土進行了單向壓縮試驗，三個區軟土壓縮曲線形態基本相似，曹妃甸區的原狀樣和重塑樣的壓縮曲線如圖5所示。

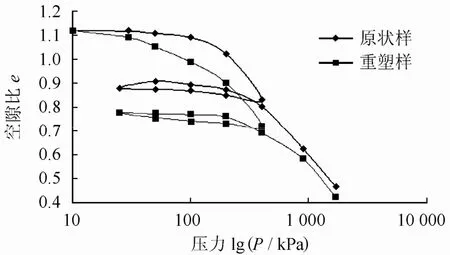
圖5 曹妃甸區軟土原狀樣和重塑樣的e-lgP曲線Fig.5 The e-lgP curves comparison chart of undisturbed sample and remodeling sample of soft soil in Caofeidian

從圖5試驗曲線可以看出，在原狀樣壓縮曲線上有一明顯的拐點，由卡氏法確定該土的結構屈服壓力為σk，在壓力低于結構屈服壓力時，曲線變化比較平緩，當壓力超過結構屈服壓力時出現陡降段，最后與重塑土的壓縮曲線趨于重合。重塑樣的壓縮曲線幾乎成線性分布，沒有明顯的轉折點，說明此時土的結構強度幾乎已經完全喪失。

3.2 先期固結壓力

根據以上曲線特征，運用王國欣改進的對于重塑土還原的數學模型，對曹妃甸區軟土的先期固結壓力進行求取。計算過程為：

①用室內壓縮試驗測出重塑樣壓縮曲線和回彈曲線，求得理想重塑土的cr= 0.43，cs= 0.058，所對應的壓力值PL= 2900 kPa。

②己知e0= l.12，σk= 195 kPa，將所得的數值代入式（7）和式（8），算出重塑土還原后的壓縮曲線，最后得到曲線的方程為

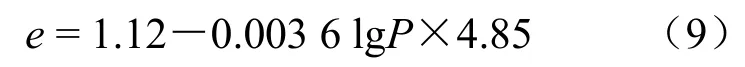
③用Casagrande法在還原后的壓縮曲線上確定先期固結壓力的值pc= 170 kPa，經計算其上覆壓力p0= 174 kPa，此軟土為弱欠固結土。

用同樣的方法計算得出與曹妃甸區同深度的南堡區、唐海區軟土的先期固結壓力，其先期固結壓力值見表6。

表6 軟土先期固結壓力值Table6 The preconsolidation pressure of soft soil

3.3 軟土結構強度的確定

結構性土的結構屈服壓力是先期固結壓力與結構強度之和，對結構性土而言，確定了土的先期固結壓力之后，就可以確定其相應的結構強度。表7給出了曹妃甸、唐海、南堡三個區取樣深度均為10 m的軟土的結構強度值。

表7 軟土的結構強度值Table7 Structural strength of soft soil

軟土原狀樣曲線與重塑樣還原后的壓縮曲線之間存在著一個差距，這個差異即是結構強度區域，代表的是在不同荷載作用下結構強度的變化規律。可以分別在重塑樣還原后的壓縮曲線和原狀樣壓縮曲線上找出同一孔隙比下所對應的壓力值的大小，其差值正反映了此孔隙比下的土的結構強度的大小。

隨著壓力的增大，土的結構性會逐漸破壞，結構強度也隨之降低，最后完全喪失，使土最終成為重塑土。在壓縮曲線上表現為原狀樣的壓縮曲線和重塑樣還原后的壓縮曲線最終趨于重合。分析總結出這樣的規律：當壓力小于結構屈服壓力時，土的結構損傷很小，可以認為土的結構強度基本保持不變；當壓力大于結構屈服壓力時，結構強度隨壓力的增大迅速降低，使土最后趨于重塑土的性狀。

4 結 論

（1）將多重分形算法引入到土微觀結構研究中，對沿海地區軟土孔隙的多重分形特征進行研究，提出了一個有效反映海積軟土孔隙破損趨勢的評價指標即孔隙結構因子PSF作為衡量海積軟土結構強度和破壞趨勢的綜合性參數。孔隙結構因子的物理意義在于：對于海積軟土而言，孔隙結構因子越大，土體破壞的趨勢越大：海積軟土孔隙結構因子越大，土的結構強度越低。這也從另一個方面證明了曹妃甸區海積軟土相對較穩定，其結構強度要高于南堡和唐海區軟土。

（2）由于軟土存在顯著的結構強度，用傳統的求取先期固結壓力的方法所得到的壓力并非結構性土的真正先期固結壓力，而是其結構屈服壓力。求解先期固結壓力的同時，可以定量地確定土的結構強度，對曹妃甸、唐海、南堡三個地區同一深度的土進行結構強度求取結果顯示，曹妃甸區軟土結構強度較高，唐海區軟土結構強度相對較低，而南堡區處于兩者之間。

[1]塔薩奇,潑克. 蔣彭年譯. 工程實用土力學[M]. 北京:水利電力出版社,1960.

[2]胡瑞林,官國琳,李向東,等. 黏性土微觀結構定量模型及其工程地質特征研究[M]. 北京: 地質出版社,1995.

[3]沈珠江. 土體結構性的數學模型—21世紀土力學的核心問題[J]. 巖土工程學報,1996,18(1): 95－97.SHEN Zhu-jiang. The problem of constitutive model of structured soils is the focus problem of soilmechanics in the 21 century[J]. Chinese Journal of Geotechical Engineering. 1996,18(1): 95－97.

[4]施斌. 黏性土擊實過程中微觀結構的定量評價[J]. 巖土工程學報,1996,18(4): 57－62.SHI Bin. Quantitative assessment of changes of microstructure for clayey soil in the process of compaction[J]. Chinese Journal of Geotechical Engineering. 1996,18(4): 57－62.

[5]王國欣. 軟土結構性及其擾動狀態模型研究[博士學位論文D]. 沈陽: 吉林大學. 2003.

[6]李濤,錢壽易. 土樣擾動影響的評價及其先期固結壓力的確定[J]. 巖土工程學報,1987,9(5): 21－30.LI Tao,QIAN Shou-yi. Evaluation of soil sample disturbance and determination of its preconsolidation pressure[J]. Chinese Journal of Geotechical Engineering. 1987,9(5): 21－30.