優化的PFA算法在GPS軟件接收機中的應用

姚相振，崔紹龍，方金云

（1.中國科學院 計算技術研究所，北京 100190；2.中國科學院 研究生院，北京 100049）

1 引言

衛星信號捕獲是GPS接收機里的第一個必要操作，它用來檢測來自天線接收的信號中包含有哪些導航衛星的信息，捕獲的最終目的是為了得到載波的多普勒頻移以及每顆衛星C/A碼的初始相位。在此過程中執行C/A碼相位和多普勒頻移的二維搜索，具體的操作是用本地生成的碼跟接收到的信號做交叉相關，然后把相關的結果累加起來，設定一個門限，超過此門限則判定相應的衛星被捕獲。

GPS信號采用擴頻調制技術，導航數據首先被C/A碼或者P碼進行擴頻調制，然后對1575.42MHz的L1載波進行BPSK調制。同相分量上含有C/A碼，正交分量上含有P碼。因此，利用Gold碼的相關特性進行相關調制是 GPS接收機中最基本的運算。相關器的性能和C/A碼的捕獲成功率，往往決定了接收機的性能。在噪聲環境，尤其是弱信號的時候，利用相干累計和非相干累計技術可以提高接收機的增益。但是無論是相干累計還是非相干累計都包含有大量的相關運算，這對于軟件接收機來說無疑是一個沉重的負擔[1]，Van Nee在文獻[2]中提出了用FFT運算來代替相關運算，此方法大大提高了運算的效率，也奠定了軟件無線電設備的基礎，但是在軟件導航接收機中要實現實時信號處理，傳統的FFT算法還是無法勝任，另外，FFT中存在的大量浮點運算也使得在嵌入式導航接收機上更是難以實現實時性，因為市場上現有的嵌入式設備對于浮點運算的支持還不是很完善。

為了減少捕獲階段的運算復雜度以及處理時間，大量的嘗試和實驗已經被實施，在文獻[3]中提出一種平均相關算法，此算法對采樣值求平均，以降低參與 FFT/IFFT的運算點數。在文獻[4,5]中，作者提出一種自我調整捕獲方案，它能夠根據信噪比的大小自動的調節捕獲門限的大小，文獻[6]中提到了一種利用特殊軟件相關器的方法，使用并行位操作來實現 32個點同時工作來模擬硬件相關器，結果顯示其效率有很大程度的提高。

本文中提出一種優化 PFA算法，首先，提出一種基于位操作的基帶混合算法，從RF前端得到的數字信號被存儲為一種特殊的2bit形式，本地載波體也被量化為2bit形式，為2組數據創建一個數據表，通過索引來實現基帶混合的過程，避免了乘法運算，在FFT運算過程中，將旋轉因子預存為16bit的補碼形式，并將其映射為一個較大的整數，中間數據以及最終結果都用一個32bit的整數來存儲，在每一次蝶形運算后進行溢出檢測，以確保數據的正確性，另外 PFA算法過程中不必要的乘法也將會被省略，因此在整個運算過程中只存在整數運算，此方法在浮點運算支持不利嵌入式設備上的運行取得良好的運行效果。

2 信號捕獲

2.1 循環相關到FFT的演化

所有的GPS衛星都發射1.57542GHz(L1波段)和1.2276GHz（L2波段）2種頻率的信號，GPS的信號發射采用的是CDMA模式[7]，低頻的導航數據被高頻的偽隨機碼進行調制，每顆衛星的信號通過調制不同的偽隨機碼來實現身份識別，GPS信號采用了 2種不同的偽隨機碼:一種是 C/A碼（Gold碼的一種），碼片率為 1.023Mchip/s, 另一種是 P碼，碼片率為 10.23Mchip/s。P碼被調制在 L1和L2載波上，而C/A碼僅調制在L1載波上且與P碼相位相差90°。C/A碼被廣泛用于民用接收機應用，而P碼被加密為一個被稱為P(Y)碼的編碼，只用于軍事裝備。在此本文重點討論C/A碼的應用模式。

從RF前端接收到的信號可以表示為

其中，Ns代表可見衛星的個數，Ai代表信號的幅度，Di代表導航數據，Ci代表第i顆衛星的C/A碼，tτi代表碼時延，fdi代表多普勒頻移，fL1代表 L1載波的頻率，其值為1575.42MHz，fIF是RF下變頻后的中頻頻率，φi代表衛星i的初始相位，n代表一個均值為零方差為的高斯白噪聲。用于計算多普勒頻移造成的碼元長度變化。

C/A碼一個周期長度為1023個碼元，碼率為1.023MHz，一個周期的C/A碼可以用式(3)表示為

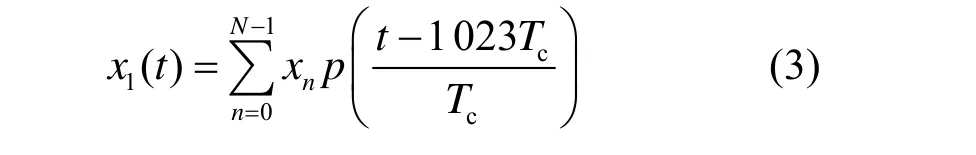
p(t)表示以原點為中心，具有單位高度和單位寬度的脈沖波形。xn為C/A碼的第n個碼元。可以用+1 和?1 來表示，Tc=1/(1.023MHz)= (1/1.023)μs，是C/A碼的碼元寬度，C/A碼的周期Tcode= 1023Tc=1ms。

在硬件GPS接收機中，由于硬件相關器的應用使得處理循環相關的速度非常快，而在軟件接收機中則是用FFT來代替相干運算以達到提速的目的。對于N點數據的離散傅里葉變換（DFT）表示如下:

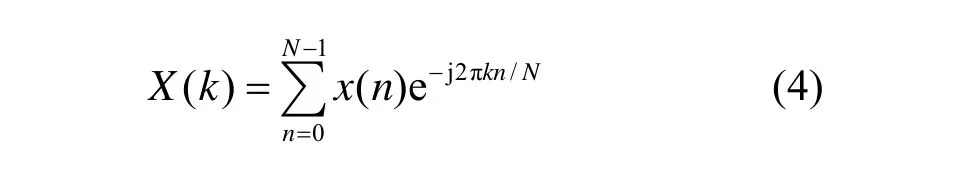
x(n) 和y(n) 2個N點有限時域信號的循環相關表達式為

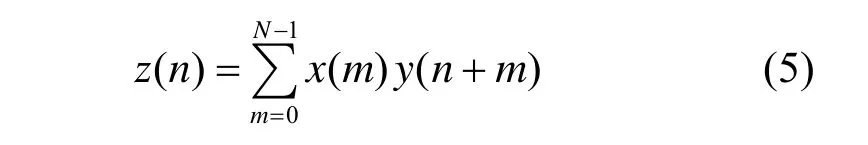
基于式(4)和式(5)推出x和y序列循環相關的DFT公式:

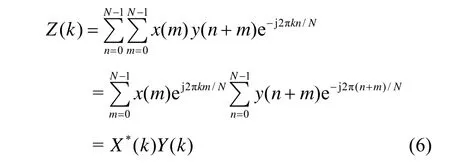
其中，* 代表復數的復共軛形式，X和Y是x和y信號的頻域表達形式。

從式(6)中可以看到x和y序列循環相關的DFT可以用X和Y的乘積來表示，見文獻[8]，其中一個是復共軛的形式。只需要對其結果做一次逆傅里葉變換(IFFT)就可以轉化為時域表示形式:

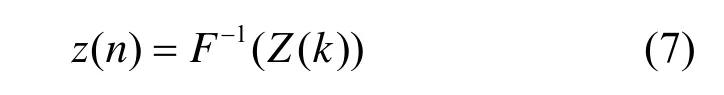
z(i)max代表 z( n)集合中最大的一個,i暗示了GPS信號C/A碼的初始相位。

本地載波信號分為同向和正交2種，載波信號跟本地C/A碼信號相乘作為整體的本地數據:

Cj代表j號衛星的C/A碼，是衛星j的估計初始相位。

2.2 循環相關過程

接收機接收到的數據跟本地數據相乘得:

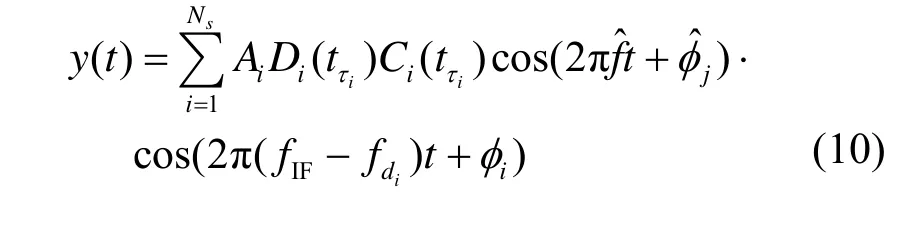
3 優化PFA算法

本文將RF前端得到的中頻信號以及本地載波信號進行量化，用特定的位格式存儲，通過移位元操作來代替原有的乘法操作，因此所有的浮點運算都被轉化為了位運算，在大多數的微處理器上，移位操作比數學運算要快得多。在PFA算法之前首先要進行基帶混合運算，將接收到的導航數據跟本地載波數據相乘；PFA算法是FFT算法的變種[9]，為了解決非基二點的數據輸入，但是對于輸入點個數也有相應的要求，必須為 m×2n的形式，其中，m為質數，n為正整數。本文根據實際情況設計了一種適用于PFA算法的插值方案。

3.1 帶通采樣定理和插值參數的選擇

對于中心頻率在0f，信號帶寬為B的中頻模擬信號，如果用采樣率為sf進行采樣量化，采樣后的信號頻譜，必然是以sf為周期，對原始模擬信號的頻譜進行周期擴展的結果。如果要求采樣后的頻譜不發生混迭，必然要求

式(11)就是帶通采樣定理的主要內容[10]。

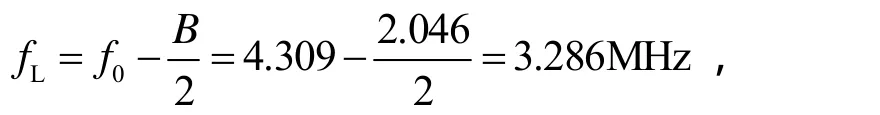
因此原始采樣頻率sf=5.714MHz是滿足帶通采樣定理的。

在捕獲時，對原始數據進行線性插值，必然會改變采樣頻率，從上面的討論可以看出，在5.332MHz ≤ fs≤ 6.572MHz 這個范圍內的采樣頻率，不會使得一個C/A碼周期（1ms）的樣點數正好等于2n。由于3×211=6144，對于這個組合數，有快速的 PFA算法，而與此相對應的采樣頻率fs= 6.144MHz ，也能滿足帶通采樣定理的要求。

3.2 基帶混合中的數據類型轉換

本文采用的RF前端為ZARLINK的GP2015，信號的十進制值為+1，?1，+3，?3，每個值存放在一個字節中，有用的信息存放在一個字節的低2bit中，本文將其先提取出來每4個存儲到一個字節中，然后以字節讀取的方式一次性讀取 4個導航數據進行處理，數字信號的 4個十進制值表示方式見表1。本地載波的同相跟正交兩路信號也被量化為2bit形式，見表2，在這種定義方式中假設本地載波信號的幅度為2.5，導航數據跟載波信號的量化值被預先存起來，用(Sign, Mag)數組表示，根據系統特定的要求，如果要進行高靈敏度處理，則可以通過增加本地載波的量化級數來實現。對于前面所述的理論推導過程，量化只是改變了數據的表示精度從而簡化運算過程以提高效率，滿足原有的理論，只是需要在PFA算法上進行運算方式的調整。

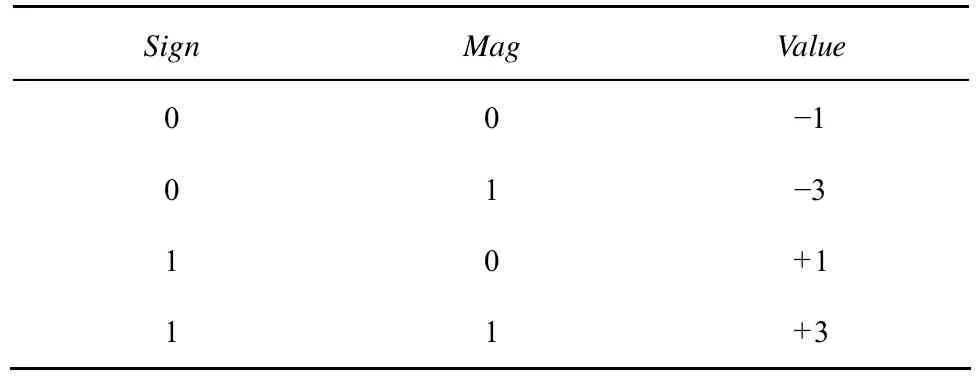
表1 導航數據的2bit量化

表2 本地載波的2bit量化

本地載波信號的頻率跟接收到的導航數據的載波頻率近似相同，然后，將接收到的數據跟本地載波的同相正交兩路信號相乘，為基帶混合過程，以實現后續的低通濾波，基于以上的2個定義，只通過(Sign, Mag)數組的異或運算就可得到結果，在此定義另一種存放結果的數據格式，見表 3，2個表中的數據相乘時，表3中的High Mag比特為表1中的Mag比特；Low Mag比特是表2中的Mag比特；Sign比特則是前面兩表中Sign比特異或運算的結果。此時將原本的浮點數乘法運算轉化為了簡單的位操作，最終結果只需一次查表便可得到。

表3 基帶混合結果查詢表

C/A碼本身就是二進制的碼流，因此不用做轉換而直接被預先存儲起來。接下來的步驟就是對接收信號與本地信號的乘積以及C/A碼分別做快速傅里葉變換。

3.3 整數化與制表法結合的PFA算法

FFT的輸入數據在前面的步驟中已經被完全整數化，本系統中采用的FFT算法都是基二時間抽取方式的，見文獻[11]，基二FFT的本質是將原始的DFT運算分割成為一系列2點DFT運算，首先將一個原始的N點DFT分裂為2個N/2點DFT運算，然后再將N/2點DFT分裂為2個N/4點DFT，如此操作直到每個DFT的操作點數減少到2，此算法要求FFT的點個數是2的整數冪。一個基二時間抽取方式FFT的蝶形運算器結構見圖1，其中，輸入數據（A, B）和輸出數據（A', B'）都是復數形式，Wn代表在FFT每個運算階段所需要的旋轉因子。本系統采用的是時間抽取的方式，在進行FFT運算之前先進行數據的逆序操作，將排好序的數據序列進行后續的2點DFT運算。

本系統的輸入數據只有如表3所示的8個值，并且都是整數形式，不需要轉換，而對于一般形式的浮點FFT輸入數據，則要先進行整形化，具體的做法可以將其擴大一定倍數轉換為整數，因為FFT算法會產生固有的處理增益，對于實數輸入，其處理增益是 N/2，對于復數輸入，其處理增益是 N，其中，N為FFT的點數，然后在每一級蝶形運算以后對中間數據進行適當縮小以防止數據溢出。這種做法對于點數比較少的FFT應用比較合適，但是當點數很大時，由于每次蝶形運算以后對中間數據的縮小會損失一定的精度，當多次縮小操作后會使得精度大幅降低，因此，本文采取了前述的量化方式，使得輸入到FFT的數據值很小，最大的模值僅為6，運算過程中出現整數越界的情況會很少，至多進行一次數據縮小處理，保證了處理精度。

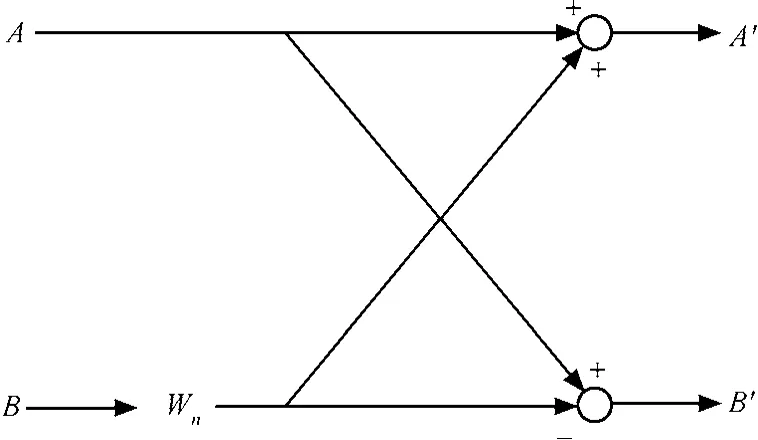
圖1 蝶形運算器結構

為了減少運算時間，旋轉因子（正弦函數以及余弦函數值）將不會被實時計算，而是預計算出來并且存儲在表格中，此表格只存儲了1/4周期的正弦函數值，用16bit二進制補碼表示，其對應的十進制的整數值代表了?1.0到1.0之間的小數。例如，在表中一個值為16384的數實際代表的值為16384/32768=0.5，其中，32768為16bit二進制補碼代表的最大正數，FFT算法需要用到正余弦函數1/2周期的值，本文中為了節省內存開銷，只存儲了1/4周期的正弦函數值，記為SinTable[]，并且每個數值都有相應的索引，在后續運算用到的正余弦函數值都可以通過此索引從表中找到，計算規則見表4。其中，A代表FFT點個數，B代表正弦函數的索引值。

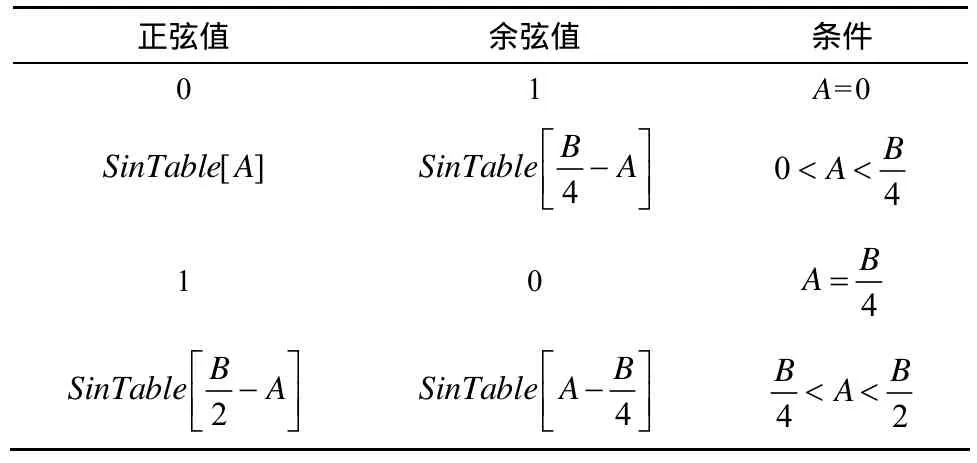
表4 旋轉因子映射公式

SinTable[]的預計算取決于FFT的點數，在本系統中由于采樣頻率（6.144MHz）是固定的，因此對于C/A碼的一個周期（1ms）進行操作，即6144個點，6144不是2的整數冪，但可以拆分為3×211的形式，可以采用一種特殊的FFT算法即PFA算法來進行計算，對于6144點的輸入，PFA算法先進行數據分組，分為3組，然后對3組2048點的數據分別進行FFT運算，最后在進行重新組合，因此旋轉因子表就只針對固定的2048點進行預計算。以下列舉了SinTable[]部分數據。

當在蝶形運算器中需要用到旋轉因子的時候則通過查表的方式從 SinTable[]中得到，正弦函數1/4周期外的數據以及余弦函數的數據，通過表 4中的計算規則獲得，這樣在整個FFT過程中，所有的浮點運算都被轉換為了整數運算，并且在可能的情況下避免乘法運算，除法運算用右移操作來替代，使得運算速度大幅提高。本系統采用 32bit有符號數來存儲蝶形運算中的中間數據，這樣在極端的情況下(32768×6×2048)也不會出現數據越界。

4 算法分析與測試結果

4.1 運算效率分析及結果

對于一個N點DFT，其中的復數乘法次數為N2，而對于一個N點FFT，其復數運算次數為

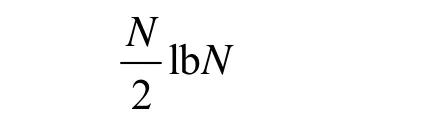
當N的值越大的時候，FFT的加速效果越顯著，每次復數運算可以被拆分為4個浮點乘和6個浮點加運算，在6144點的常規FFT中，浮點乘運算個數為（3×1024×11×4=135168），浮點加運算個數為（3×1024×11×6=202752），計算旋轉因子需要的三角運算個數為（3×1024×2=6144），浮點乘運算個數同樣為（3×1024×2=6144）。本算法將 FFT存在的大量浮點運算全部轉化為了整數運算，并且通過預存正弦函數表的方法省掉了計算旋轉因子的時間，其中，蝶形運算中存在的一些不必要的乘運算可以被省掉，當乘法兩邊存在零值的時候便直接將結果置為零，當乘法兩邊存在一的時候則保存原始數據作為結果，具體操作中會對數據兩邊的值進行檢測，以確定時候符合條件，這樣復數乘法的次數將減少:

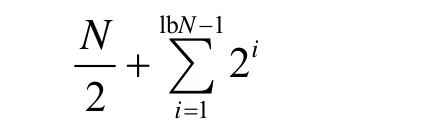
其中，N為FFT點個數。本系統采用2種類型的數據做了測試，一種為采樣率4.096MHz的模擬數據，一種為真實接收的導航數據，重采樣率為6.144MHz，測試平臺為雙核1.83GHz PC，操作系統 Ubuntu-Linux，重復 50次實驗，對結果進行了平均，將本算法跟定點運算和浮點運算做了比較，算法的性能如圖2所示。

文獻[6]中采用的方法是利用特殊軟件相關器的方法，使用并行位操作來實現 32個點同時工作來模擬硬件相關器，其效率有很大程度的提高，但是其實施方式依然是采用循環相關的方式，與本文中采用的位操作結合整數化PFA算法做了對比，如圖3所示。

可以看出由于并行位操作的循環相關運算方式，使得捕獲耗時跟處理數據量成正比關系，而優化PFA算法的本質是FFT運算，PFA的運算量不會隨著處理數據量的成倍增大而過快的增長，因此在長時間累積的情況下有著明顯的優勢。

4.2 資源節省效率分析及捕獲結果

導航數據采取2bit存儲的方式，在捕獲階段，為了提高靈敏度，需要做一個較長時間的累積[12]，本系統采用了 7ms的非相干累積，內存消耗量為（7 × 6144× 2 × 2/8 = 21504）byte，用字節形式存儲相比，2bit方式資源占用量減少75%。在基帶混合階段，原始的復數信號是由2個浮點數組成的，內存消耗量為（21× 6144 × 2× 4 = 1032192）byte，以及相應數量的中間結果存儲，本系統采用了通過表1和表2這2個表位運算的方式來得到表3的索引，以查表的方式來得到結果，因此省去了所有的浮點數存儲空間，內存開銷僅為3個表中的數據，可以忽略。在軟件接收機的跟蹤階段，需要跟蹤并處理相當長的數據，本方法對于資源的節省效率更加突出，尤其在嵌入式設備上，資源的效率顯得更為重要。

本文的實驗平臺采用 Linux-Ubuntu 系統，Intel雙核2.8處理器PC機，實驗數據采用北京回龍觀地區的實地接受信號。對浮點運算和整數運算2種方式得到的捕獲結果做了分析，圖4為浮點運算結果，圖5為本系統采用的整數化方法得到的結果。實驗數據采用信噪比大約為?15dB的實地接收信號，由實驗結果可以看出，對于載波以及旋轉因子的量化并未對捕獲的精度造成很大影響，而速度得到了大幅提升。

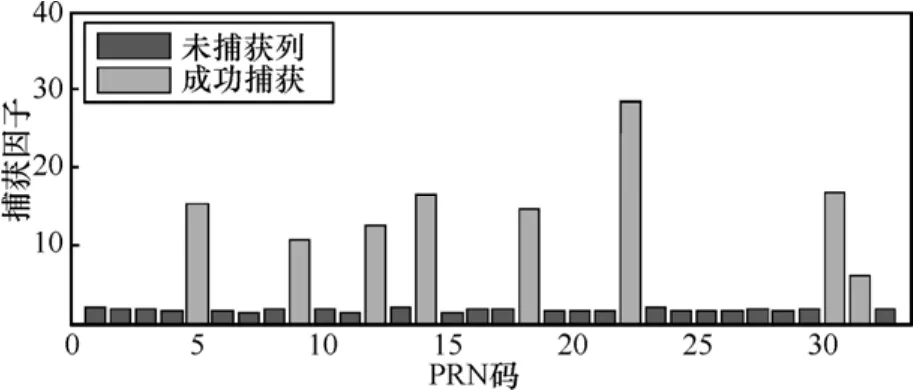
圖4 浮點運算方式的捕獲結果

圖5 整數化方法的捕獲結果

4.3 量化級別與靈敏度分析

本地載波的量化級別會影響到捕獲靈敏度，實驗中采取2bit、4bit、8bit、16bit的量化方式分別對信噪比不同的導航數據進行了測試，對于捕獲結果以及捕獲時間進行了對比，實驗結果如圖6所示。

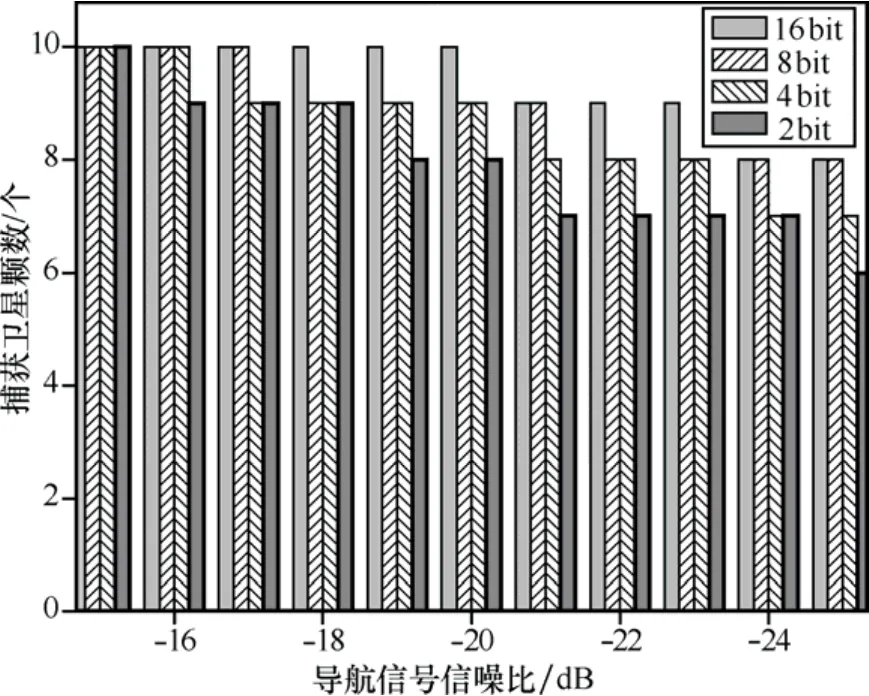
圖6 不同量化級別的捕獲結果

由實驗可以看出當量化等級高的時候在同一信噪比下捕獲到的衛星數量比較多，量化等級低的時候隨著信噪比的降低，會出現丟星的情況，但是在信噪比為?25dB的情況下2bit量化仍然能夠捕獲到6顆衛星，達到了位置解算的要求。在實際的應用中，常常設定一個參數來衡量衛星是否被捕獲到，此參數的值為循環累積的最大值與次大值的比值，比值越大說明相關峰越明顯，再根據此參數與閾值的比較來判斷捕獲結果，在本實驗中發現，2bit與4bit量化方式下，捕獲參數隨著信噪比的下降而降低的比較明顯，信噪比每下降 5dB，捕獲參數大約降低 22.5%，當信噪比非常低的情況下，參數值衰減比較大從而低于閾值而被判為未被捕獲到，而高量化等級的方式下參數值隨信噪比降低而衰減的幅度比較小。因此，可以根據實際情況來選取量化的級別，信噪比高的時候選擇2bit或者4bit的方式，信噪比低的時候選取8bit或者16bit或者更高級別的量化方式，這樣在提高捕獲效率的同時保證了系統靈敏度的需求。

5 結束語

本文的重點在于提高軟件接收機捕獲階段的效率，考慮到GPS數據的特殊存儲結構，提出了一種使用2bit進行操作的PFA算法。在此方法中包括GPS數據，載波頻率以及FFT算法中的旋轉因子都將被量化為比特類型，FFT中的浮點運算被轉化為整數運算。實驗表明此算法使得存在大量FFT運算的捕獲階段效率得到大幅提升，另外，采用多種量化方法也大大減少了資源開銷，尤其在后續的信號跟蹤階段效果更加明顯。嵌入式軟件接收機的實時化實現一直是一個難題，本算法消除了系統中的絕大部分浮點運算，并且進行了大量的量化操作，在性能以及資源都處于劣勢的嵌入式平臺上將會發揮更大的作用，為嵌入式軟件接收機的實時化奠定了基礎。

[1]AKOS D M.Software Radio Approach to Global Navigation Satellite System Receiver Design[D].Ohio:Ohio University, 1997.

[2]VAN NEE D, COENEN A.A new fast GPS code-acquisition technique using FFT[J].Electronics Letters, 1991, 27(2):158-160.

[3]STARZYK J A, ZHU Z.Averaging correlation for C/A code acquisition and tracking in frequency domain[A].IEEE MWSCAS 2001[C].Dayton, Ohio, 2001.905-908

[4]KWONHUE C, KYUNGWHOON C, TAEJIN J.Adaptive PN code acquisition using instantaneous power-scaled detection threshold under rayleigh fading and pulsed gaussian noise jamming[J].IEEE Trans Commun, 2002, 50(8):1232-1235.

[5]CHUANG M Y, FENG K T.Adaptive GPS acquisition technique in weak signal environment[A].IEEE Vehicular Technology Conference[C].Melbourne, 2006.1612-1616.

[6]BRENT M, LEDVINA, MARK L, et al.Bit-wise parallel algorithms for efficient software correlation applied to a GPS software receiver[J].IEEE Transactions on Wireless Communications, 2004, 3(5):1469-1473.

[7]ANDREW J, VITERB I.CDMA Principles of Spread Spectrum Communication[M].MA:Addison-Wesley, 1995.120-135.

[8]OPPENHEIM A V, SCHAFER R W.Discrete-time Signal Processing,2nd Ed[M].New Jersey:PrenticeHall, Inc, 1999.541-669.

[9]KOLBA D, PARKS T.A prime factor FFT algorithm using high-speed convolution[J].IEEE Transactions on Acoustics, Speech and Signal Processing, 1977,25(4):281-294.

[10]曹志剛, 錢亞生.現代通信原理[M].北京:清華大學出版社, 2006.108-110.CAO Z G, QIAN Y S.The Principle of Modern Communication[M].Beijing:Tsinghua University Press,2006.108-110.

[11]BURRUS C, ESCHENBACHER P.An in-place, in-order prime factor FFT algorithm[J].IEEE Transactions on Acoustics, Speech, and Signal Processing, 1981, 29(4):806-816.

[12]ZIEDAN N I, GARRISON J L.Unaided acquisition of weak GPS signals using circular correlation or double-block zero padding[A].IEEE PLANS,2004 Position Location and Navigation Symposium[C].2004.461-470.