數列性質的探究

◆付 偉

(遼寧本溪市衛生學校)

數列性質的探究

◆付 偉

(遼寧本溪市衛生學校)

若數列{an}是是等差數列，有性質:

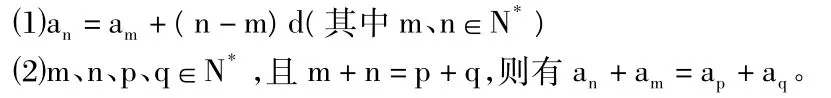
從等差數列的通項公式不難證明這兩個性質，但這僅僅是讓學生在表面上理解這兩個性質，這樣的“傳道授業”，只是生硬地把知識呈給學生，告訴學生結果是什么，卻不能自然地融入到學生已有的認知結構中。因此學生可能會在課堂上模仿運用，課后卻不會獨運用，更談不上靈活了。那么如何根據學生原有的知識與經驗，設計自然的過程，體現學生對等差數列性質的認識過程呢?在教學中我們就利用數軸探究數列的性質進行了研究。

一、緣起

在中學數學里，數軸是常用的工具，它沒有直角坐標系那么豐富多彩，但它本身也是數形結合思想方法的體現。因為它的簡捷方便，使它成為數學解題中最親近的朋友。因為，在數軸上等距離地依次取點，與點對應的一列數便構成了等差數列。

在數軸上任取一點A1，令對應的坐標為a1，然后向右(或向左)每相隔等距離，依次取點 A2，A3…An，并令對應的坐標為 a2，a3，a4，…，an，則得到的一列數a1，a2，a3，a4，…，an，組成等差數列，并且為遞增數列或遞減數列。若設公差為d則有a2－a1=d

于是，我決定利用數軸這位熟悉的朋友，通過問題引導學生的學習活動，這學生鋪設合理的認知臺階;讓學生自己去發現與分析數軸上這些等距離點的關系，從形的關系遷移得到數的關系，進而認識數列中項與項的關系，親身去感受、體驗新知識的形成過程，從而概括得到等差數列的性質。

二、問題與探究

問題一:起點與其它所有點構成的線段有怎樣的關系?

起點與其它點構成的線段分別是 A1A2、A1A3、A1A4…A1An、A1An+1等。

探究1:起點對應的數a1與其它點對應的數之間有怎樣的關系?

因為數軸上兩點間的距離與坐標有如下的關系︱A1An︱=︱an－a1︱;由學生分析探討，得到起點對應的數a1與其它點對應的數之間也有下列關系:

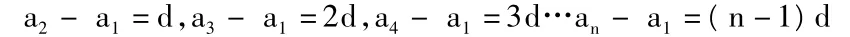
從而得到等差數列的通項公式，既可以拓寬學生的視野，讓學生從形的角度理解通項公式，更可以激發學生發現與得到更多等差數列的性質。

問題二:任意兩點間的線段的長度有什么特點嗎?

任意兩點構成的線段可以是︱A2A4︱、︱A3A6︱、︱AmAn︱等，這些線段的長度分別滿足:

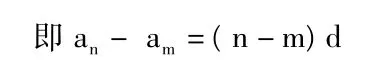
(注:由公差的定義，d的符號由后面項與前面項的差的符號決定，因此d的符號與an－am的符號一致。)

由此，得到等差數列任意兩項間的關系:an－am=(n－m)d

即:等差數列的任意兩項的差就是這兩項的序號的d倍。

移項得an=am+(n－m)and(其中m、n∈N*)

這是等差數列的一個重要遞推式。由這個遞推式，對于一個等差數列{an}，只要給定任

意一項an與公差d，不必去求解首項，可直接寫出該數列的通項。借助數軸，能使學生直觀理解這一性質，加深記憶，真正掌握這個遞推式，也才能使學生在解題時信手拈來，靈活應用。

在學生思維的最近發展區內提問是讓學生自主探究的關鍵。以上關于數軸上點的問題的設計，目的在于讓學生通過觀察與思考去發現一些本來就存在的規律，進一步觀察，可以發現更高層次的規律。

問題三:從“等距離”思考，點與點之間有無其它特殊關系呢?

因為我們在數軸上所取的各相鄰點是等距離的，那么從“等距離”考慮，點與點之間有無其它特殊關系呢?任取點Ak，則點Ak前后兩點分別為Ak－1與 Ak+1，且點 Ak為線段 Ak－1Ak+1的中點，即 Ak－1與 Ak+1關于 Ak對稱;進一步可以發現關于點Ak對稱的點有許多對，它們分別在點Ak的兩側，且與點 Ak等距離。例如:Ak－2與 Ak+2，Ak－3與 Ak+3，…，它們滿足:

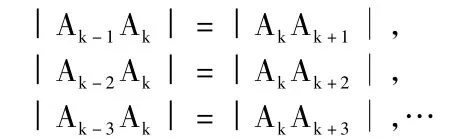
在這個過程中，學生發現，幾乎所有的點都可以作為另外兩點的對稱中心(除了起點與最末的點)幾乎所有的點都能找到關于該點對稱的點。

這種發現激發了學生的興趣，原來不斷地探索，一些規律就在不經意間找到了。

探究3:剛才的發現能否遷移到數列呢?

鑒 于 前 面 的 經 驗，由︱Ak－1Ak︱=︱AkAk+1︱得︱A1Ak︱－︱A1Ak－1︱ = ︱A1Ak+1︱ － ︱A1Ak︱，

即 2︱A1Ak︱ = ︱A1Ak－1︱ + ︱A1Ak+1︱，

把上面等式轉化成對應的數的等式，可得

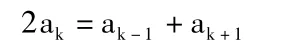
同理可得2ak=ak－2+ak+2;

觀察等式的特征，其中的下標滿足關系

若取k=3，則應有2 a3=a2+a4=a1+a5。

顯然，由通項公式容易證明等式成立。

繼續探討，k=5，是否有2 a5=a1+a9=a2+a8=a3+a7=a4+a6?

探究4:由以上結論，能否推廣到一般呢?

由探究3，學生能自如地寫出下列結論:

此時，很多學生對等差數列中即將出現的又一個特殊性質也是望眼欲穿，雖然有的學生還不會正確地表達出來，但差不多是呼之即出:

若 m、n、p、q 為整數，且滿足 m+n=p+q，則對應的以 m、n、p、q 為下標的項應滿足關系式an+am=ap+aq。

三、后記

經歷了從形到數，從特殊到一般的轉化，學生對這個性質的理解是水到渠成，而且，對這個性質與眾不同的對稱特點印象深刻，于是可以很自然地稱之為數列的對稱性。數列的對稱性揭示了數列內在的規律，顯示了數學的簡潔美。

［1］高中數學課程標準教師讀本.華中師范大學出版社，2003，10.