基于神經網絡結合遺傳算法的Jiles-Atherton磁滯模型參數計算

李慧奇，楊延菊，鄧聘

（華北電力大學河北省輸變電設備安全防御重點實驗室,河北保定071003）

Jiles-Atherton磁滯模型[1]是目前最為常用的描述鐵磁性材料磁滯特性的經典數學模型，是一種具有物理基礎的現象學模型，該模型具有清晰的物理意義，能夠真實的描述B-H的非線性關系，通過求解Jiles-Atherton磁滯模型方程便能夠得到較為準確的B-H磁滯回線，而對Jiles-Atherton磁滯模型參數的辨識是整個問題的關鍵，目前還沒有一種快速的、便捷的、精確的方法對這一問題進行完整的解決，基于此，本文進行研究，通過對原始模型的改進，提出一種新型的算法，即神經網絡結合遺傳算法的方法來解決這一問題。用非線性函數的輸入輸出數據訓練BP神經網絡，預測函數輸出，遺傳算法用于極值尋優，尋找函數的全局最優值及對應的輸入值。

1 改進的Jiles-Atherton磁滯模型

Jiles-Atherton磁滯模型是一種源于磁滯物理的模型，它是通過考慮疇壁移動及能量平衡原理來得到磁化強度與磁場強度的關系方程。物理學家D.C.Jiles和D.L.Atherton通過對疇壁移動機理的研究，推導出描述不可逆微分磁化率和可逆微分磁化率的微分方程。

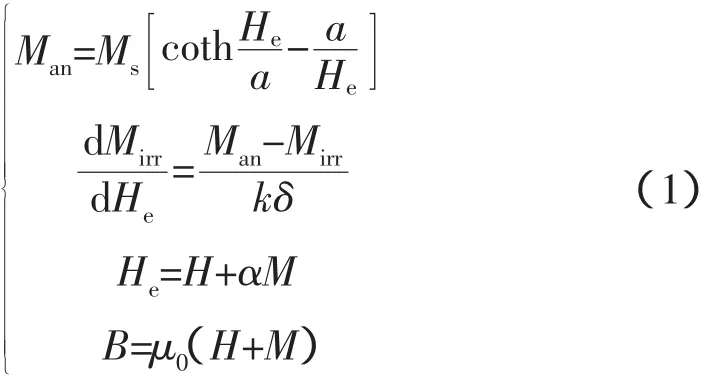
式中，a、α、c、k和飽和磁化強度Ms是由測量磁滯特性所決定的參數；δ是是方向參數，當d H/d t＞0時，其值取+1，d H/d t＜0時，其值取-1。這樣,磁化強度M就能由磁場強度H求解得到。

經典的Jiles-Atherton磁滯模型在使用上有所不便，將對原始的Jiles-Atherton進行形式的改變，改進的模型的主方程[2-3]為

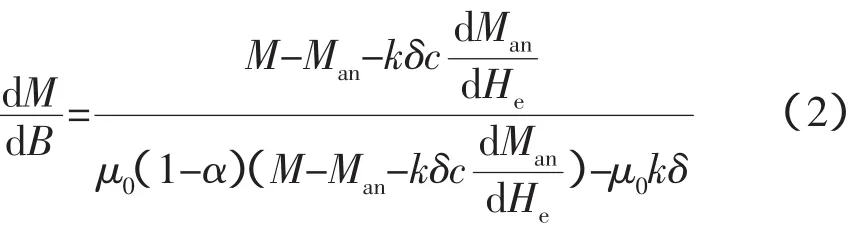
2 BP神經網絡和遺傳算法

BP神經網絡是一個多層的前饋神經網絡，其學習過程由信號的正向傳播與誤差的反向傳播2個過程循環進行的。BP神經網絡是一種多層前饋神經網絡，該網絡的主要特點是信號前向傳遞，誤差反向傳播[7]。在前向傳遞中，輸入信號從輸入層經隱含層逐層處理，直至輸出層[4-9]。每一層的神經元狀態只影響下一層神經元狀態。如果輸出層得不到期望輸出，則轉入反向傳播，根據預測誤差調整網絡權值和閾值，從而使BP神經網絡預測輸出不斷逼近期望輸出。權值的不斷調整過程就是網絡的訓練過程。訓練樣本數據可以是經過分析計算的解，也可以是依據經驗的數據，或為設計過程中產生的計算數據。理論分析已經證明，具有2個隱含層的BP神經網絡進行目標函數映射時，可采用相對簡單的BP神經網絡結構[8]。不過，僅僅使用BP網絡映射優化對象的輸入輸出關系，優化搜索仍沿用傳統算法，還不能完全發揮BP神經網絡的優勢，此時，遺傳算法可成為其重要的補充[9-10]。

遺傳算法是1962年由美國Michigan大學Holland教授提出的模擬自然界遺傳機制和生物進化論而成的一種并行隨機搜索最優化方法。它把自然界“優勝劣汰，適者生存”的生物進化原理引人優化參數形成的編碼串聯群體中，按照所選擇的適應度函數并通過遺傳中的選擇、交叉和變異對個體進行篩選，使適應值好的個體被保留，適應值差的個體被淘汰，新的群體既繼承了上一代的信息，又優于上一代。這樣反復循環，直至滿足條件。遺傳算法提供了一種求解復雜系統優化問題的通用框架，不依賴于問題的具體領域，對問題的種類有很強的魯棒性，所以廣泛應用于函數優化、組合優化、生產調度問題、自動控制、圖像處理機器學習等領域[11]。遺傳算法雖然對于尋優問題有很好的自適應優化能力，但是它不具備自適應學習能力，難以單獨有效地作為一種控制方法研究，但由于遺傳算法能夠收斂到全局最優解，且遺傳算法的魯棒性強，將遺傳算法與神經網絡融合起來不僅能發揮神經網絡的泛化映射能力，而且使神經網絡具有很快的收斂性以及較強的學習能力[12-13]。

遺傳算法具有全局搜索的特性且不依賴梯度信息，也不需要求解函數可微，只需要求解函數在約束條件下可解，用它優化神經網絡的連接權和網絡結構，可以較好地克服BP神經網絡的問題并且有效提高神經網絡的泛化性能。遺傳算法和神經網絡的融合對于尋求全局最優解其效果要優于單個的使用遺傳算法或神經網絡[14-15]。

3 算法的實現和計算結果

3.1 算法原理

遺傳算法優化神經網絡函數極值尋優主要分為BP神經網絡訓練擬合和遺傳算法極值尋優2步，遺傳算法應用于神經網絡是用來函數極值尋優。

神經網絡結合遺傳算法函數極值尋優的算法流程圖如圖1所示。神經網絡訓練擬合根據尋優函數的特點構建合適的BP神經網絡，用非線性函數的輸入輸出數據訓練BP神經網絡，訓練后的BP神經網絡就可以預測函數輸出。遺傳算法極值尋優把訓練后的BP神經網絡預測結果作為個體適應度值，通過選擇、交叉和變異操作尋找函數的全局最優值及對應輸入值。

3.2 計算結果

一般常用的目標函數都是基于最小二乘原理而建立的，由于選用的是磁通密度B為獨立變量，本文建立如下目標函數

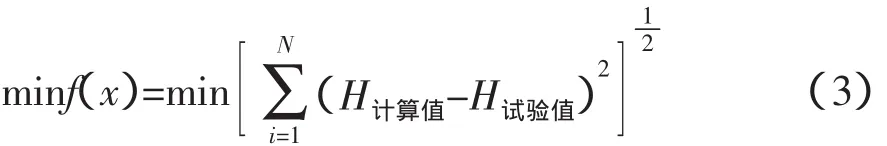
求解上述問題，便能得到所需的5個參數的值（Ms，a，k，c，x）。建立上述目標函數，通過第2節的神經網絡與遺傳算法相結合的極值尋優算法即可求得J-A磁滯模型的5個參數。

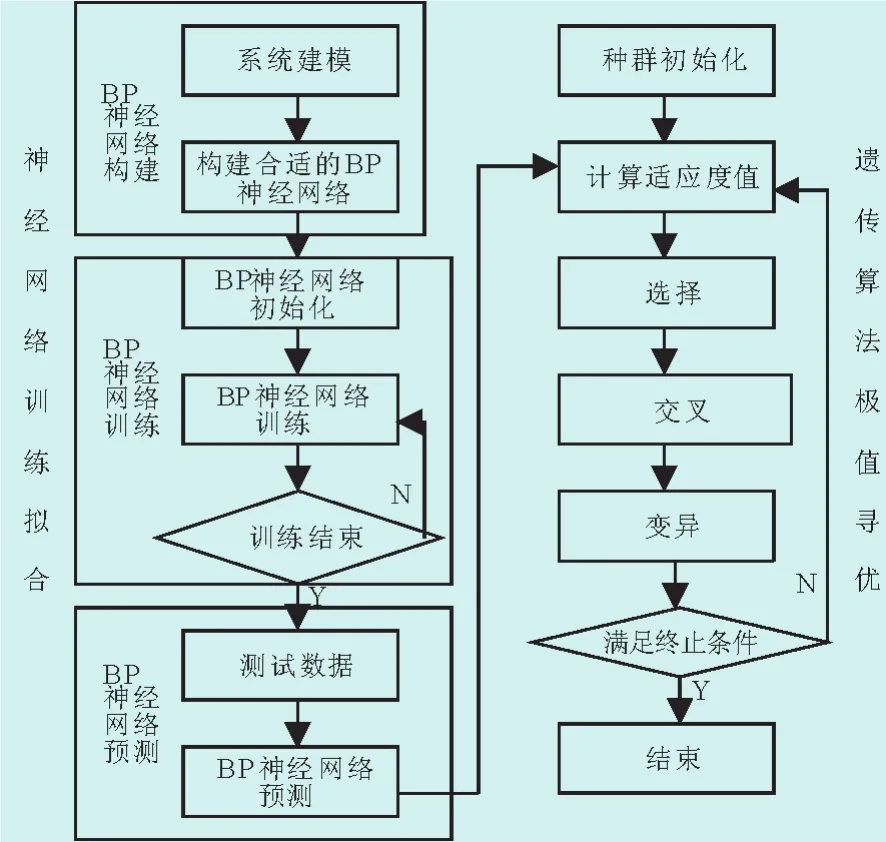
圖1 神經網絡遺傳算法函數極值尋優結構圖Fig.1 Optimization chart of extreme value of the neural network and genetic algorithm function

本文選用30RGH120電工鋼片來進行試驗仿真計算，通過神經網絡與遺傳算法相結合的極值尋優算法進行求解，得到了各個參數的計算值，以及應用文獻[3]中混合算法所得的計算值的比較如表1所示。

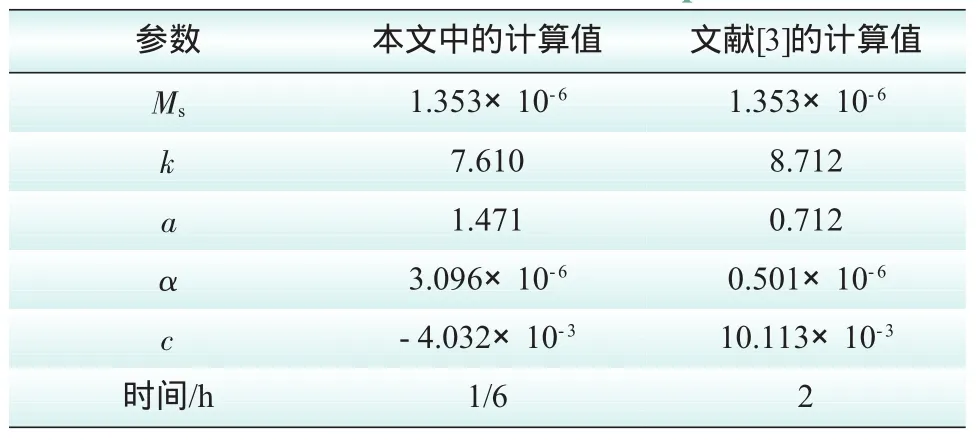
表1 模型參數計算值Tab.1 Calculated value of model parameters

將表1中的參數代人式（2）中，得到了表2中參數所描述的磁滯回線，如圖3所示，得到文中計算值的磁滯回線的計算結果和實驗結果比較圖，如圖4所示，得到文獻[3]中計算值的磁滯回線的計算結果和實驗結果比較圖。

由表1可以看出，應用本文中方法求參數所用的時間要比應用文獻[3]中方法求參數所用的時間少很多，運行速度非常快。由圖2和圖3可以看出，應用本文中方法計算得到的磁滯回線和實驗磁滯回線較為吻合，要比文獻[3]中計算得到的磁滯回線和實驗磁滯回線吻合的好。

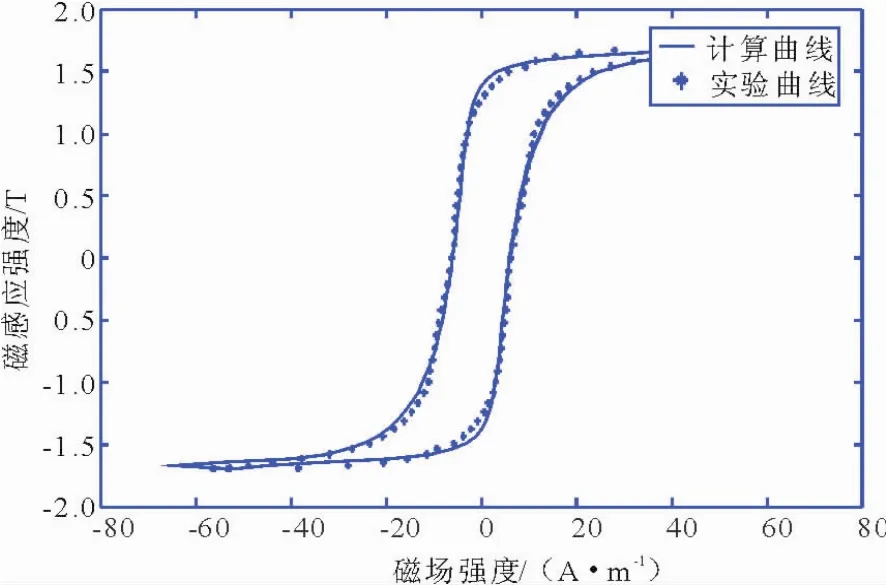
圖2 磁滯回線的計算結果和實驗結果比較圖Fig.2 Comparison charts of the calculation and experimental results of the hysteresis loop

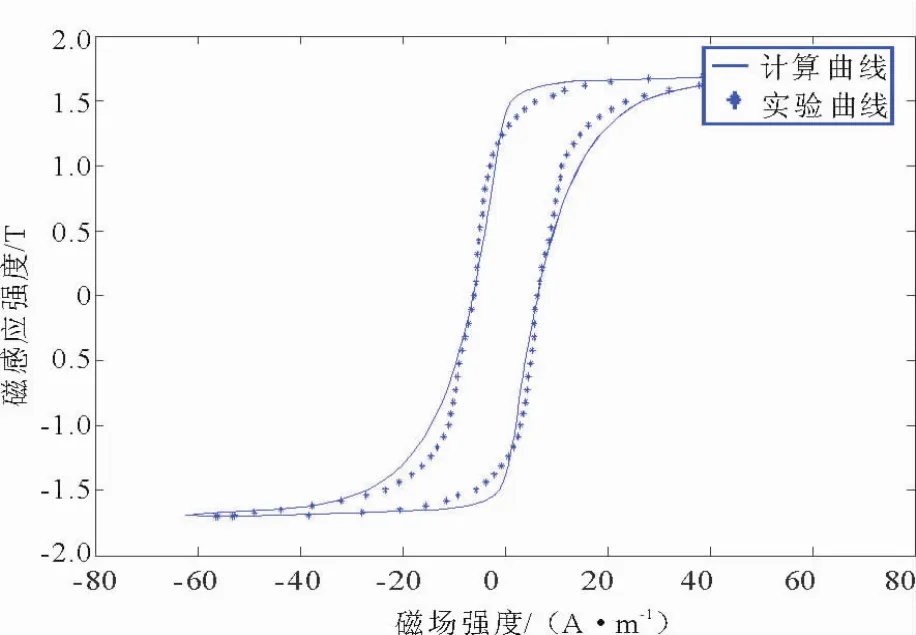
圖3 文獻[3]中磁滯回線的計算結果和實驗結果比較圖Fig.3 Comparison charts of calculation and experimental results of the hysteresis loop in the reference[3]

綜上所述，神經網絡結合遺傳算法函數極值尋優的方法提取Jiles-Atherton磁滯模型得到的參數能夠使計算的磁滯回線和實驗的磁滯回線較好地吻合，此算法求解速度快，精度高，適合非線性程度較高且計算量較大的非線性模型參數的辨識問題。

4 結語

通過以上分析可知Jiles-Atherton磁滯模型的參數的辨識是此模型的關鍵，本文提出了一種較完善的、自動的、精確的方法，來辨識磁性材料的Jiles-Atherton磁滯模型的5個常規參數，此方法求解精度高，速度快，適合非線性程度較高且計算量較大的非線性模型參數的辨識問題，文中方法計算得到的參數能夠使計算磁滯回線與實驗磁滯回線較好地吻合。

[1] JILESD C,THOLKEJ,DEVINE M.Numerical determination of hysteresis parameters for the modeling of magnetic properies using the theory of ferromagnetic hysteresis[J].IEEE Transactions on Magnetics,1992,28(1):27-35.

[2] LI Huiqi,LI Qingfeng,XU Xiaobang,et al.A Modified Method for Jiles-Atherton Hysteresis Model and Its Application in Numerical Simulation of Devices Involving Magnetic Materials.IEEE Transac-tions on Magnetics,2011,47(5):1094-1097.

[3] LI Hui-qi,LI,Qing-feng ZHANG Jun-jie.Calculation of Jjiles-atherton hysteresis model’s parameters using mix of chaos optimization algorithm and simulated annealing aslgorithm.ICMTCE2009[C].Beijing Institute of Technology,2009:11.

[4] 回敬,律方成.將具有可信度的BP神經網絡應用于變壓器故障診斷[J].電力科學與工程,2010,26（2）:9-13.HUI Jing,LüFang-cheng.Application of BP ANN with credence for transformer fault diagnosis[J].Electric Power Science and Engineering,2010,26（2）:9-13(in Chinese).

[5] 張宏亮,吳杰康,陳國通,等.基于神經網絡的短期負荷預測與誤差糾正算法[J].電力科學與工程,2008,24（1）:5-9.ZHANGHong-liang,WUJie-kang,CHEN Guo-tong,et al.Neural network based method for short-termload forecasting and error correction[J].Electric Power Science and Engineering,2008,24（1）:5-9(in Chinese).

[6] 孫娜.基于CMPSO-BP算法的變壓器故障診斷[J].電力科學與工程,2010,26（4）:24-27.SUN Na.Power transformer fault diagnosis based on modified CMPSO-BPalgorithm[J].Electric Power Science and Engin-eering,2010,26（4）:24-27(in Chinese).

[7] 于猛，陳堯隆，梁娟.基于BP神經網絡的碾壓混凝土壩溫度場反分析[J].電網與水力發電進展，2008,24（4）:59-62.YUMeng,CHENYao-long,LIANGJuan.Inverse-analysis method of temperature field on RCC dams based on BP artificial neural network[J].Power Systemand Clean Energy,2008,24（4）:59-62(in Chinese).

[8] 朱凱，王正林.精通MATLAB神經網絡[M].北京：電子工業出版社，2010.

[9] 李慧玲，李春明.一種基于遺傳算法和神經網絡的故障診斷方法[J].電力科學與工程,27（4）:43-47.LI Hui-ling,LI Chun-ming.Artificial neural network classifier usinggenetic algorithmin power electronic circuit fault diagnosis[J].Electric Power Science and Engineering,27（4）:43-47(in Chinese).

[10]馬萌萌，董澤.GA-BP模型在煤質分析中的仿真研究[J].電力科學與工程,2011,27（6）:42-46.MA Meng-meng,DONG Ze.Simulation study on GA-BP model in coal nature analysis[J].Electric Power Science and Engineering,2011,27（6）:42-46(in Chinese).

[11]唐桂花，王加慶.基于基于遺傳算法的水電廠自動發電控制研究[J].電力科學與工程,2007,23（3）:27-29.TANGGui-hua,WANGJia-qing.Study on AGCof hydropower station based on genetic algorithm[J].Electric Power Science and Engineering,2007,23（3）:27-29(in Chinese).

[12]周明，孫樹棟.遺傳算法原理及其應用[M].北京：國防工業出版社，1999.

[13]段新會,王學良,張海俠,等.遺傳算法在過程控制參數擬合中的應用[J].電力科學與工程,2010,26（10）:47-50.DUAN Xin-hui,WANGXue-liang,ZHANGHai-xia,et al.Application of an genetic algorithmin parameter fitting of process control[J].Electric Power Science and Engineering,2010,26（10）:47-50(in Chinese).

[14]李敏強，徐博藝，寇紀淞.遺傳算法與神經網絡的結合[J].系統工程理論與實踐，1999,17（4）:37-40.LI Min-qiang,XU bbo-yi,KOU Ji-song.Combination of genetic algorithms and neural neworks[J].System Engineering Theory and Practice,1999,17（4）:37-40.

[15]ZOU Cheng-ming,Tong Qi Wei,Yang Hong Yun.A study on Neural Network Based on Contractive Mapping Genetic Algorithm[C]//Guo Qingping.International Sysposium on Distributed Computingand Application to Business,Wuhan,2004:777-779.