環境溫濕度與組合梁頻率變化的回歸分析

張金霖

(福建船政交通職業學院，福建福州350007)

橋梁健康監測系統也被稱為風和結構健康監測系統，它利用在橋梁建設時期預埋在橋梁內部關鍵部位的各種應變計、測力計、溫濕度計、風速儀以及疲勞計等傳感器來對橋梁的使用壽命期間的結構健康狀況和性能進行在線監測［1]。通過近幾年在結構健康監測中的研究表明，環境改變對結構動力特性的影響在很多情況下表現顯著，有時甚至可以淹沒許多結構損傷所引起的變化，足以讓決策者做出相反的結論。通過對環境改變中非荷載因素的研究表明，溫度、風力、降雨和濕度都對特征頻率有影響［2－3]。其中，溫度是最主要的影響因素，環境溫濕度與橋梁動力特性的關系并不是確定的函數關系，但是它們之間又確實存在著某種相關關系。要得到它們之間確切的相關關系就必須借助數理統計回歸分析方法［4]。本文以兩跨鋼－混凝土組合梁模型為背景，實測了它們的動力特性及環境溫濕度，應用數理統計回歸分析的方法初步考察了環境溫度變化與橋梁動力特性變化之間的相關性。

1 鋼－混凝土組合梁環境振動試驗

如圖1所示:兩跨鋼－混凝土組合梁跨度各為5 m，鋼梁為10號工字鋼，上翼緣焊接一排栓釘后現澆一層200 mm×80 mm的普通鋼筋混凝土板。組合梁直接安放在支座的滾軸上，支承均為簡支。在支座與跨中的混凝土板內預埋了5個基康溫度傳感器，用以測量混凝土內部溫度以及溫度分布情況。該組合梁模型直接位于實驗室外側，受到陽光和風雨的直接作用，除自重外，梁上沒有任何附加荷載，可以很好地模擬橋梁所處的環境情況。采用環境振動測試模型梁的動力特性，豎向、橫向和縱向的采樣頻率均為600 Hz，濾波400 Hz，每次采樣時間為10 min。組合梁具體尺寸、預埋件位置及測點布置如圖2所示。

選擇典型天氣條件對組合梁進行測試，重點研究環境溫度與濕度對組合梁動力特性的影響。經過近一年的跟蹤監測，可以得到近500次有效數據。這些數據包含組合梁前8階(橫向共4階、豎向共3階、縱向共1階)的動力特性(頻率、振型、阻尼比)，以及同時間采集的環境溫度、環境濕度、梁內各測點的溫度和組合梁的跨中撓度、長度伸縮量。

2 環境溫濕度與組合梁頻率的回歸模型

環境溫濕度與橋梁動力特性之間存在著某種相關關系，要得到它們之間確切的相關關系就必須借助數理統計回歸分析方法［4]。

2.1 二元一次回歸模型

二元正態線性回歸模型的回歸函數的估計為

現在分析環境溫濕度與頻率的回歸關系，即式(1)中，y表示頻率(ω);x1表示溫度(t)，x2表示濕度自然對數值(1nRH)。結果如表1所示。二元一次回歸中，環境溫濕度都能與各階頻率顯著回歸。其中，橫向和縱向的相關系數比較高，可以達到0.75以上，但是豎向的回歸相關系數普遍偏低，最高僅0.52。這個結果還不能令人滿意，于是本文進行了進一步的非線性回歸。

2.2 二元二次回歸模型

由于預先并不知道確切的環境溫度和環境濕度的關系，以及它們與頻率的關系，所以優先選擇運用多項式進行回歸。如表2所示，二元二次回歸已經可以使各階頻率與環境溫濕度的回歸達到較好的效果。

二元二次正態回歸模型的回歸函數的估計為

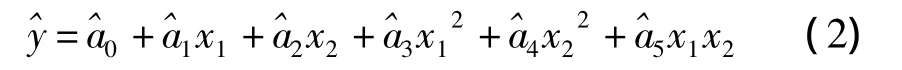
其中公式中各參數的意義同前所述。現在分析環境溫濕度與頻率的二元二次非線性回歸關系，數據分析結果如表2所示。

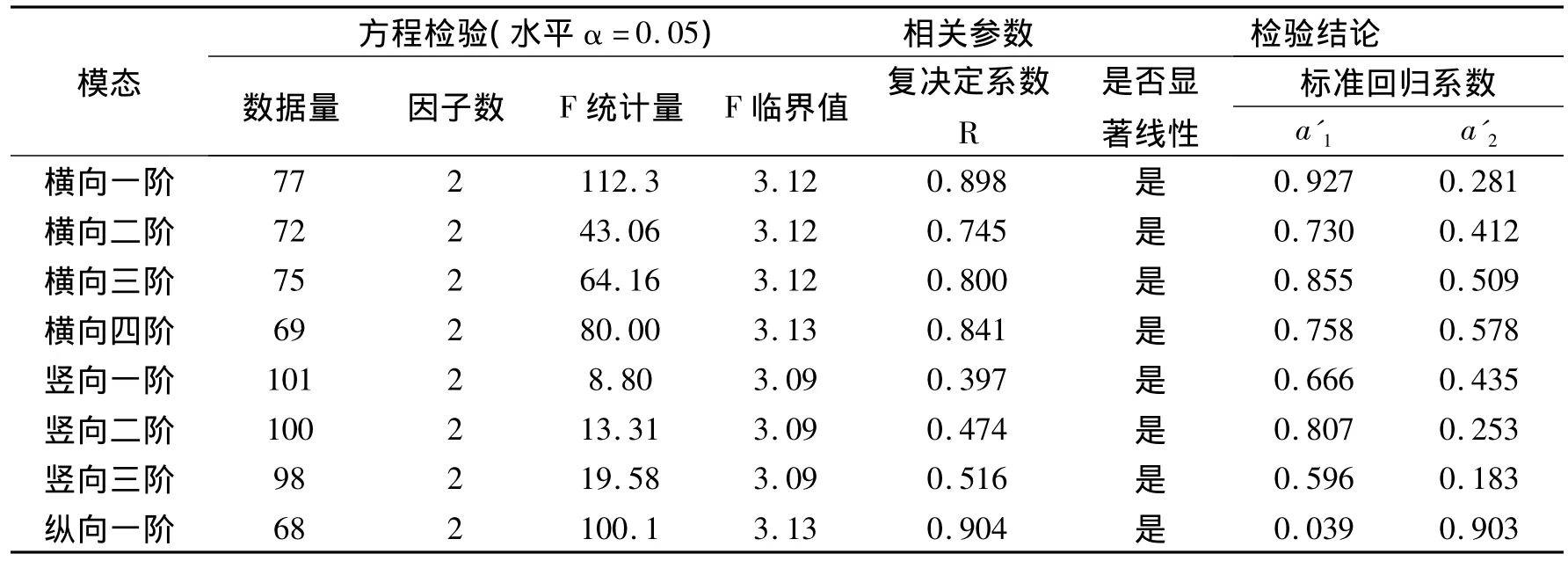
表1 環境溫濕度對頻率的二元一次線性回歸Tab.1 The dual linear regression of the environmental temperature and humidity on the frequency

可以看到，各階模態的相關系數均有較顯著的提高，其中提高幅度最大的是豎向各階振動，最低相關系數已從二元一次線性回歸的0.397達到0.54，因此利用二元二次回歸模型可以反映環境溫濕度與組合梁頻率的關系。二元二次的回歸效果之所以顯著提高，主要由于考慮了環境溫濕度各自的非線性因素以及它們的耦合效應對頻率的影響。由此可見，各階頻率特別是豎向頻率與環境溫濕度之間確實存在顯著的非線性關系。

通過二元二次回歸的各變量系數可以發現，這些變量的系數比較凌亂、各變量系數均有正值與負值出現，找不出明顯的規律性。由此，可以更清楚地了解多項式等非線性回歸的一個特點:這類回歸完全為了擬和出更吻合數據的曲線而回歸，不注重實際的物理意義，不考慮各項變量所表示的具體意義。同時，這樣擬和的曲線確實雖然可以使回歸模型與實測數據很好地吻合，但由于多項式等非線性曲線的特點—振動較大、很不穩定，因此較難運用它們來進行結果預測，使用起來并不很方便。

2.3 四元線性回歸模型

選用怎樣的參數變量既可以較全面地反映試驗組合梁內外溫度的不均勻性對其動力特性的影響，同時又能方便試驗測量采集。是一個比較困難的問題。通過文獻［5－6] 比較后本文精心選用兩個新的參數變量加入回歸分析:一個是環境溫度與梁內的平均溫度之差，它反映了隨環境溫度變化，梁內溫度分布的總體情況;另一個是梁內各測點之間溫度不均勻性產生的方差，它反映了梁內溫度分布差異的大小。對于環境濕度的不均勻性影響，考慮到環境濕度與溫度相比對組合梁頻率的影響相對較小，同時在實測時組合梁各位置環境濕度的差異也十分微小，故本文忽略濕度不均勻性的影響，最終采用四元正態線性回歸模型進行環境溫濕度與組合梁頻率關系的分析。

四元正態線性回歸模型的回歸函數的估計為

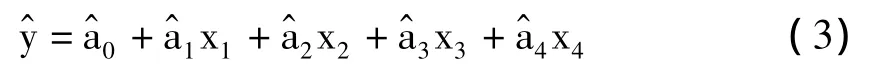
利用式(3)就可以進行環境溫濕度與頻率的四元線性回歸關系分析，令y表示頻率(ω);x1表示溫度(t)，x2表示濕度自然對數值(1nRH)，x3表示梁內各測點溫度不均衡產生的方差值(D(t))，x4表示環境溫度與梁內各測點溫度平均值之差(t環境溫度－t梁內均溫)。很明顯，考慮這兩個參數后回歸效果大大提高，除了能通過假設檢驗外，最低的相關系數也已達到0.62。如表3所示，各參數變量的系數變得更有規律。

表3中，F檢驗的統計量明顯比它的臨界值大，因此所有顯著性檢驗的結果均為“是”。對于相關系數 R，縱向振動為0.92，橫向均在0.7以上，最小為豎向，但也達到0.62以上，這樣的回歸模型已經可以較好反映環境溫濕度對頻率的影響關系。標準回歸系數反映的是各因素在回歸曲線中的影響地位高低。橫向的各階振動中，溫度和相對濕度的自然對數值均處在同一個數量級的影響下，但如果換算為溫度和相對濕度的影響，很明顯，溫度的影響則要比濕度高出40倍左右。溫度不均勻性的影響即a'3+a'4值，與溫度的影響基本處在同一個數量級上，可見，溫度的不均勻性對橫向頻率的影響確實很顯著。再看豎向各階振動，溫度的影響處于最顯著地位，隨后是溫度不均勻性的影響，濕度的影響則最小。有趣的是縱向的規律恰好與豎向相反，濕度自然對數的影響最為顯著，其次是溫度不均勻性，最后才是溫度的影響，但換算成環境相對濕度的影響后，很明顯，濕度對頻率的影響仍低于溫度不均勻性的影響，這再次說明了溫度不均勻性影響的顯著性。

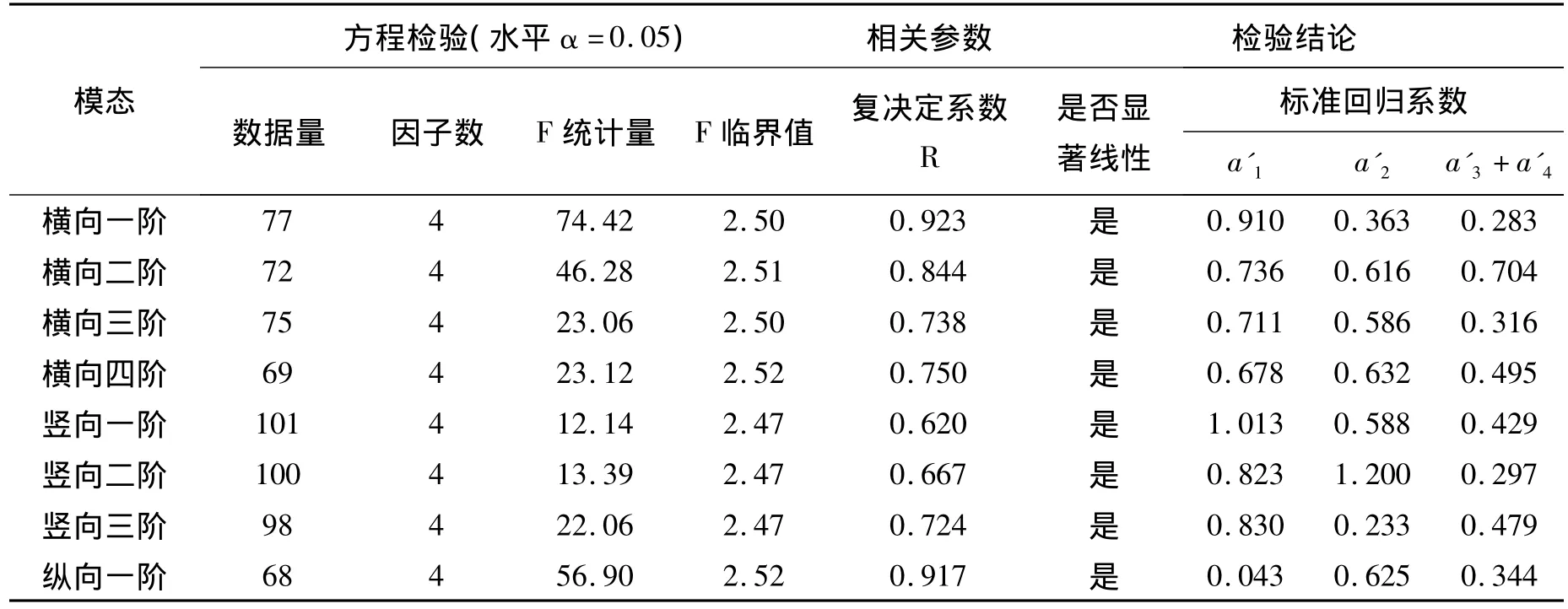
表3 考慮溫度不均勻性時溫濕度與頻率的線性回歸Tab.3 The quaternary linear regression model based on the temperature ununiformity and frequency

表4為三種線性回歸復決定系數值R的比較，可以很清晰的看到，考慮溫度不均勻性時四元線性回歸的復決定系數值R在各個模態情況下較二元一次線性回歸和二元二次線性回歸得到的復決定系數值R都大，表明考慮溫度不均勻性時四元線性回歸結果較好。

3 結論

1)環境溫濕度對組合梁頻率的影響很顯著，但它們之間的關系不是簡單的線性關系，也存在著非線性關系;其中環境溫度變化與組合梁頻率變化呈正相關關系。

2)運用環境溫度與濕度分別及同時與組合梁頻率進行一元及二元線性回歸，無法得到理想回歸效果;進行二元二次非線性回歸，可以得到較理想的回歸效果，但此回歸模型缺乏良好的預測性。

3)溫度不均勻性影響在環境溫濕度與頻率的回歸關系中不能忽略，特別在環境改變劇烈(如溫度驟升或驟降)的情況下將更加顯著。與環境溫度、濕度變量一起與組合梁頻率建立四元線性回歸模型進行回歸分析，此模型較二元二次非線性回歸模型同樣具有良好的回歸效果，同時還擁有良好的預測性。

［1] 于重重，王競燕，譚 勵，等.基于時頻分析方法的橋梁結構健康監測系統［J] .數據采集與處理，2011，26(5):585－591.

［2] 張 通.溫度對大型橋梁模態頻率的影響研究［J] .武漢理工大學學報，2011.33(7):94 －100.

［3] 閔志華，孫利民，仲政.環境溫度對斜拉橋動力特性的影響分析［J] .同濟大學學報:自然科學版，2011，39(4):488－494.

［4] 莊楚強，吳亞森.應用數理統計基礎［M] .廣州:華南理工大學出版社，2004.

［5] 于艷玲.溫度對結構模態頻率影響研究［D] .大連:大連交通大學，2010.

［6] 王立憲.考慮溫度影響下的鋼筋混凝土梁橋的模態參數識別研究［D] .蘭州:蘭州理工大學，2009.