噪聲對維納濾波反卷積算法性能影響的分析*
高明哲 祝明波
(1.海軍航空工程學院研究生管理大隊 煙臺 264001)(2.海軍航空工程學院電子信息工程系 煙臺 264001)
1 引言
掃描體制下的雷達方位回波是由目標方位信息與雷達的天線方向圖函數卷積而成,然而通常在遠距離處的同一距離單元內,會存在兩個或者兩個以上的目標,當天線進行掃描時,在接收機處獲得的回波信號是多目標方位回波的疊加,如果兩個點目標之間的角度間隔小于3dB功率波束寬度,則兩個靠近的點目標不能被分辨[1]。雷達方位超分辨是指將處于同一距離單元內的波束寬度內的幾個目標區別開來的能力。現代戰爭對艦用雷達以及彈載雷達對搜索和識別都提出了更高的要求,因此,提高雷達方位分辨力具有重要的實踐意義。
維納濾波反卷積算法是一種簡單實用的超分辨算法,近來年,運用維納濾波反卷積算法實現雷達的方位超分辨受到了越來越多的關注和研究[2~10]。然而雷達在實際搜索過程中所得到的目標回波必定會有噪聲疊加,這就對反卷積算法的實際應用效果產生了影響。
本文首先闡述了維納濾波反卷積的算法理論,其次利用MATLAB對不同信噪比下維納濾波反卷積算法處理后的雷達回波信號進行了仿真實驗,從而得到信噪比對該算法的超分辨倍數的影響,最后對算法的實用性進行評估。
2 算法理論
維納濾波是利用平穩隨機過程的相關特性和頻譜特性對混有噪聲的信號進行濾波的方法,運用到反卷積問題中可以在最小均方誤差下得到真實信號的最佳估計值。基本原理是[11]:
給定觀測序列y(n),它是一個非因果系統的輸出

式中,ζ(θ)為噪聲。希望找一個非因果濾波器h(θ),它用y(θ)作輸入,使其輸出:
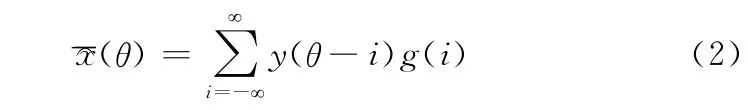
滿足:
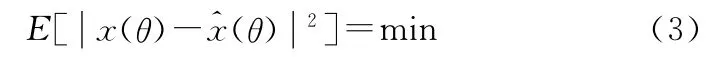
由此得到:

這個式子的離散傅里葉變換給出:

式中,G(ω)是h(θ)的 DTFT。Sxy(ω)和Syy(ω)分別是交叉功率譜和自功率譜。維納濾波器可以表達為

另一方面,由于:

Sxx(ω)和Snn(ω)分別是輸入信號和噪聲的自功率譜。于是維納濾波器可以表示為

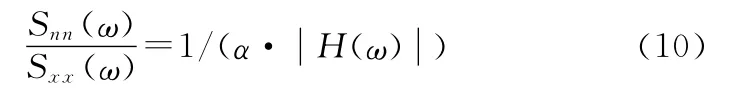
3 仿真分析

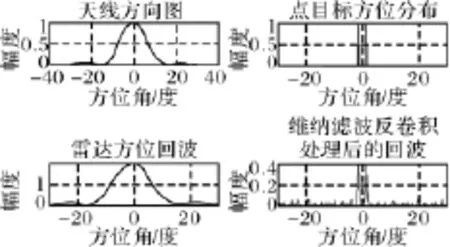
圖1 信噪比為60dB時的情形
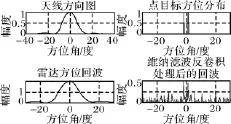
圖2 信噪比為40dB時的情形

圖3 信噪比為20dB時的情形
通過仿真對比可以看出,隨著信噪比下降,維納濾波的超分辨性能同樣也隨之下降,當信噪比降低至20dB時,兩目標不可分辨。
通過仿真實驗得知,常數α可以對噪聲有一定抑制作用,而且對反卷積效果有很大影響。當信噪比較高時,不需要對噪聲有很強抑制,α取之較小,也對去卷積的效果影響較小;而當信噪比較低時,α要取較大值來抑制噪聲,此時α取值越大,則去卷積效果越差。
調整點目標方位向上的間距,使反卷積的結果剛好能分辨出兩個點目標,得到信噪比與維納濾波超分辨倍數的關系如表1所示。

表1 信噪比與維納濾波超分辨倍數的關系
4 結語
由上面的仿真結果可以看出,隨著信噪比的下降,維納濾波反卷積算法的超分辨倍數也隨之下降。在高信噪比時,維納濾波反卷積算法具有較高的超分辨能力,而信噪比降低至20dB以下時,該算法失去作用。因此我們可以根據噪聲環境的不同,選擇恰當的信號處理方法,在高信噪比時采用維納濾波反卷積算法,在低信噪比時采用其他方法,以到達最優的超分辨效果。
[1]丁鷺飛,耿富錄.雷達原理[M].第三版.西安:西安電子科技大學出版社,2003:200-201.
[2]Zhao J,Gaydecki PA,Burdekin FM.Investigation of Block Filtering and Deconvolution for the Improvement of Lateral Resolution and Flaw Sizing Accuracy in Ultrasonic Testing[J].Ultrasonics,1995,33(3):187-194.
[3]單榮光,李士國,朱力.去卷積實現雷達方位超分辨[J].船用雷達與對抗,1994(1):9-13.
[4]郭建中,林書玉.超聲檢測中維納逆濾波解卷積方法的改進研究[J].應用聲學,2005(3):97-102.
[5]李勛,武傳華,許士敏.去卷積提高方位分辨率[J].艦船電子工程,2005(5):50-53.
[6]Daly CJ,Rao NAHK.A Spatially Averaged Impulse Response for An Unfocused Piston Transducer[J].J Acoust Soc Am,1999,103(3):1563-1566.
[7]Zhou Daolin,Huang Yulin,Yang Jianyu.Radar Angular Superresolution Algorithm Based on Bayesian Approach[C]//ICSP 2010Proceedings,2010:1894-1897.
[8]Craig E.Morris,Mark A.Richards and Monson H.Hayes.Fast Reconstruction of Linearly Distorted Signals[J].IEEE Transactions on Acoustics,1988,36(7):1017-1025.
[9]Hutchins DA,Pardoe AC,Billson DR.Neural Network Correction of Ultrasonic C-scan Images[J].Ultrasonics,1999,37(4):263-272.
[10]白文斯密,馬洪.一種利用多核解卷積提高雷達角分辨力的方法[J].電視技術,2008,12,48(12):43-46.
[11]鄒謀炎.反卷積與信號復原[M].北京:國防工業出版社,2001:93-95.

